zaev ea 2
реклама

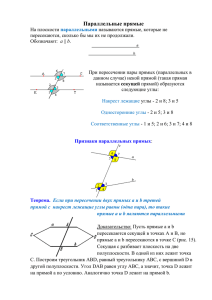
Признаки параллельных прямых Задачи урока знать формулировку признаков параллельности прямых; уметь применять данные признаки при решении задач Две прямые параллельны, если они не пересекаются. а b b a 1 3 2 4 5 7 6 с – секущая 8 c •накрест лежащие углы: 1и8 2и7 3и6 4и5 b a 1 3 2 4 5 7 6 с – секущая 8 c •односторонние углы: 3и5 4и6 1и7 2и8 b a 1 3 2 4 5 7 6 с – секущая 8 c •соответственные углы: 1и5 2и6 3и7 4и8 Признак 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. c a A 1 b 2 Дано: а и b – прямые с - секущая 1=2 B Доказать: а||b •Точка О – середина отрезка АВ, то есть АО = ОВ. •Из точки О проведем перпендикуляр ОН к а. •На прямой b от точки В отложим отрезок ВН1=АН. •1 = 2 по условию. •Соединим точки О и Н1. ∆АНО = ∆ВН1О по двум сторонам (АО=ВО, ВН1=АН) и углу между ними (1=2). •Из равенства треугольников следует, что углы a АОН и ВОН1 равны. •Из пункта 6 следует, что точки Н1, О и Н лежат на одной прямой. •Из равенства треугольников следует, что углы b ОН1В = ОН1В = 90°, так как ОН1В – прямой по построению. •Получаем, что а и b перпендикулярны НН1. По теореме о двух прямых, перпендикулярных третьей, а|| b. c H A 1 O 2 B H1 Признак 2. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. Признак 3. Если при пересечении прямых секущей соответственные углы равны, то прямые параллельны. Задачи урока знать формулировку признаков параллельности прямых; уметь применять данные признаки при решении задач Домашнее задание: вопросы 27 - 28, № 41, № 42