1). - SlideBoom
реклама

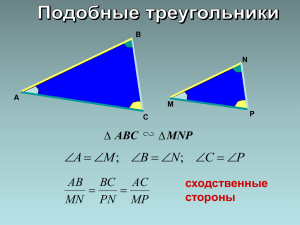
Второй и третий признаки подобия треугольников II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. АВ АС Дано: ABC, А1В1С1, А А1 , А1 В1 А1С1 Доказать: ABC А1В1С1 Идея доказательства: Рассмотрим два треугольника ABC и А1В1С1 . Докажем, что они подобны. Для этого построим треугольник ABC2 и докажем, что он подобен треугольнику А1В1С1 . Рассмотрим треугольники ABC и ABC2 и докажем, что они равны. Сделаем вывод о подобии треугольников ABC и А1В1С1. Доказательство: докажем, что В В1 и применим 1 признак подобия треугольников С1 А1 С В1 А В С С1 В1 А1 В А 1 2 1). Рассмотрим ABC2, у которого 1= А1, 2=В1. ABC2 А1В1С1 по двум углам АВ АС2 Тогда А1 В1 А1С1 АВ АС по условию А1 В1 А1С1 С2 АС = АС2 С С1 В1 А1 В А 1 2 2). ABC = АВС2 В = 2, = по двум сторонам и углу между ними С2 2=В1 Значит ΔABC~ΔA1B1C1 по I признаку подобия. III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. Дано: АВ ВС АС А1 В1 В1С1 А1С1 ABC, А1В1С1, Доказать: ABC А1В1С1 Доказательство: (аналогично) Что нужно рассмотреть, чтобы доказать, что ABC А1В1С1 ? Каким признаком подобия мы воспользуемся? Какой вспомогательный треугольник мы должны рассмотреть? Какому треугольнику он будет подобен? По какому признаку? Если треугольники подобны, то какое отношение мы можем составить? С каким отношением мы должны его сравнить? Что будет следовать? Доказательство: докажем, что А А1 и применим 2 признак подобия треугольников С С1 А1 В1 А В С С1 В1 А1 В А 1 2 1). Рассмотрим ABC2, у которого 1= А1, 2= В1. ABC2 А1В1С1 Тогда по двум углам АВ ВС 2 АС2 А1 В1 В1С1 А1С1 АВ ВС АС по условию А1 В1 В1С1 А1С1 АС = АС2 С2 ВС = ВС2 С С1 В1 А1 В А 1 2 2). ABC = АВС2 А = 1, = по трем сторонам С2 1= АА11 Значит ΔABC~ΔA1B1C1 по II признаку подобия. Решение задач №1 По данным рисунка Найти: x Доказать: BC||AD Решение: 1) Рассмотрим два треугольника с общей вершиной AOD и COB : BOC DOA, так как они вертикальные. Рассмотрим отношение прилегающих сторон: DO AO DO 4 AO 6 2 2 BO CO AO 2 CO 3 Согласно II признаку подобия AOD ~ COB . Коэффициент подобия k=2. С помощью него определим длину x=AD: x 2 | x 2 * BC 2 * 4 8 BC 2) Так как AOD ~ COB, то все углы у них равны. OBC ODA- эти углы являются накрест лежащими при пересечении прямых BC и AD секущей BD. Таким образом, BC||AD. Ответ: 8 №2 По данным рисунка найти длину x, отметить равные углы, доказать, что ABC ~ AB1C1 №3 Подобны ли треугольники ABC и А1В1С1, если АВ = 3 см, ВС = 5 см, АС = 7 см, А1В1 = 4,5 см, B1C1 = 7,5 см, A1C1 = 10,5 см? C C1 AA1 B1 B №4 По данным рисунка докажите, что B1C1 || АC. B A №5 Докажите, что два равносторонних треугольника подобны. B N A C M K №6 По данным рисунка найдите угол K. B M 10 40o 14 5 7 80o A 12 C K 6 P Домашняя работа: из презентации задачи №2, 3, 4, 5, 6 тетрадь-конспект стр. 54 – типовая задача стр. 55 – типовая задача, опорная задача.