ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КОМПЬЮТЕРА ИНФОРМАТИКА

ОСНОВЫ ЛОГИКИ И
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
КОМПЬЮТЕРА
ИНФОРМАТИКА
10 класс
Марковская Наталья Ивановна
МБОУ СОШ № 23
г. Новочеркасск





ЛОГИЧЕСКИЕ ОПЕРАЦИИ
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
ТАБЛИЦЫ ИСТИННОСТИ
ЛОГИЧЕСКИЕ СХЕМЫ
ЛОГИЧЕСКИЕ ЗАДАЧИ
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
 КОНЬЮНКЦИЯ
 ДИЗЬЮНКЦИЯ
 ИНВЕРСИЯ
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
 КОНЬЮНКТОР
 ДИЗЬЮНКТОР
 ИНВЕРТОР
КОНЬЮНКЦИЯ
(ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)
ОБОЗНАЧЕНИЕ
&
В ЕСТЕСТВЕННОМ
ЯЗЫКЕ
и
В ЯЗЫКАХ
ПРОГРАММИРОВАНИЯ
and
А
В
A&B
0
0
0
0
1
0
1
0
0
1
1
1
«На улице светит солнце и идет снег»
ДИЗЪЮНКЦИЯ
(ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)
ОБОЗНАЧЕНИЕ V
В ЕСТЕСТВЕННОМ
ЯЗЫКЕ ИЛИ
В ЯЗЫКАХ
ПРОГРАММИРОВАНИЯ
OR
А
В
AvB
0
0
0
0
1
1
1
0
1
1
1
1
«На улице светит солнце или идет снег»
ИНВЕРСИЯ
(ОТРИЦАНИЕ)
ОБОЗНАЧЕНИЕ
А
В ЕСТЕСТВЕННОМ
ЯЗЫКЕ
НЕ
В ЯЗЫКАХ
ПРОГРАММИРОВАНИЯ
NOT
«Не верно…»
«Не …»
«На улице не светит солнце»
A
A
0
1
1
0
КОНЬЮНКТОР
ВХОД 1
&
ВХОД 2 ВЫХОД
0
0
0
0
1
0
1
0
0
1
1
1
ДИЗЪЮНКТОР
OR
ВХОД 1
ВХОД 2
ВЫХОД
1
1
1
1
0
1
0
1
1
0
0
0
ИНВЕРТОР
NOT
ВХОД
ВЫХОД
0
1
1
0
ЛОГИЧЕСКИЕ СХЕМЫ
ОПРЕДЕЛИТЕ, КАКИЕ СИГНАЛЫ 0 ИЛИ 1 НУЖНО
ПОДАТЬ НА ВХОДЫ, ЧТОБЫ ЗАГОРЕЛАСЬ
ЛАМПОЧКА.
AND
NOT
ЗАДАНИЯ
ТАБЛИЦЫ ИСТИННОСТИ
( 2 * 2  5 или 2 * 2  4 )
(А v B)
ТАБЛИЦЫ ИСТИННОСТИ
2
n
- КОЛИЧЕСТВО СТРОК =
,
n- количество логических переменных
КОЛИЧЕСТВО СТОЛБЦОВ
КОЛИЧЕСТВО ЛОГИЧЕСКИХ
ПЕРЕМЕННЫХ
КОЛИЧЕСТВО ЛОГИЧЕСКИХ
ОПЕРАЦИЙ
УПРАЖНЕНИЯ
СОСТАВИТЬ ТАБЛИЦУ
ИСТИННОСТИ
F = (A v B) & (A v B)
A
B
AvB
A
B
AvB
F
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
ДОКАЖИТЕ, ЧТО
A v (B&C) = (A v B) & (A v C)
A
B
C
B&C
AvB
AvC
Av(B&C)
(AvB)&(AvC)
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
0
1
1
1
1
1
1
0
1
0
1
1
1
1
1
0
0
0
1
1
1
1
1
0
0
0
1
1
1
1
1
ЗАПОЛНИТЕ ТАБЛИЦУ
ИСТИННОСТИ
ФОРМУЛА
ВЫСКАЗЫ
ВАНИЕ
А
Зверь
полосатый
В
Зверь
хищный
ТИГР
ВОЛК
БУРУНДУК
ЗАЯЦ
не А
не В
АиВ
А или В
ОТВЕТ
ПРОВЕРИМ!
ФОРМУЛА
ВЫСКАЗЫ
ВАНИЕ
ТИГР
ВОЛК
БУРУНДУК
ЗАЯЦ
А
Зверь
полосатый
И
Л
И
Л
В
Зверь
хищный
И
И
Л
Л
не А
Зверь не
полосатый
Л
И
Л
И
не В
Зверь не
хищный
Л
Л
И
И
АиВ
Зверь
полосатый
и хищный
И
Л
Л
Л
А или В
Зверь
полосатый
или
хищный
И
И
И
Л
Для решения многих логических задач необходимо:
1) выделить элементарные (простые) высказывания и
обозначить их буквами;
2) записать условие задачи на языке алгебры логики,
соединив простые высказывания в сложные с помощью логических
операций;
3) составить единое логическое выражение для всех требований
задачи;
4) используя законы алгебры логики попытаться упростить
полученное выражение и вычислить все его значения либо
построить таблицу истинности для рассматриваемого выражения;
5) выбрать решение — набор значений простых высказываний,
при котором логическое выражение является истинным;
6) проверить, удовлетворяет ли полученное решение условию
задачи.
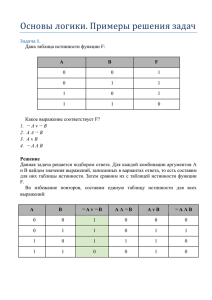
ПРИМЕР 1.
Компьютер вышел из строя (нет изображения на экране монитора), однако
неизвестно какое устройство не работает (монитор, видеокарта или
оперативная память). Можно предположить следующее:
1) Если монитор исправен или видеокарта неисправна, то оперативная память
неисправна;
2) Если монитор исправен, то оперативная память исправна.
Исправен ли монитор?
1. Рассмотрим простые высказывания:
А = {Монитор неисправен},
В = { Видеокарта неисправна},
С = { Оперативная память неисправна}.
2. Запишем на языке алгебры логики наши предположения:
(
В)С и

.
3. Пусть F(A, B, C) = ((
В)С )&(

).
Составим для данного высказывания
таблицу истинности:
4.
В

F
1
1
0
1
0
0
0
1
0
1
1
0
1
1
1
0
0
0
0
0
0
1
1
1
1
0
1
0
1
1
0
1
1
1
1
0
0
1
0
1
1
0
1
1
1
0
1
1
0
1
1
(
В)С
A
B
C
0
0
0
1
1
0
0
0
1
1
1
0
1
0
1
0
1
1
1
0
1
5. Решить данную задачу — значит указать, при каких значениях А
полученное сложное высказывание истинно. Необходимо проанализировать
все строки таблицы истинности, где F = 1. Анализ таблицы показывает, что
сложное высказывание истинно во всех случаях, когда А — истинно, т. е.
вероятнее всего неисправен именно монитор.
Укажите, при каких состояниях
выключателей лампочка будет гореть.
AND
NOT
NOT
AND
NOT
Укажите, при каких состояниях
выключателей лампочка будет
гореть.
NOT
OR
NOT
AND
OR