Полупроводниковые устройства Лекция 15 Весна 2012 г.
реклама

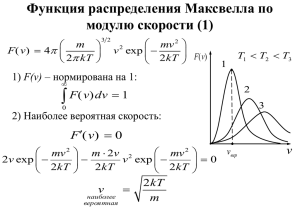
Полупроводниковые устройства Лекция 15 Весна 2012 г. Уже была ранее формула ne N c exp E c E F kT • Или эту же формулу можно представить в виде ne const T 3 2 exp E c E F kT Для собственных полупроводников Ec – EF ≈ Eg/2 E g ne ni const T 2 exp 2kT 3 • Удельная электропроводность собственных п/п: E g 3 i ni e e h const T 2 e e h exp (1) 2kT Зависимость подвижности носителей тока от температуры • Подвижность носителей тока уменьшается с ростом температуры. Это обусловлено, главным образом, рассеянием на кристаллической решетке (с ростом температуры амплитуда колебаний растет). Приближенно эта зависимость описывается соотношением const T 3 2 (2). • На самом деле показатель степени при Т чаще всего имеет значение между −2 и −2.5 Подставим (2) в (1): 0 exp E g 2kT (3) • Коэффициент σ0 не зависит от температуры (T-3/2×T3/2=1) ln ln 0 Eg 2kT (4) p – n - переход Ток через p-n-переход • В общем случае концентрация электронов в зоне проводимости определяется соотношением (распределение Максвелла – Больцмана): n N c exp E c E F kT Соответственно, в p-области перехода концентрация электронов в зоне проводимости равна n p N c exp E cp E F p • В соответствии с рисунком, имеем E1 E cp E F p • Поэтому n p N c exp E1 kT kT Электронный ток из p-области обусловлен дрейфом электронов и пропорционален их концентрации • Отсюда имеем / ie A exp E1 kT / • Аналогично для n-области имеем nn N c exp E 2 kT • C учетом потенциального барьера ΔE сила тока равна ie Aexp E 2 kT exp E kT В условиях равновесия ie/ ie A / exp E1 kT Aexp E 2 kT exp E kT Aexp E 2 E kT что E1=E2+ΔE, поэтому • Из рисунка следует, AA / Теперь для силы тока можно записать, что ie / ie Aexp E1 kT ih ih/ A exp E1 kT • Нижнее уравнение – дырочный ток При наложении внешней разности потенциалов, получим • для тока ie A exp E 2 kT exp E eU kT A exp E 1 kT exp eU kT / ie A exp E1 kT / Результирующий ток равен Ie / ie ie eU / ie exp 1 kT • Аналогично для дырочного тока: I h ih ih/ eU / ih exp 1 kT Теперь полный ток через переход можно записать в виде eU I I 0 exp 1 kT Жорес Алферов Тепловые сопротивления (термисторы) Полупроводники: • Применение в качестве чувствительных термометров при дистанционных измерениях • Использование в качестве термометров для замера температур окружающей среды Термистор(видео – опыт) Фоторезистор Когда на транзистор падает свет достаточно большой энергии, т.е. с достаточно малой длиной волны, в нем освобождаются электроннодырочные пары. Если пары возникают вблизи p-n-перехода с напряжением обратного смещения, они могут диффундировать в область перехода. Один из носителей может быть ускорен напряжением, имеющимся на переходе, и тогда он приобретает способность освобождать дополнительные заряды в процессах столкновения. В материале n-типа ускоряется дырка, в материале p-типа – электрон. Поскольку заряды несут ток через переход, он возникает и во внешней цепи, т.е. свет преобразуется в электрический ток. Фоторезистор Использование: 1. Регистрация и изменения слабых световых потоков. 2. Обнаружение инфракрасных лучей. 3. В автоматических устройствах, служащих для подсчета изделий движущихся на конвейере, контроля их размеров Например, турникет в метро работает именно по такому принципу.