Движение проводника с током в магнитном поле

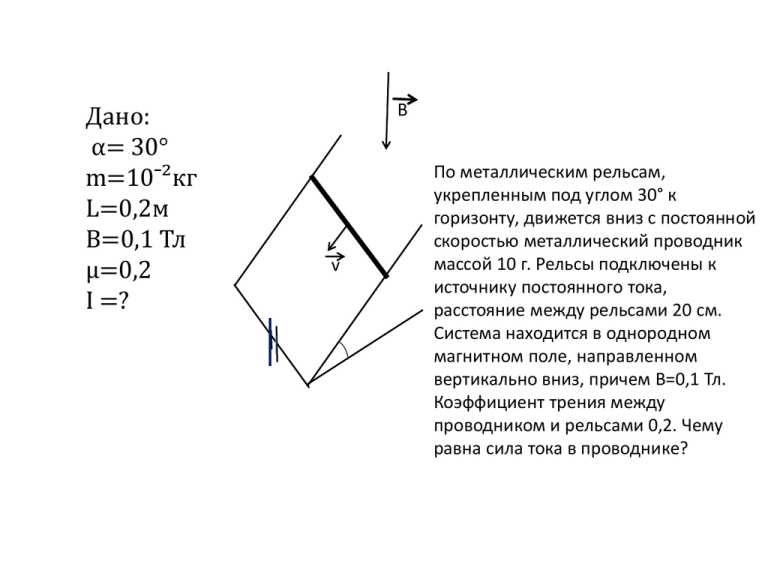
Дано:
α= 30°
m=10ˉ²кг
L=0,2м
В=0,1 Тл
µ=0,2
I =?
В
v
По металлическим рельсам,
укрепленным под углом 30° к
горизонту, движется вниз с постоянной
скоростью металлический проводник
массой 10 г. Рельсы подключены к
источнику постоянного тока,
расстояние между рельсами 20 см.
Система находится в однородном
магнитном поле, направленном
вертикально вниз, причем В=0,1 Тл.
Коэффициент трения между
проводником и рельсами 0,2. Чему
равна сила тока в проводнике?
OX: - mg sin𝛼 + Fтр + Fa cos𝛼 = 0,
OY: -mg cos𝛼 + N - Fa sin𝛼 = 0
Fтр=µN
N = mg cos𝛼 + Fa sin𝛼
-mg sin𝛼 + µ(mg cos𝛼 + Fa sin𝛼) + Fa cos𝛼=0
Fa =
α
Fa = IlB
I=
Ответ: I=1,69 А.
= 1,69A
Задача № 2
•
На горизонтальной диэлектрической поверхности проложены два параллельных
металлических рельса. На рельсах перпендикулярно им лежат два одинаковых
проводника массой 50 г и длиной50 см каждый. Вся система находится в однородном
магнитном поле индукция которого направлена вертикально вверх. Модуль индукции
магнитного поля В=2 Тл, сопротивление каждого проводника 2 Ома, коэффициент
трения между проводниками и рельсами 0,3. Сопротивлением рельсов можно
пренебречь. С какой максимальной скоростью можно перемещать левый проводник
вдоль рельсов, чтобы правый проводник при этом оставался в покое? В какую сторону
будет двигаться правый проводник, если увеличить скорость движения левого
проводника по сравнению с рассчитанным значением? Магнитное поле индукционного
тока мало по сравнению с внешним магнитным полем.
Дано:
m=50г
l=50см
В=2Тл
µ=0,3
𝑣л-?
l
.
Модель
.
Bi
Ei = B𝑣l
Fa≤Fтр max
BIl≤µmg
I=
=
B2𝑣l2 ≤ µmg
2R
𝑣≤
B2 l 2
𝑣max=
B2l2
= 0,6 м/с
Задача № 3
По двум металлическим параллельным рейкам, расположенным
горизонтально и замкнутым на конденсатор ёмкостью С, может без
трения скользить проводящая перемычка массой m. Система
находится в однородном магнитном поле с индукцией В. К середине
перемычки прикладывают горизонтальную силу F в направлении,
указанном на рисунке. Расстояние между рейками L. Считая
сопротивление реек и перемычки малыми, найти ускорение
перемычки.
Дано:
m
C
B
F
l
a-?
X
l
C
φ1-φ2=B𝑣l
𝑣 – скорость движения перемычки
φ1-φ2 = Uc
B𝑣l =
+
X
+
-
l
C
I
Blv´= 1\Cq´
Bl
-
X
=
I=
a=
I = CBla
F – Fa = ma
F – IBl = ma
F – (CBla)Bl = ma
F = CB2l2a + ma
a=
Задача№4
•
Металлический стержень длиной 1м вращается в однородном
магнитном поле с индукцией 0,1 Тл в плоскости, перпендикулярной
линиям магнитной индукции. Ось вращения совпадает с одним из
концов стержня. Частота вращения f = 600 об\мин. Найти разность
потенциалов U на концах стержня.
Дано:
l=1м
B = 0,1 Тл
f = 600 об/мин
X
X
X
X
X
X
U-?
O
1 способ:
E
αl
eE – e𝑣B =
X
X
𝑣 = ωx = 2πfx
eE – e(2πfx)B =
X
X
X
X
E=
E = αx
b = αl
U = φ0 – φl = α
=π
U=π
+
+
b
x
l
=
=
x
Способ 2:
ξi =
∆S
h=α
∆S =
α = 2πf∆t
∆S = πfl2∆t
∆Ф = B∆S = Bπfl2∆t
ξi =
α
φ0 – φl = πBfl2
φ0 – φl = πBfl2 +
X
A
≈3,14 (B)
В
Металлический стержень длиной L и
массой m лежит на гладком столе и
соединен одинаковыми легкими
проводящими пружинами жёсткостью к
каждая с укрепленной на столе планкой.
Система находится в однородном
магнитном поле. После того как по
стержню пропустили кратковременный
ток, он стал совершать гармонические
колебания. За время протекания тока по
стержню прошел заряд Q, смещением
стержня за это время можно пренебречь.
1) Чему равна кинетическая энергия
стержня сразу после выключения тока?
2) Чему равна амплитуда колебаний стержня?