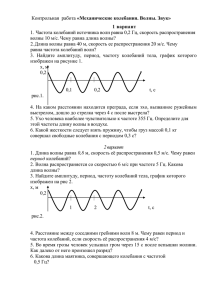
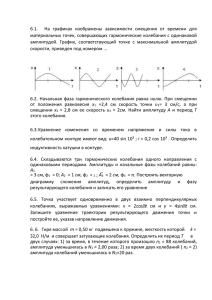
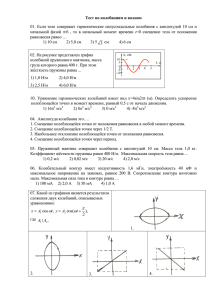
s=A cos(ῳ 0 t+ϕ)

Колебания и их
характеристики
Колебания – движения или
процессы, характеризующиеся
определенной повторяемостью во
времени.
Колебания, при которых колеблющаяся величина
изменяется по закону синуса или косинуса
Важность рассмотрения гармонических
колебаний.
 Колебания, встречающиеся в природе и технике,
близки к гармоническим.
 Различные периодические процессы
(процессы, повторяющиеся через равные
промежутки времени) можно представить как
наложение гармонических колебаний.
Гармоническое колебание величины s
описывается уравнениями типа
s=A cos(ῳ0t+ϕ) или s=A sin(ῳ0t+ϕ).
[A-амплитуда колебаний; ῳ0-круговая(циклическая)
частота; ϕ-начальная фаза колебаний; (ῳ0t+ϕ)-фаза
колебаний в момент времени t ]
Гармоническое колебание величины s.
s=A cos(ῳ0t+ϕ)
ds/dt= -A ῳ0sin (ῳ0t+ϕ)=
= A ῳ0cos (ῳ0t+ϕ+π/2)
Вторая производная по времени от
гармонически колеблющейся величины s.
2
2
d s/dt =
-A ῳ20 cos(ῳ0t+ϕ)=
= A ῳ20cos (ῳ0t+ϕ+π)
d2s/dt2 + ῳ20 s=0,
или ṥ+ ῳ20 s=0
Получается из выражения d2s/dt2,
где s=A cos(ῳ0t+ϕ)
Смещение, скорость и ускорение
колеблющейся точки.
Материальная точка совершает прямолинейные
гармонические колебания вдоль оси координат x
около положения равновесия, принятого за начало
координат.
x=A cos(ῳ0t+ϕ)
Скорость колеблющейся точки.
ѵ=dx/dt= -A ῳ0 sin(ῳ0t+ϕ)=
= A ῳ0cos (ῳ0t+ϕ+π/2)
a=dѵ/dt=-A ῳ20 cos(ῳ0t+ϕ)=
=A ῳ20cos(ῳ0t+ϕ+π)
F=ma=-m ῳ x
2
0
Пропорциональная смешению материальной точки и
направлена в противоположную сторону (к
положению равновесия).
[A-амплитуда колебания; ῳ0-циклическая частота;
(ῳ0t+ϕ)-фаза колебания;m-масса колеблющейся
точки]
Кинетическая энергия колеблющейся
материальной точки.
mA202
mv 2
T 

sin 2 (0t   ) 
2
4
 mA202 [1  cos 2(0t   )
m02 x 2 mA202
П    F dx 

cos 2 (0t   ) 
2
4
0
x
mA202

[1  cos 2(0t   )]
4
mA 
E Т  П
4
2
2
0
Т и П изменяются с
частотой 2ῳ0,т.е. с
удвоенно частотой
гармонического
колебания.
<Т>=<П>=Е/2
Поскольку
<sin2a>=<cos2a>=1/2.
Пружинный.
Груз массой m,
подвешенный на
абсолютно упругой
пружине и совершающий
гармонические колебания
под действием упругой
силы, F=-kx.
[k-жесткость пружины]
Математический.
Идеализированная
система, состоящая из
материальной точки
массой m,
подвешенной на
нерастяжимой
невесомой нити и
колеблющейся под
действием силы
тяжести.
Физический.
Твердое тело,
совершающее под
действием силы тяжести
колебания вокруг
неподвижной
горизонтальной оси,
проходящей через точку О,
не совпадающую с
центром масс С тел (точка
О- точка подвеса)
Колебательный контур.
Цепь, состоящая из включенных последовательно
катушки индуктивностью L, конденсатора
емкостью С и резистора сопротивления R.
Предназначение. Для возбуждения и поддержания
электромагнитных колебаний (периодических
процессов превращения энергии электрического
поля в энергию магнитного поля, и наоборот)
Второе правило Кирхгофа для контура
UC=ƐS
[UC=Q/C-напряжение на конденсаторе;
ƐS =-L( dI/dt) -ЭДС самоиндукции, возникающая
в катушке при протекании в ней переменного
тока]
1


Q
Q0
LC
Подставили UC и ƐS во второе правило Кирхгофа и
учли, что
dI


I Qи
Q
dt
Q=Qm cos(ῳ0t+ϕ)
Колебания свободные (отсутствуют внешние ЭДС)
и гармонические (R=0)
[Qm –амплитуда колебаний заряда на обкладках
конденсатора]
0 
1
LC
Это - циклическая частота свободных
незатухающих колебаний.
2
T  ; T  2 LC
0
Формула Томпсона

I  Q  0Qm sin( 0t   ) 

 I m cos(0t    )
2
[Im= ῳ0Qm амплитуда силы тока]
Qm
Q
UC 

cos(0t   ) 
C
C
 U m cos(0t   )
Колебания тока I опережают по фазе колебания заряда
(и колебания напряжения) на π/2, т.е., когда ток
достигает максимального значения, заряд, а также
напряжение обращаются в нуль, и наоборот.
[Um=Qm/C-амплитуда напряжения]
Свободные затухающие
колебания
линейной системы.
Свободные колебания,
амплитуда которых из-за
потерь энергии реальной
колебательной системой с
течением времени
уменьшается.
Превращение в теплоту из-за трения в
механических колебательных системах,
омические потери и излучение
электромагнитной энергии в
электрических колебательных системах.
Закон затухания определяется свойствами
колебательных систем.
Идеализированные реальные системы, в
которых параметры, определяющие
физические свойства системы, в ходе
процесса не изменяются.
Примеры линейных систем: пружинный
маятник при малых растяжениях пружины,
колебательный контур, индуктивность,
емкость и сопротивление которого не
зависят ни от тока в контуре, ни от
напряжения.
A(t )
T
e
A(t  T )
A(t) и A(t+T)-амплитуды двух последовательных
колебаний,
соответствующих моментам
времени, отличающимся на период.
 
1

Промежуток времени, в течении которого
амплитуда затухающих колебаний уменьшается
в е раз.
A(t )
T 1
  ln
 T  
A(t  T )
 Ne
[τ-время релаксации; Ne –число колебаний,
совершаемых за время уменьшения амплитуды в
е раз]
Вынужденные механические
колебания- незатухающие
колебания, возникающие под
действием внешней периодически
меняющейся силы F=F0cosωt (F0амплитудное значение вынуждающей
силы, ω-частота вынуждающей силы).
mx  kx  rx  F0 cos t
[-kx-сила упругости; –rѵ=-rẋ-сила трения; F0cosωtвынуждающая сила]
F0
k
r
x  
x
x 
cos t
m
m
m
F0
2
x  2x  0 x 
cos t
m
Учли, что собственная частота
и коэффициент затухания
0 
 
r
2m
k
m
A
F0 /m
(   )  4 
2
0
[0 
2 2
k
r
; 
]
m
2m
2
2
Частота, при которой
амплитуда смещения достигает
максимума.
d
2
2 2
2
2
[(0   )  4  ]  0
dt
2
2
2
 4(0   )  8   0
 рез 
  2
2
0
2
Продифференцировали подкоренное выражение
для А по ω и приравняли его нулю.
Арез 
F0
2m   
2
0
2
Подставили в формулу для А
резонансную частоту.
Механический резонансявление резкого возрастания
амплитуды вынужденных
колебаний при приближении
частоты вынуждающей силы к
частоте, равной или близкой
собственной частоте
колебательной системы.
Амплитудные резонансные кривыезависимости амплитуды А вынужденных
колебаний от частоты ω при различных δ (см.
рисунок). При ω→0 все кривые достигают
одного и того же, отличного от нуля,
предельного значения F0/mω20, называемого
статическим отклонением (см. рисунок). При
ω→∞ все кривые асимптотически стремятся
к нулю. Чем больше коэффициент затухания,
тем ниже и левее максимумы резонансных
кривых.
Переменный ток- электрический ток,
величина и направление которого
изменяются во времени.
Установившиеся вынужденные
электромагнитные колебания можно
рассматривать как протекание
переменного тока в цепи, содержащей
резистор, катушку индуктивности и
конденсатор.
Цепь, содержащая резистор, катушку
индуктивности и конденсатор, к которой
приложено переменное напряжение.
U=Umcosωt
[Um -амплитудное значение напряжения]
Для переменного тока мгновенные
значения силы тока во всех сечениях цепи
практически одинаковы, так как их
изменения происходят достаточно
медленно, а электромагнитные
возмущения распространяются по цепи со
скоростью, равной скорости света.
Напряжение, приложенное к концам участка цепи
(рисунок а).
U=Umcosωt
U Um
I 
cos t  I m cos t
R
R
Im
Um

R
На рисунке б векторная диаграмма
амплитудных значений силы тока Im и
напряжения Um на резисторе (сдвиг фаз между
Im и Um равен нулю)
Напряжение, приложенное к концам участка
цепи (рисунок а)
U=Umcosωt
Q
U c  U m cos t
C
dQ
I
 CU m sin t 
dt

 I m cos(t  )
2
Um
I m  CU m 
1 / C
RC=1/ωC- реактивное емкостное сопротивление
1
UC 
I m cos t
C
Падение напряжения Uc отстает по фазе от тока I
на π/2,что и показано на векторной диаграмме
(рисунок б) и на графиках.
Напряжение, приложенное к концам участка
цепи (рис. а)
U=Umcosωt
U   S ,
dI
U m cos t  L
 0,
dt
dI
L
 U m cos t (*)
dt
dI
UL  L
dt
Поскольку внешнее напряжение приложено к
катушке индуктивности.
Um
Um

I 
sin t 
cos(t  ) 
L
L
2
 I m cos(t 

2
)
После интегрирования выражения
получаемого из формулы (*).
Um
dI 
cos tdt,
L
Im
Um

L
RL=ωL-реактивное индуктивное сопротивление.
U L  LI m cos t
Падение напряжения UL опережает по фазе ток
I,текущий через катушку, на π/2,что и показано
на векторной диаграмме (рисунок б) и на
графиках.
Напряжение, приложенное к концам
участка цепи (рисунок а).
U=Umcosωt
UR+UL+UC=U
[UR,UL и UC-соответствующие падения напряжений на
сопротивлении, катушке индуктивности и
конденсаторе]
Равна векторной сумме амплитуд всех падений
напряжения в цепи (рисунок б).
1
L 

C
tg 
R
(см. рисунок б)
(*)
Im 
Um
1 2
R  (L 
)
C
2
(см. рисунок б):
1
( RI m )  [(L 
) I m ]2  U m2
C
2
I=Imcos(ωt-ϕ)
Сдвиг по фазе ϕ между током I и приложенным
напряжением определяется формулой (*).
1 2
Z  R  (L 
) 
C
2
 R  ( RL  RC )
2
2
X=RL-RC=ωL-1/ωC
[R-активное сопротивление; RL- реактивное
индуктивное сопротивление; RC-реактивное
емкостное сопротивление]
P(t)=U(t)I(t)
Определяется произведением мгновенных
значений напряжения и силы тока.
P(t)=ImUm cos(ωt-ϕ)cosωt
<P>=1/2 ImUm cosϕ
2
<P>=1/2 RI m
Так как <cos2ωt>=1/2, то <sinωt cosωt>=0
Umcosϕ=RIm (векторная диаграмма)
Такую же мощность развивает постоянный ток
= Im/√2
I
Действующее (эффективное)
значение тока:
I=Im/√2
Действующее (эффективное)
значение напряжения:
U=Um/√2
<P>=IUcosϕ
Учли действующие значения тока и
напряжения.
cos  
R
1 2
R  [L 
]
C
2
Мощность, выделяемая в цепи переменного тока,
в общем случае зависит не только от силы тока и
напряжения, но и от сдвига фаз между ними. Если в
цепи реактивное сопротивление отсутствует, то
cosϕ=1 и P=IU. Если цепь содержит только
реактивное сопротивление (R=0),то cosϕ=0 и
средняя мощность равна нулю, какими бы
большими ни были ток и напряжение.
Сплошная среда- среда, непрерывно
распределенная в пространстве и
обладающая упругими свойствами.
Волновой процесс(волна)-процесс
распространения колебаний в сплошной
среде. При распространении волны
частицы среды колеблются около своих
равновесных положений.
Основное свойство всех волн.
Вместе с волной от частицы к
частице среды передается состояние
колебательного движения и его
энергия. Поэтому основное свойство
всех волн, независимо от их
природы,- перенос энергии без
переноса вещества.
Продольные волны-волны, в которых частицы
среды колеблются в направлении
распространения волны. Продольные волны
могут распространяться в среде, где
возникают упругие силы при деформациях
сжатия и растяжения, т.е. в твердых телах,
жидкостях и газах.
Поперечные волны- волны, в которых
частицы среды колеблются в
направлениях, перпендикулярных
направлению распространению волны.
Поперечные упругие волны могут
распространяться в среде, где возникают
упругие силы при деформации сдвига, т.е.
в твердых телах.
Однородная среда- среда, физические
свойства которой не изменяются от точки
к точке среды.
Изотропная среда- среда, физические
свойства которой одинаковы во всех
направлениях.
Волновой фронт- геометрическое место точек, до
которых доходят колебания к моменту времени t.
 Форма фронта волны определяется
конфигурацией источника и свойствами среды.
Волновая поверхность- геометрическое место
точек, колеблющихся в одинаковой фазе.
 В случае однородной и изотропной среды
волновой фронт является одной из волновых
поверхностей.
Луч- линия, касательная к которой в каждой
точке совпадает с направлением
распространения волны. В случае
однородной и изотропной среды лучпрямая, перпендикулярная волновой
поверхности и совпадающая с
направлением переноса энергии волной.
Плоские волны- волны, для которых
волновые поверхности- совокупность
параллельных плоскостей,
перпендикулярных направлению
распространения волны.
Сферические волны- волны, для которых
волновые поверхности- совокупность
концентрических сфер.
Гармоническая волна.
Упругая волна называется
гармонической, если
соответствующие ей колебания
частиц среды являются
гармоническими.
Это зависимость между смещением ξ частиц
среды, участвующих в волновом процессе, и
расстоянием х этих частиц(например, частицы
В) от источника колебаний О для какого-то
фиксированного момента времени t. Рисунок
задает мгновенную картину распределения
возмущения вдоль направления
распространения, и его не следует воспринимать
как зримое изображение волны.
Эти графики различны по
существу. Если график
волны определяет
зависимость смещения всех
частиц среды от расстояния
до источника колебаний в
данный момент времени, то
график колебаниязависимость смещения
данной частицы от времени.
  T
  v
Расстояние между двумя ближайшими частицами,
колеблющимися в одинаковой фазе. Длина
волны равна расстоянию, на которое
распространяется определенная фаза колебания
за период.
2
2





T 
[ѵ- скорость волны; T- период волны; v-частота
колебаний; ω- циклическая частота волны ]
x
 ( x, t )  A cos[ (t  )   0 ]

[ξ(x,t)- смещение точек среды с координатой x в
момент времени t; A- амплитуда волны; ωциклическая (круговая) частота;ѵ- фазовая
скорость;ϕ0 –начальная фаза колебаний]

dx

dt
Скорость перемещения волны.



k
Зависимость фазовой скорости волн в среде
от их частоты.
A0
 (r , t ) 
cos(t  kr   0 )
r
В случае сферической волны даже в среде, не
поглощающей энергию, амплитуда колебаний не
остается постоянной, а убывает с расстоянием
по закону 1/r.
  
1 
 2  2  2 2
2
x
y
z
 t
2
2
2
2
1 
  2 2
 t
2
[ϑ-фазовая скорость;
  
  2  2  2 - оператор Лапласа]
x
z
y
2
2
2

1 

2
2
2
x
 t
2
2
Решение- уравнение плоской волны ξ=Acos(ωtkx+φ0 )
Линейная среда- среда, в которой при
одновременном распространении нескольких
волн ее свойства не изменяются под действием
возмущений, создаваемых волной.
Принцип суперпозиции (наложения)
волн.
При распространении в линейной среде нескольких
волн каждая из них распространяется так, как будто
другие волны отсутствуют, а результирующее
смещение частицы среды в любой момент времени
равно геометрической сумме смещений, которые
получают частицы среды, участвуя в каждом из
независимых волновых процессов. Например, если
волны распространяются от двух источников, то
они, доходя до какой-то точки, вызывают ее
колебания независимо друг от друга.
Когерентность- согласованное протекание во
времени и пространстве нескольких колебательных
или волновых процессов.
Когерентные волны- волны, разность фаз
которых остается постоянной во времени.
Когерентными могут быть лишь волны, имеющие
одинаковую частоту.
Интерференция волн- явление наложения
двух (или нескольких) когерентных волн, при
котором в разных точках пространства
получается усиление или ослабление
результирующей волны в зависимости от
соотношения между фазами этих волн.
∆=r1–r2
Поскольку для когерентных источников разность
начальных фаз φ1-φ2=const,результат наложения
двух волн в различных точках зависит от разности
хода.
k (r1  r2 )  ( 1   2 )  2m
(m  0, 1, 2,...)
Амплитуда результирующего колебания
A0 A0
A

r1
r2
k (r1  r2 )  (1   2 )  (2m  1)
(m  0, 1, 2,...)
Амплитуда результирующего колебания
A0 A0
A

r1 r2
Акустика- область физики, в которой изучаются
звуковые волны.
Звуковые (акустические) волны- упругие
волны с частотами 16-20000Гц,
распространяющиеся в среде и воспринимаемые
органами слуха человека (границы условны, т.е.
для разных людей они различны)
Инфразвуковые волны- звуковые волны
с
частотами ниже границ диапазона восприятия
уха человека, т.е. ν<16Гц.
Ультразвуковые волны- звуковые волны с
частотами выше диапазона слуха человека, т.е.
ν>20кГц.
В жидкостях и газах они могут быть только
продольными, так как эти среды обладают
упругостью лишь по отношению к деформациям
сжатия (растяжения). В твердых телах могут
быть как продольными, так и поперечными, так
как твердые тела обладают упругостью по
отношению к деформациям сжатия (растяжения)
и сдвига.
Интенсивность (или сила) звукаэнергетическая характеристика: величина,
определяемая средней по времени энергией,
переносимой звуковой волной в единицу
времени сквозь площадку, ориентированную
перпендикулярно направлению
распространению волны.
Чувствительность человеческого уха различна
для разных частот. Для каждой частоты
колебаний существует наименьшая (порог
слышимости) и наибольшая (порог болевого
ощущения) интенсивности звука, которые
способны вызвать звуковое восприятие.
Громкость звука- субъективная
характеристика: величина, характеризующая
слуховое ощущение для данного звука и зависящая
от интенсивности звука, частоты и формы звуковых
колебаний.
Уровень интенсивности звука- объективная
оценка громкости звука: L=lg I/I0
I0 –интенсивность звука на пороге слышимости,
принимаемая для всех звуков равной 10-12 Вт/м2.
Величина L выражается в белах (Б),а чаще- в
единицах, в десять раз меньших,- децибелах (дБ).
Уровень громкости- физиологическая
характеристика: выражается в фонах. Громкость
для звука 1000Гц равна 1 фон, если его уровень
интенсивности равен 1 дБ.
Высота звука- субъективная характеристика:
качество периодического или почти периодического
звука, определяемое человеком на слух и зависящее
от частоты звука. С ростом частоты звука
увеличивается (звук становится «выше»),с
уменьшением частоты- понижается.
Реальный звук- наложение гармонических
колебаний с большим набором частот.
Акустический спектр:


сплошной -в некотором интервале присутствуют
колебания всех частот.
линейчатый -присутствуют отдельные друг от
друга определенные частоты.
Музыкальные звуки- звуки, обладающие
линейчатым спектром (например, звуки
музыкальных инструментов). Ряд нот- ряд звуков с
возрастающей высотой тона с регулярными
интервалами.
Шумы-звуки, обладающие сплошным спектром
или линейчатым спектром с негармоническими
составляющими.
Эффект Доплера заключается в том,
что испускаемая и регистрируемая
частота волны различаются, если
источник и приемник движутся друг
относительно друга в среде, где
распространяется среда.
Электромагнитные волны.
Переменное электромагнитное поле,
распространяющееся в пространстве с конечной
скоростью.
Электромагнитные волны возникают в
результате того, что переменное электрическое
поле порождает переменное магнитное поле,
которое порождает переменное электрическое
поле.
Источники электромагнитных
волн.
Источником электромагнитных волн может быть
любой колебательный контур или проводник, по
которому течет переменный электрический ток, так
как для возбуждения электромагнитных волн
необходимо создать в пространстве переменное
электрическое поле или соответственно переменное
магнитное поле.
Для получения электромагнитных
волн непригодны закрытые
колебательные контуры, так как в них
электрическое поле сосредоточено
между обкладками конденсатора, а
магнитное- внутри катушки
индуктивности.
1
1
c


 0 0 

[ε0 и μ0 –электрическая и магнитная постоянные; ε
и μ- диэлектрическая и магнитная
проницаемости среды; с-скорость
распространения света в вакууме]
c
1
 0 0
Совпадение размерного коэффициента в формуле
для фазовой скорости со скоростью с указывает
на глубокую связь между электромагнитными и
оптическими явлениями.
Эти уравнения-следствия уравнений
Максвелла. Они отвечают однородной и
изотропной среде вдали от заряда и токов,
создающих электромагнитное поле.
Всякая функция, удовлетворяющая
записанным уравнениям, описывает некоторую
волну, т.е. электромагнитные поля действительно
могут существовать в виде электромагнитных
волн.

 1 2E
E  2 2 ,
 t

2

1  H
H  2
2
 t
[
  
 2  2  2
x z y
2
2
2
- оператор Лапласа;ν-фазовая
скорость]
 Ey
1  Ey
 2
,
2
2
x
 t
2H z
1 2H z
 2
2
2
x
 t
2
2
Эти уравнения удовлетворяют плоские
монохроматические волны, описываемые
уравнениями:
Ey=E0ycos (ωt-kx+φ)
Hz=H0zcos (ωt-kx+φ)