Основные уравнения
реклама

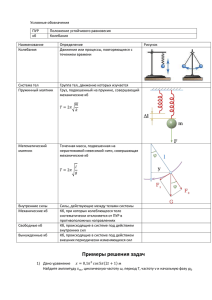
Основные уравнения механических колебательных движений Везде, где есть соображение, есть разум; везде, где есть разум, есть торжество. Буаст k x m уравнение координаты, описывающее колебания пружинного маятника x’’= – g x l уравнение координаты, описывающее колебания математического маятника x’’= – m T 2 k период колебаний пружинного маятника m 2 2 кинетическая энергия колеблющейся точки kA2 2 потенциальная энергия колеблющейся точки Ek Ep решения уравнений x A cos t , координаты x’= m sin t , скорости Аналогия между механическими параметрами и электрическими arctg x–q –I 2 m–L 1 С 2 kx q2 – 2 2C 2 m LI 2 – 2 2 k– полное сопротивление в цепи переменного тока F Fm sin t , силы L 1 C R сдвиг по фазе между электрическим напряжением и силой тока x’’– q’’ 2 2 1 Z R L C x’’= a a m cos t , ускорения 1 q LC основное уравнение свободных электромагнитных колебаний q’’= – a – I’ l T 2 g период колебаний математического маятника Основные уравнения электромагнитных колебательных движений T 2 LC формула Томсона, период колебаний колебательного контура Wм= Wmм LI m2 2 энергия магнитного поля катушки индуктивности Wэ= Wmэ энергия электрическог о поля конденсатора решения уравнений q=qmcos t 0 , колебания заряда U U m cost 0 , напряжения q’= i I m cost 0 , силы тока m cost 0 , колебания ЭДС 2 , связь циклической частоты, периода, частоты T 1 1 , частота через период, T , период через частоту T t 0 , фаза колебаний, 1 2 , разность фаз U Um 2 , I Im 2 q m2 2C , действующее значение напряжения и силы тока E E0 sin t B B0 sin t Переменный ток – ток, периодически меняющийся по величине и направлению, незатухающие вынужденные электромагнитные колебания