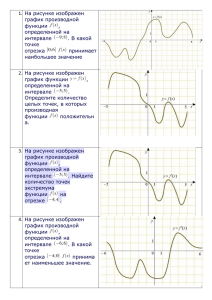
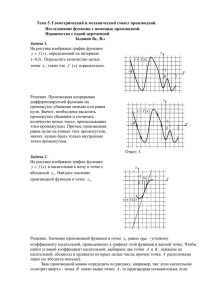
Чтение графика функции или графика производной функции
реклама

Элементы математического анализа в ЕГЭ Малиновская Галина Михайловна malinogalina@yandex.ru Справочный материал Таблица производных основных функций. Правила дифференцирования (производная суммы, произведения, частного двух функций). Производная сложной функции. Геометрический смысл производной. Физический смысл производной. Справочный материал Точки экстремума (максимума или минимума) функции, заданной графически. Нахождение наибольшего (наименьшего) значения функции, непрерывной на заданном отрезке. Первообразная функции. Формула Ньютона-Лейбница. Нахождение площади криволинейной трапеции. Физические приложения 1.1 Материальная точка движется прямолинейно по закону 𝑥 𝑡 = −𝑡 4 +6𝑡 3 +5𝑡 + 23 , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t= 3с. 1.2 Материальная точка движется 1 3 прямолинейно по закону 𝑥 𝑡 = 𝑡 − 3 3𝑡 2 − 5𝑡 + 3 , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с? Решение: Ищем производную х(t) (функции пути по времени). В задаче 1.1 подставляем вместо t его значение и считаем скорость (Ответ: 59). Во задаче 1.2 приравниваем найденную производную к данному числу и решаем уравнение относительно переменной t. (Ответ: 7). Геометрические приложения 2.1 Прямая 𝑦 = 7𝑥 − 5 параллельна касательной к графику 2 функции 𝑦 = 𝑥 + 6𝑥 − 8 . Найдите абсциссу точки касания. 2.2 Прямая 𝑦 = 3𝑥 + 1 является касательной к 2 графику функции 𝑎𝑥 + 2𝑥 + 3 . Найдите a. 2.3 Прямая 𝑦 = −5𝑥 + 8 является касательной к 2 графику функции 28𝑥 + 𝑏𝑥 + 15 . Найдите b, учитывая, что абсцисса точки касания больше 0. 2.4 Прямая 𝑦 = 3𝑥 + 4 является касательной к графику 2 функции 3𝑥 − 3𝑥 + 𝑐. Найдите c. Решение: В задаче 2.1 ищем производную функции и приравниваем к угловому коэффициенту прямой (Ответ: 0,5). В задачах 2.2-2.4 составляем систему из двух уравнений. В одном приравниваем функции, в другом приравниваем их производные. В системе с двумя неизвестными (переменной x и параметра) ищем параметр. (Ответы: 2.2) a=0,125; 2.3) b=-33; 2.4) c=7). 2.5 На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой 𝑥0 . Найдите значение производной функции f(x) в точке 𝑥0 . 2.6 На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой 𝑥0 . Найдите значение производной функции f(x) в точке 𝑥0 . 2.7 На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке .x=10. 𝑥0 = 0 Решение: Значение производной функции в точке - это тангенс угла наклона касательной к графику функции, проведенной в данной точке. «Дорисовываем» прямоугольный треугольник и ищем тангенс соответствующего угла, который берем положительным, если касательная образует острый угол с положительным направлением оси Ох (касательная «растёт») и отрицательным, если угол тупой (касательная убывает). В задаче 2.7 необходимо провести касательную через указанную точку и начало координат. Ответы: 2.5) 0,25; 2.6) -0,25; 2.7) -0,6. Чтение графика функции или графика производной функции 3.1 На рисунке изображен график функции y=f(x), определенной на интервале (6;8). Определите количество целых точек, в которых производная функции положительна. 3.2 На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна. Решение: Знак производной связан с поведением функции. Если производная положительна, то выделяем ту часть графика функции, где функция возрастает. Если производная отрицательна то там, где функция убывает. Выделяем соответствующий этой части промежуток на оси Ох. В соответствии с вопросом задачи или пересчитываем количество целых чисел, входящих в данный промежуток или находим их сумму. Ответы: 3.1) 4; 3.2) 8. 3.3 На рисунке изображен график функции y=f(x), определенной на интервале (-2;12). Найдите сумму точек экстремума функции f(x). В первую очередь смотрим, что на рисунке: график функции или график производной. Если это график производной, то нас интересуют только знаки производной и абсциссы точек пересечения с осью Ох. Для наглядности можно нарисовать более привычный рисунок со знаками производной по полученным промежуткам и поведением функции. В соответствии с рисунком ответить на вопрос задачи. (Ответ: 3.3) 44). 3.4 На рисунке изображен график ′ y=𝑓 (𝑥) — производной функции f(x), определенной на интервале (-7;14]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9]. 3.5 На рисунке изображен график y=𝑓 ′ (𝑥) — производной функции f(x), определенной на интервале (-11;11) . Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10]. Решение: Ищем точки пересечения графика производной с осью Ох, выделяя ту часть оси, которая указана в задаче. Определяем знак производной на каждом из полученных промежутков (если график производной ниже оси-то «-», если выше-то «+»). Точками максимума будут те, где знак сменился с «+» на «-», минимума- с «-» на «+». Точками экстремума те и другие. Ответы: 3.4) 1; 3.5) 5. 3.6 На рисунке изображен график y=𝑓 ′ (𝑥) — производной функции f(x), определенной на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение. 3.7 На рисунке изображен график ′ y=𝑓 (𝑥) — производной функции f(x), определенной на интервале (-8;4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение. Решение: Если производная меняет знак на рассматриваемом отрезке, то решение основано на теореме: если непрерывная на отрезке функция имеет на нем единственную точку экстремума и это точка максимума (минимума), то наибольшее (наименьшее) значение функции на этом отрезке достигается в данной точке. Если непрерывная на отрезке функция монотонна, то она достигает своих наименьшего и наибольшего значений на данном отрезке на его концах. Ответы: 3.6) -3; 3.7) -7. 3.8 На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней. 3.9 На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: 𝑥1 ,𝑥2 ,𝑥3 , … , 𝑥12 . В скольких из этих точек производная функции f(x) положительна? 4.2 На рисунке изображен график y=𝑓 ′ (𝑥) — производной функции f(x), определенной на интервале (-5;7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки. 4.5 На рисунке изображен график y=𝑓 ′ (𝑥)— производной функции f(x), определенной на интервале (-4;8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2;6]. 4.6 На рисунке изображен график y=𝑓 ′ (𝑥)— производной функции f(x), определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=-2x-11 или совпадает с ней. Решение: 4.6 Так как на рисунке изображен график производной, а касательная параллельна данной прямой, то производная функции в этой точке равна -2. Ищем точки на графике производной с ординатой равной -2 и считаем их количество. Получаем 5. Ответы: 3.8) 4; 3.9) 5; 4.2) 18; 4.5) 4; 4.6) 5. 4.8 На рисунке изображен график y=𝑓 ′ (𝑥)— производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней. Решение: Если прямая параллельна оси Ох, то её угловой коэффициент равен нулю. Угловой коэффициент касательной равен нулю, значит производная равна нулю. Ищем абсциссу точки пересечения графика производной с осью Ох. Получаем -3. 4.9 На рисунке изображён график функции y=𝑓 ′ (x) производная функции f(x) и восемь точек на оси абсцисс: 𝑥1 ,𝑥2 ,𝑥3 , … , 𝑥8 . В скольких из этих точек производная функции f(x) возрастает? Геометрический смысл определенного интеграла 5.1 На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8)-F(2), где F(x) — одна из первообразных функции f(x). Решение: Площадь криволинейной трапеции вычисляется через определённый интеграл. Определённый интеграл вычисляется по формуле Ньютона-Лейбница как приращение первообразной. В задаче 5.1 считаем площадь трапеции по известной формуле курса геометрии (это и будет приращение первообразной). В задачах 5.2 и 5.3 уже дана первообразная. Необходимо вычислить её значения на концах отрезка и посчитать разность. 5.2 На рисунке изображён график некоторой функции y=f(x). Функция 𝐹 𝑥 = 15 3 2 𝑥 + 30𝑥 + 302𝑥 − — одна из 8 первообразных функции f(x). Найдите площадь закрашенной фигуры. Решение: Площадь криволинейной трапеции вычисляется через определённый интеграл. Определённый интеграл вычисляется по формуле Ньютона-Лейбница как приращение первообразной. В задаче 5.1 считаем площадь трапеции по известной формуле курса геометрии (это и будет приращение первообразной). В задаче 5.2 уже дана первообразная. Необходимо вычислить её значения на концах отрезка и посчитать разность. Удачи на ЕГЭ по математике