РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ С ИСПОЛЬЗОВАНИЕМ ЭОР «ЖИВАЯ ФИЗИКА» «
реклама

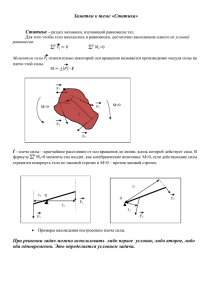
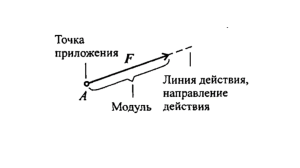
РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ С ИСПОЛЬЗОВАНИЕМ ЭОР «ЖИВАЯ ФИЗИКА» «Мы занимаемся творчеством всякий раз, когда выражаем сложную мысль или заполняем текстом чистый лист бумаги. Если мы делаем это эффективно и необычно – значит, нас по праву можно назвать творческими людьми.» Джеймс Алан Гарднер Выполнили: Семененко Н.М., Жевлакова Е.В., Новикова О.А. Руководитель: Заседатель В.С., старший преподаватель,ФФ ТГУ Главная задача современной школы: раскрытие коммуникативных способностей каждого обучающегося, воспитание личности, готовой к жизни в высокотехнологичном мире. Средством достижения этой цели является использование для организации учебно-воспитательного процесса информационно-коммуникационных технологий. Физика – один из тех учебных предметов, при обучении которому ИКТ могут быть применены в различных вариантах. Для решения задач, кроме знания тем курса физики, заключающегося в знании и понимании физических законов, которым подчиняются описываемые в условии задачи явления, и владения математическим аппаратом, требуется от обучающихся способность понимать условие и представлять физическую ситуацию, соответствующую условию задачи. Одним из методических приемов в решении задач служит применение интерактивных учебных программ, позволяющих продемонстрировать школьнику разные уровни моделирования физических явлений, что приводит к правильному пониманию условия задачи и успешному ее решению. Компьютерная проектная среда «Живая физика» предоставляет возможности для интерактивного моделирования движения в гравитационном, электростатическом магнитном или любых других полях, а также движения, вызванного всевозможными видами взаимодействия объектов. В качестве примера рассмотрены случаи моделирования следующих кинематических ситуаций: Задача В устройстве, изображенном на рис.1, все блоки невесомы, а их оси хорошо смазаны. Легкая нерастяжимая нить, переброшенная через блоки, связывает станину массой M с грузом массой m. Между грузом и станиной трение пренебрежимо мало. Груз, опускаясь под действием силы тяжести, подтягивает станину к вертикальной стене. Найти ускорение станины и ускорение груза. Трения между станиной и плоскостью нет. Порядок выполнения работы: Войти в программу «Живая Физика»; В разделе «Среда» установить тип поля (в нашем случае – гравитация) и его параметры. Выбрать в соответствии с условием задачи для виртуальной модели объекты и разместить их на рабочем поле. Это станина 1, груз 2, блоки 3. Определить свойства объектов (задать массы станины и груза, для коэффициентов трения выбрать нулевые значения). В разделе «Измерения» выбрать ускорения, силы, при необходимости другие физические величины, которые будут отображаться в виде графической информации. В разделе «Окно-изображение» выбрать удобный дизайн интерфейса. Запуск программы осуществляется кнопкой «Старт». 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 13:04:31 6/19/2015 Пластина 30: ускорение по X t Ax 0.000 0.708 0.125 0.743 0.250 0.757 0.375 0.660 0.500 0.747 0.625 0.745 0.750 0.734 0.875 0.727 1.000 0.724 1.125 0.724 1.250 0.725 1.375 0.727 1.500 0.727 1.625 0.727 1.750 0.727 1.875 0.727 2.000 0.727 2.125 0.727 2.250 0.727 Кубик 10: ускорение по Y t Ay 0.000 -2.043 0.12 -1.625 0.25 -1.408 0.37 -1.223 0.500 -1.409 0.625 -1.428 0.750 -1.435 0.875 -1.442 1.000 -1.446 1.125 -1.449 1.250 -1.451 1.375 -1.455 1.500 -1.454 1.62 -1.454 1.75 -1.454 1.875 -1.454 2.00 -1.453 2.125 -1.453 2.250 -1.453 ЭТАП РЕШЕНИЯ ТЕОРЕТИЧЕСКОЙ ЗАДАЧИ Расставим силы, действующие на станину и на груз (рис.5). Уравнения движения этих тел с учетом невесомости нити (T1=T2=T) в векторном виде имеют вид: (m+M) аст = 2Т, (1) 𝑚гр 𝑎гр =mg +Т. (2) Запишем уравнения (1) и (2) в проекциях на оси координат: (3) Получили два уравнения с тремя неизвестными. Взаимосвязь между ускорениями груза вдоль оси ординат и станины получим из условия нерастяжимости нити. Длина нити складывается из участков: l-y+l+x+l+x= const. Дважды дифференцируя это выражение, получим 2аст =агр (5) Решая полученную систему (3-4) с учетом (5), получим аст =2mg/(5m+M), (6) агр =4mg/(5m+M). (7) Относительно Земли ускорение груза будет равно a=√(а2ст +а2гр )=√5 *2mg/(5m+M). Сопоставим полученное теоретическое решение с данными виртуального эксперимента. На рис.6 приведены данные свойств объектов (груза и станины) Из данных рис.6 находим 𝑚гр =0,5 кг, M=11 кг. Подставляя в (6) и (7), получим Что совпадает с данными виртуального эксперимента, представленными на рис.3, а это означает и правильность решения, и удачную виртуальную модель ситуации, описанной в задаче. Рассматриваемая задача соответствует высокому уровню сложности. Для облегчения ее решения и была первоначально создана виртуальная модель задачи в «Живой Физике». И эта модель подсказала подходы в теоретическом решении задачи. Разумеется, можно поступать и наоборот: решить теоретически, а затем сопоставить решение с данными виртуального эксперимента. Задача Вывести уравнение траектории конца падающего стержня, второй конец которого опирается на гладкую горизонтальную поверхность. Длина стержня l. В исходном состоянии стержень в покое и удерживается с помощью нити. Затем нить перерезают, и стержень начинает падать. Выберем систему координат, связанную с центром тяжести стержня. Пусть x и y – координаты верхнего конца стержня. Угол, который составляет стержень с горизонтальной поверхностью, равен α. Решим задачу аналитически Согласно условию скорость и координаты точки C центра масс стержня в начальный момент (t = 0) равны нулям: Vc = 0, xc = 0. На падающий стержень действует две силы (сила трения равна нулю).Вдоль оси абсцисс второй закон Ньютона запишется mac = 0, а это значит, что vc = const(t) = 0 и xc = const(t) = 0 в соответствии с начальными условиями. Центр масс (точка С) в любой момент времени расположен на оси ординат. Поэтому, в любой момент времени координаты конца стержня равны: x = ½l cos a (1) y = l sin a , (2) где a – угол, который составляет стержень с горизонтальной плоскостью. Из формул (1) x = ½l cos a (1) и (2) получим y = l sin a , (2) где a – угол, который составляет стержень с горизонтальной плоскостью. Из формул (1) и (2) получим (3) Выражение (3) описывает эллипс, значит, траекторией конца падающего стержня является эллипс с полуосями 0,5l и l. ВЫВОДЫ: При более подробном знакомстве с этим удивительным конструктором вы найдёте в нём отличный учебник по созданию различных моделей и отличную справочную базу данных, причём всё это на русском языке и официально бесплатно. Мы можем с уверенностью сказать, что «Живая Физика» является одним из лучших физических конструкторов на сегодняшний день. В газете «Физика» уже были публикации, связанные с «Живой Физикой». Желающие могут с ними познакомиться в № 4/2004 и 9/2004. Существует банк моделей, созданных учителями физики на базе «Живой Физики», – например, на сайте www.physicscomputer.by.ru. Программа «Живая Физика» позволяет усваивать основные физические концепции и сделать более наглядными абстрактные идеи и теоретические построения. При использовании данной программы графически моделируется движение систем тел, это позволяет представить перемещения ее элементов и воспользоваться принципом виртуальных перемещений. Недостатки: ограниченность количества моделей и возможностей их модернизации, невозможность построения новых моделей; относительно низкая скорость расчета; отсутствие трехмерной графики; отсутствие поддержки такой важной формы работы учащихся как решение задач.