Эконометрика_3

Модели адаптивного
прогнозирования
Экспоненциальное
сглаживание
• Экспоненциальное сглаживание очень
популярный метод прогнозирования очень
многих временных рядов.
Простое экспоненциальное
сглаживание
• Простая и прагматически ясная модель
временного ряда имеет следующий вид:
xt=b+εt
где b – константа, εt – случайная ошибка.
• Константа b относительно стабильна на
каждом временном интервале, но может
также медленно изменяться со временем.
Один из интуитивно ясных способов
выделения b состоит в том, чтобы
использовать сглаживание скользящим
средним, в котором последним наблюдениям
приписываются большие веса, чем
предпоследним, предпоследним большие
веса, чем пред-предпоследним и т.д.
• Простое экспоненциальное сглаживание
именно так и устроено.
• Здесь более старым наблюдениям
приписываются экспоненциально
убывающие веса, при этом, в отличие от
скользящего среднего, учитываются все
предшествующие наблюдения ряда, а не те,
что попали в определенное окно.
• Точная формула простого экспоненциального
сглаживания имеет вид:
• Когда эта формула применяется рекурсивно,
то каждое новое сглаженное значение
(которое является также прогнозом)
вычисляется как взвешенное среднее
текущего наблюдения и сглаженного ряда.
Очевидно, результат сглаживания зависит от
параметра α.
• Если α = 1, то предыдущие наблюдения
полностью игнорируются.
• Если α = 0, то игнорируются текущие
наблюдения.
• Значения α между 0, 1 дают промежуточные
результаты.
• Эмпирические исследования показали, что
весьма часто простое экспоненциальное
сглаживание дает достаточно точный прогноз.
• Обсудим различные теоретические и
эмпирические аргументы в пользу выбора
определенного параметра сглаживания.
Очевидно, из формулы, приведенной выше,
следует, что α должно попадать в интервал
между 0 (нулем) и 1.
• На практике обычно рекомендуется брать α
меньше 0,3.
• Однако α больше 0,3 часто дает лучший
прогноз.
• Вывод: лучше оценивать оптимально α по
данным, чем просто гадать или использовать
искусственные рекомендации.
• На практике параметр сглаживания часто
ищется с поиском на сетке.
• Возможные значения параметра разбиваются
сеткой с определенным шагом.
• Например, рассматривается сетка значений от
α = 0,1 до α = 0,9, с шагом 0,1.
• Затем выбирается α, для которого сумма
квадратов (или средних квадратов) остатков
(наблюдаемые значения минус прогнозы на
шаг вперед) является минимальной.
• Выявление и анализ тенденции временного
ряда часто производится с помощью его
выравнивания или сглаживания.
Экспоненциальное сглаживание — один из
простейших и распространенных приемов
выравнивания ряда.
• Экспоненциальное сглаживание можно
представить как фильтр, на вход которого
последовательно поступают члены исходного
ряда, а на выходе формируются текущие
значения экспоненциальной средней
• Пусть X={x1, x2,…,xT } - временной ряд.
• Экспоненциальное сглаживание ряда
осуществляется по рекуррентной формуле:
St=αxt+(1 – α)St-1
• Чем меньше α, тем в большей степени
фильтруются, подавляются колебания
исходного ряда и шума.
• Если последовательно использовать это
рекуррентное соотношение, то
экспоненциальную среднюю St можно
выразить через значения временного ряда X.
• Если к моменту начала сглаживания
существуют более ранние данные, то в
качестве начального значения S0 можно
использовать арифметическую среднюю
всех имеющихся данных или какой-то их
части.
• После появления работ Р. Брауна
экспоненциальное сглаживание часто
используется для решения задачи
краткосрочного прогнозирования
временных рядов.
• Пусть задан временной ряд:
y1, y2,…,yt
Необходимо решить задачу прогнозирования
временного ряда, т.е. найти
где D- горизонт прогнозирования.
• Такую, чтобы выполнялось соотношение
• Для того, чтобы учитывать устаревание
данных, введем невозрастающую
последовательность весов
w0, w1,…,wT, wi≥0
• Временной ряд — это множество наблюдений,
получаемых последовательно во времени.
Если время изменяется дискретно, временной
ряд называется дискретным. Мы будем
рассматривать только дискретные временные
ряды, в которых наблюдения делаются через
фиксированный интервал времени,
принимаемый за единицу счета.
• Переход от момента одного наблюдения к
моменту следующего наблюдения будем
называть шагом.
• Обозначим член временного ряда,
наблюденный в момент t, через xt.
Компоненты временного ряда ξt и εt
ненаблюдаемы. Они являются теоретическими
величинами. Их выделение и составляет предмет
анализа временного ряда в задаче
прогнозирования. Оценку будущих членов ряда
обычно делают по прогнозной модели.
Прогнозная модель —- это модель,
аппроксимирующая тренд. Прогнозы — это оценки будущих уровней ряда, а последовательность
прогнозов для различных периодов упреждения
τ = 1, 2, .... k составляет оценку тренда.
При построении прогнозной модели выдвигается
гипотеза о динамике величины ξt, т.е. о характере
тренда. Однако в связи с тем, что уверенность в
гипотезе всегда относительна, рассматриваемые
нами модели наделяются адаптивными
свойствами, способностью к корректировке
исходной гипотезы или даже к замене ее другой,
более адекватно (с точки зрения точности
прогнозов) отражающей поведение, реального
ряда. Простейшая адаптивная модель
основывается на вычислении так называемой
экспоненциальной средней.
После появления работ Р. Брауна
экспоненциальная средняя часто используется
для краткосрочного прогнозирования. В этом
случае предполагается, что ряд генерируется
моделью
xt = a1,t + εt
где a1,t — варьирующий во времени средний
уровень ряда; εt — случайные отклонения.
• Прогнозная модель имеет вид
где хτ(t) — прогноз, сделанный в момент t на τ
единиц времени (шагов) вперед; a1,t — оценка
прогнозируемой величины.
Средством оценки единственного параметра
модели служит экспоненциальная средняя
Таким образом, все свойства экспоненциальной
средней распространяются на прогнозную
модель.
В частности, если St-1 рассматривать как прогноз
на 1 шаг вперед, то в выражении
величина (xt — St-1 ) есть погрешность этого
прогноза, а новый прогноз St получается в
результате корректировки предыдущего прогноза
с учетом его ошибки. В этом и состоит существо
адаптации.
• При краткосрочном прогнозировании
желательно как можно быстрее отразить
изменения a1,t и в то же время как можно
лучше “очистить” ряд от случайных
колебаний.
Таким образом, с одной стороны, следует увеличивать вес
более свежих наблюдений, что может быть достигнуто
повышением α, с другой стороны, для сглаживания
случайных отклонений величину α нужно уменьшить. Как
видим, эти два требования находятся в противоречии.
Поиск компромиссного значения α составляет задачу
оптимизации модели.
Для уяснения процедуры расчета экспоненциальной
средней и ее свойств рассмотрим числовой пример
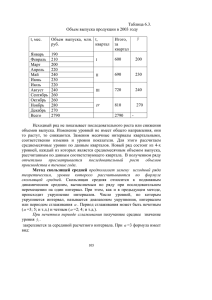
сглаживания ряда курса акций фирмы (см. табл. 1.1).
Определим S0 как
𝑆0 =
1
5
𝑥
=
𝑖=1 𝑖 5
510 + 497 + 504 + 510 + 509 = 506
Дальнейшие вычисления при α = 0,1 выглядят
следующим образом:
Результаты вычислений при α=0,1, α=0,5, α=0,9
приведены в таблице.
На рисунке приведен график динамики
временного ряда и экспоненциальных
средних при α=0,1, α=0,5. На графике
наглядно показано влияние параметра α на
подвижность экспоненциальной средней.
• Экспоненциальное сглаживание является
простейшим вариантом самообучающейся
модели. Вычисления просты и выполняются
итеративно. Они требуют даже меньше
арифметических операций, чем скользящая
средняя, а массив прошлой информации
уменьшен до одного значения St-1. Такую
модель будем называть адаптивной экспоненциального типа, а величину α —
параметром адаптации.
НАЧАЛЬНЫЕ УСЛОВИЯ
ЭКСПОНЕНЦИАЛЬНОГО
СГЛАЖИВАНИЯ
• Экспоненциальное выравнивание всегда
требует предыдущего значения
экспоненциальной средней. Когда процесс
только начинается, должна быть некоторая
величина S0, которая может быть использована
в качестве значения, предшествующего S1.
• Если есть прошлые данные к моменту
начала выравнивания, то в качестве
начального значения S0 можно
использовать арифметическую среднюю
всех имеющихся точек или какой-то их
части. Когда для такого оценивания S0 нет
данных, требуется предсказание
начального уровня ряда.
Предсказание может быть сделано исходя из
априорных знаний о процессе или на основе его
аналогии с другими процессами. После k шагов
вес, придаваемый начальному значению, равен
(1 — α)k.
Если есть уверенность в справедливости
начального значения S0, то можно коэффициент α
взять малым.
• Если такой уверенности нет, то параметру α
следует дать большое значение, с таким
расчетом, чтобы влияние начального значения
быстро уменьшилось.
• Однако большое значение α, может явиться
причиной большой дисперсии колебаний St.
• Если требуется подавление этих колебаний, то
после достаточного удаления от начального
момента времени величину α можно убавить.
• Рассмотрим роль параметра α в начальный
период сглаживания в случае, когда нет
уверенности в справедливости выбора
начальной величины S0.
• Как видно из таблицы, приведенной на
следующем слайде, составленной для значения
α = 0,1 начальная величина S0 в течение
длительного времени имеет чрезмерный вес,
Даже после 20 итераций вес S0 равен 0,122, что
означает, что ему дается все еще больший вес,
чем любому другому члену ряда. Таким
образом, в этом случае получение прогнозов по
экспоненциальной средней, построенной на
малом отрезке ряда (выборке), чревато
большими ошибками. Для того чтобы
элиминировать приданный начальной
величине.
Р. Вейд предложил следующую модификацию
метода экспоненциального сглаживания
Для исходного момента времени запишем:
где S0 – начальная оценка уровня ряда.
Так как теперь
α + α(1 – α)≠1,
то следует использовать данное выражение в
качестве множителя.
• Таким образом для момента времени t=1
получаем
Или для произвольного момента времени t
• Из анализа таблицы, приведенной на
следующем слайде, можно сделать вывод о
том, что сущность рассматриваемой
модификации Вейда заключается в том, чтобы
убрать избыточный вес начального значения S0
и распределить его пропорционально по всем
членам ряда.
• В этом случае получаемые прогнозы
основываются в большей степени на
фактических данных, а не на предварительной
оценке S0.
В целях сокращения трудоемкости вычислений
на определенном шаге необходимо будет
вернуться к обычной процедуре
экспоненциального сглаживания. Это возможно
в том случае, когда величина
приблизится к 1.
На основе эмпирического анализа Вейд
рекомендовал осуществлять такой переход при
сумме коэффициентов равной 0,995.
• При заданном значении α можно заранее
определить на каком шаге возможна
подобная трансформация.
Выбор постоянной сглаживания
Опыт показывает, что наибольшая точность
прогнозирования может быть достигнута при
любых допустимых значениях α.
Однако, как правило, если в результате
испытаний обнаружено, что наилучшее значение
константы α близко к 1, следует проверить
законность выбора модели данного типа.
• Часто к большим значениям α приводит
наличие в исследуемом ряде ярко выраженных
тенденций или сезонных колебаний.
• В этом случае для получения эффективных
прогнозов требуется другая модель.
• Наилучшее значение α в общем случае должно
зависеть от срока прогнозирования х. Для
конъюнктурных прогнозов в большей мере
должна учитываться свежая информация. При
увеличении периода упреждения х более
поздняя информация, отражающая последнюю
конъюнктуру, должна, по-видимому, иметь
несколько меньший вес, чем в случае малых х.
Для того чтобы сгладить конъюнктурные
колебания, следует в большей мере учитывать
информацию за прошлые периоды времени.
• Для проведения подобного анализа вводят
понятие среднего возраста данных. Возраст
текущего наблюдения равен 0, возраст
предыдущего наблюдения равен 1 и т. д.
Средний возраст — это сумма взвешенных
возрастов данных, использованных для подсчета сглаженной величины. Причем возраст
имеют те же веса, что и соответствующая
информация.
• При экспоненциальном выравнивании вес,
даваемый точке с возрастом k равен αβk, где
β=1 — α и средний возраст информации равен:
• Таким образом, чем меньше α, тем больше
средний возраст информации. Для
конъюнктурных прогнозов значение α надо
брать большим, а для более долгосрочных –
малым.
Теоретический анализ проблемы выбора
постоянной сглаживания при применении
простейшей модели экспоненциального
сглаживания для прогнозирования
стационарного процесса при прогнозировании
на 1 шаг вперед, показал, что оптимальное
значение параметра сглаживания в этом случае
будет определяться соотношением
где ρ1 – коэффициент авторкорреляции при
лаге 1.
Модель Хольта
Эмпирический анализ модели простого
экспоненциального сглаживания позволяет
сделать вывод о том, что с ее помощью нельзя
осуществлять прогноз для данных, имеющих ярко
выраженную тенденцию, то есть тренд.
Модель Хольта предполагает модификацию
алгоритма для случая линейного тренда.
В этом случае предполагается, что прогноз может
быть получен в виде выражения
где
- текущие оценки коэффициентов
адаптивных полиномов первой степени.
Согласно модели Хольта коэффициенты
полинома первой степени определяются
выражениями вида
где α1, α2 – параметры экспоненциального
сглаживания (α1 > 0; α2 <1)
Для того чтобы получить прогноз по модели
Хольта, нужно провести некоторую
подготовительную работу, а именно – рассчитать
значения начальные значения коэффициентов
адаптивных полиномов первой степени a1,0 и a2,0
при t=0 по имеющемуся ряду данных.
После этого по какому-либо критерию
подбираются постоянные сглаживания α1, α2 в
результате чего исследователь получает
линейную модель, на каждом шаге
адаптирующуюся к фактическим данным.
• Недостатком модели Хольта является
невозможность учета сезонности.
• Модель Хольта-Уинтерса является
развитием модели Хольта, в ней появляется
сезонная составляющая, в результате чего
получается система уравнений с тремя
постоянными сглаживания
• Модель с линейным трендом и учетом
сезонности может быть записана в виде
xˆ t   aˆ1,t    aˆ 2,t  fˆt l  ,
aˆ1,t
aˆ 2,t
xt
 1
 1  1   aˆ1,t 1  aˆ 2,t 1 ,
fˆt l
  3 aˆ1,t 1  aˆ 2,t 1   1   3 aˆ 2,t 1
ˆf   xt 
t
2
aˆ1,t l
где 0< α1, α2, α3 <1
• Оптимальные параметры α1, α2, α3 Уинтерс
предлагает находить экспериментальным
путем. Критерием сравнения он берет
стандартное отклонение ошибки. При этом
предполагается, что прогноз не смещен.
Поиск, осуществлялся с помощью сетки
значений α1, α2, α3.