лек-2
реклама

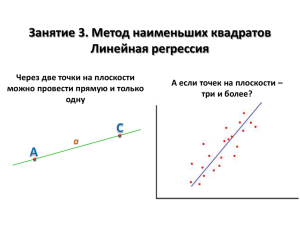
Парная линейная корреляция Метод наименьших квадратов • Задача: найти оценки параметров a и b такие, что i yi y xi 2 min i yi y xi • i остаток в i-ом наблюдении (отклонение наблюдаемого значения от прогнозируемого моделью) МНК (продолжение) S i yi y xi y a b x 2 2 i Необходимые условия экстремума: n a b x y 2 a x b x y x система нормальных уравнений МНК (продолжение) • Решение системы нормальных уравнений b covx, y 2 x yx y x x x 2 a y b x • где cov (х, у) — ковариация признаков 2 • x — дисперсия признака х 2 Интерпретация уравнения регрессии • b – коэффициент регрессии • Показывает среднее изменение результата с изменением фактора на одну единицу • a – может не иметь экономического смысла Пример: функция потребления • C=K·y+L • С — потребление • у - доход • K и L - параметры функции • y = C+I - r • I - размер инвестиций • r — сбережения Пример (продолжение) • Предположим: доход расходуется только на • потребление и инвестиции • • Пусть • тогда C K y L yCI C 1,9 0,65 y I 1,9 0,35 y К≤ 1 Адекватность модели • Наличие связи между переменными • Оценка значимости уравнения в целом – Анализ дисперсии – F-критерий Фишера • Выдвигается нулевая гипотеза H0: – коэффициент регрессии равен нулю, т. е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у. • Оценка значимости коэффициентов модели Теснота связи • Показатель тесноты связи rxy x covx, y yx y x rxy b y x y x y • Коэффициент детерминации r 2 yx 2 y объясн 2 y общ Анализ дисперсии y y 2 • Общая сумма • квадратов • отклонений • 2 = yx y + = Сумма квадратов отклонений объясненная регрессией • Показатель адекватности 2 xy r + 2 y yx Остаточная сумма квадратов отклонений Число степеней свободы (df— degrees of freedom) • df - число свободы независимого варьирования признака y y 2 2 2 yx y y yx n 1 1 (n 2) дисперсии на одну степень свободы y y 2 Dобщ Dфакт Dост n 1 2 yx y 1 2 y yx n2 F-критерий • Нулевая гипотеза H 0 : Dфакт Dост • F-отношение F Dфакт Dост Вывод по F-критерию • Fфакт > Fтабл H0 отклоняется • Fфакт < Fтабл уравнение регрессии считается статистически незначимым и Н0 не отклоняется • Величина F-критерия связана с 2 коэффициентом детерминации rxy 2 r F (n 2) 2 1 r доказательство 2 2 2 y x y r y n 2 2 2 y y x (1 r ) y n Пример: по группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек . № предприятия 1 2 3 4 5 6 7 Итого Выпуск продукции, тыс. ед. (х) 1 2 4 3 5 3 4 22 Затраты на производство, млн руб. (у) 30 70 150 100 170 100 150 770 ух x2 y2 30 140 600 300 850 300 600 2820 1 4 16 9 25 9 16 80 900 4900 22500 10000 28900 10000 22500 99700 yx 31,1 67,9 141,6 104,7 178,4 104,7 141,6 770,0 Пример (продолжение) • Система нормальных уравнений будет иметь вид 7a 22b 770 22a 80b 2820 • Тогда а = - 5,79; b= 36,84. • Уравнение регрессии y x 5,79 36,84 x • r2 = 0,982 Пример (продолжение) • общая сумма квадратов y y 2 y 2 n y 2 99700 7 110 2 15000 • факторная сумма квадратов 2 2 2 2 y y b x x 36 , 84 80 7 22 / 7 14735 x • остаточная сумма квадратов 2 y y x 15000 14735 265 Пример (продолжение) Dфакт 14735 Dостат 265 / 5 53 F 14735 / 53 278 F 0, 05 6,61; F 0, 01 16,26 • Вывод: уравнение регрессии значимо Fфакт >Fтабл Дисперсионный анализ результатов регрессии Источники вариации Число степеней свободы Сумма квадратов отклонений Общая 6 1 5 0 0 0 О б ъ я с н е н н а я 1 1 4 7 3 5 О с т а т о ч н а я 5 2 6 5 Дисперсия на одну степень свободы F-отношение фактическое табличное при α=0,05 - 1 4 7 3 5 5 3 53 mb 2,21 10,857 36,84 tb 16,67 t табл 2,57 2,21 - - - - 2 7 8 6 ,6 1 1 - -