прямая-урок1
реклама

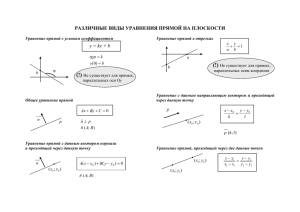
Урок1 Прямая на плоскости. Виды уравнений прямой на плоскости. Прямая на плоскости может быть задана одним из следующих ниже уравнений. 1. Прямая на плоскости однозначно задается точкой и вектором, перпендикулярным к этой прямой. Такой вектор называется нормальным вектором. М0(x0, y0) L Пусть М0(x0, y0) –точка, лежащая на прямой L; а вектор – нормальный вектор прямой L. Тогда для любой точки М(x, y), лежащей на этой прямой, вектор будет перпендикулярен вектору , а значит, их скалярное произведение должно быть равно нулю: A(x – x0)+B( y – y0) = 0 − уравнение прямой, проходящей через точку M0(x0, y0) перпендикулярно вектору 2. Выведем из полученного выше уравнения общее уравнение прямой: Пусть A(x – x0)+B( y – y0) =0. Раскроем скобки: Ax+By+(−A x0−B y0) = 0. Обозначим (–Ax0 – By0) = C, тогда получаем Ax + By + C = 0 – общее уравнение прямой на плоскости, где коэффициенты А, В - координаты нормального вектора. 3. Если С 0, то можно из общего уравнения прямой Ax + By + С = 0 получить уравнение прямой «в отрезках». Разделим общее уравнение Ax + By = –С на коэффициент (–С): Обозначим: тогда уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых прямой от координатных осей. Например, Y X 4. Если В 0, то можно получить уравнение прямой с угловым коэффициентом. Из общего уравнения Ax + By + C = 0 выразим y через x: By = –Ax – C; Y Обозначим тогда b O y = kx + b – уравнение прямой с угловым коэффициентом, где k – угловой коэффициент прямой, или тангенс угла между прямой и положительным направлением оси ОХ , k = tg; b – ордината точки пересечения прямой с осью OY. X Если угол - острый угол, то k>0, если угол - тупой , то k<0, если =0 прямая параллельна оси ОХ и k=0, если = / 2, то прямая не имеет углового коэффициента. 5. Прямая на плоскости также однозначно задается точкой и вектором, параллельным этой прямой. Такой вектор называется направляющим. М0(x0, y0) L Пусть М0(x0, y0) – точка, лежащая на прямой L; а вектор – направляющий вектор этой прямой. Тогда для любой точки М(x, y), лежащей на этой прямой, вектор будет коллинеарен вектору ,а следовательно, координаты векторов пропорциональны: будут Получили каноническое уравнение прямой, проходящей через точку М(x0, y0) параллельно направляющему вектору 6. Получим из канонического уравнения прямой параметрические уравнения, введя параметр t: параметрическое уравнение прямой, проходящей через точку М(x0, y0) параллельно вектору 7. Из параметрических уравнений получим уравнение прямой в векторном виде. Пусть радиус-вектор произвольной точки M, лежащей на прямой, радиус-вектор фиксированной точки M0, лежащей на прямой, направляющий вектор, - уравнение прямой в векторном виде. 8. Найдем уравнение прямой L, проходящей через 2 точки А(x1, y1) и B(x2, y2) на плоскости. Тогда – направляющий вектор этой прямой, а точка A(x1, y1) L. B А B A L B Для любой точки М(x, y), лежащей на прямой L, векторы и должны быть коллинеарны, а значит, их координаты должны быть пропорциональны: Получили уравнение прямой, проходящей через точки A и B. 9. Нормальное уравнение прямой. Пусть р − расстояние от прямой до начала координат, α − угол, образуемый перпендикуляром к прямой и положительным направлением оси ОХ. Точка M(x,y) - произвольная точка , лежащая на прямой. Через начало координат проведем n прямую перпендикулярно к данной. Точка P − точка пересечения этих прямых Y K X нормальное уравнение прямой, где cosα, cosβ – направляющие косинусы нормального вектора, направленного из начала координат в сторону прямой, а p (p>0) – расстояние от начала координат до прямой.