Лекция № 3 Направление процессов в физико-химических системах (часть 2)
реклама

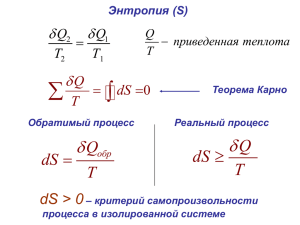
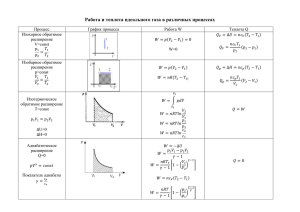
Лекция № 3 Направление процессов в физико-химических системах (часть 2) Направление процессов в физико-химических системах H=U+p·V • Энтальпия S = R · lnW • Энтропия (от греч. «преобразование») • W – вероятность макросостояния • S – мера беспорядка, связанная с вероятностью состояния. • Самопроизвольные процессы с ΔH < 0 Fe2O3 + 2Al = 2Fe + Al2O3 Плазма → атомы → молекулы → ассоциаты → кластеры → → кристаллы • Самопроизвольные процессы с ΔS > 0 Растворение солей (KMnO4 + H2O) Образование дефектов в кристаллах Самозагрязнение ОЧ веществ • Процессы вопреки условию ΔH < 0 (N2O4 → 2NO2, ΔH > 0 ) ΔS > 0 (кристаллизация солей из пересыщенных растворов, ΔS < 0) Энтальпийные и энтропийные факторы, обуславливающие самопроизвольность протекания физико-химических процессов – стремление к уменьшению энтальпии (ΔH < 0) и стремление к увеличению энтропии (ΔS > 0) В реальных условиях действуют оба фактора, которые можно сопоставить друг с другом количественно, выразив их в одинаковых единицах ΔH (Дж/моль), ΔS (Дж/К · моль) ΔH ~ Т ΔS ΔH = Т·ΔS Равновесное состояние системы Все возможные состояния системы ΔH ≶ Т·ΔS 1) ΔH < 0, ΔS > 0 - самая благоприятная ситуация 2) ΔH > 0, ΔS < 0 - самая неблагоприятная ситуация 3) ΔH > 0, ΔS > 0 - процесс может протекать при ΔH < Т·ΔS 4) ΔH < 0, ΔS < 0 - процесс может протекать при ΔH > Т·ΔS Абсолютное значение энтропии веществ, являющихся участниками физикохимического процесса, можно установить на основе измерений теплоемкости. По определению (3.1) Сp С p a bT cT Qp S 2 (3.2) (3.3) При нагреве исследуемого вещества от Т до Т + ΔT и р = const из (3.1) следует, что поглощаемая им теплота (3.4) Q p C p Подставляя (3.4) в уравнение (3.3), находим S C p В калориметре измеряем Cp от 0ºК до Т или Сp T1 T2 Т T При суммировании площади под кривой , находим S S C p ,i i C p d (3.5) Если в исследуемом интервале температур имеют место полиморфные превращения, плавление и кипение вещества, то на кривой наблюдаются соответствующие разрывы, отвечающие S полим орф полим орф полим орф пл кип ; S пл ; S кип пл кип Далее S0 → 0 при Т → 0 К (закон Планка) T Tкип С р (г) T dT S полим орф S пл S кип S ΔSпл ΔSполиморф Т1 ΔSкип г ж Т2 0 Т Температурная зависимость Т↑, S↑ ф.п., S↑ III з.т. ΔU = Q – A (3.6) A = Aмех + Aхим (3.7) ΔU = Q – Aмех – Aхим (3.8) Если О то При р = const ΔU = (Qp – p·ΔV – Aхим)p (3.9) Так как Qp = ΔΗ = T·ΔS (3.10) то ΔU = (T·ΔS - p·ΔV - Aхим )р (3.11) Или -Aхим = (ΔU + p·ΔV – T·ΔS)р (3.12) При Т = const -Aхим = Δ(U + p·V – T·S)р,T Z Изобарно–изотермический потенциал (3.13) G -энергия Гиббса или химический µ Z ≡ G ≡ µ = U + pV – TS = H – TS Из (3.13) и (3.14) -Ахим = ΔGp,T ≡ Δµ где ΔG = ΔΗ – T·ΔS (3.14) (3.15) (3.16) ΔG как критерий самопроизвольного процесса ΔG < 0 – реакция идет самопроизвольно ΔG > 0 – реакция невозможна ΔG = 0 – равновесие Чем больше ΔG, тем дальше система от состояния равновесия ΔΗ ΔU Т · ΔS р · ΔV ΔG (≡ Δµ) Свойства «свободной энергии» Абсолютное значение неизвестно (U!) Является функцией состояния (комбинация параметров системы U, S, T, p, V) ΔG = G2 – G1 (p = const, T = const) r G i i Gпрод.( i ) j G реаг.( j ) j Может быть применена к неизолированной системе в условиях, удобных для рассмотрения химических реакций Объединяет энергетические и энтропийные характеристики Джозайя-Уиллард Гиббс (Gibbs J. W.) 11.II.1839 - 28.IV.1903