Об управлении рынками электроэнергии как макросистемами
реклама
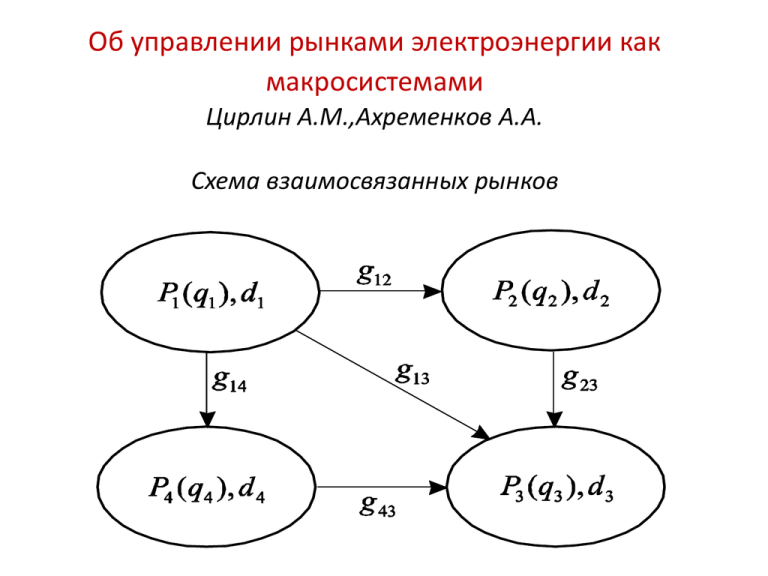
Об управлении рынками электроэнергии как макросистемами Цирлин А.М.,Ахременков А.А. Схема взаимосвязанных рынков • Задачи оптимального распределения генерации электроэнергии на протяжении десятилетий находились в центре многих исследований. При этом стоимость генерации, являвшаяся целевой функцией в классических задачах оптимального распределения, как правило предполагалась непрерывной и непрерывно дифференцируемой. Изложенный алгоритм учитывает влияние ступенчатого характера ценовых заявок на рыночную стоимость генерации и невыпуклость задачи распределения, связанную с тем, что заявки предполагают отрицательные цены. Региональная ценовая заявка --зависимость цены Pi от суммарного объема энергии, предложенного поставщиками данного региона по цене, не превышающей Pi • Здесь Gi– число региональных поставщиков энергии, а Pi(g)– их ценовые заявки . G qi i 1 i i maxPi ( ) Pi Постановка задачи . Зависимость потерь энергии от величины межрегиональных потоков Баланс энергии для сети описывается уравнением n n 1 n qi d i Lij ( gij ) 2 i j 1i j i 1 i 1 Баланс сети выполняется, если выполнены региональные балансы n qi di ( gij ij Lij ( gij )) i 1… n j 1 • Стоимость генерации на i-м рынке описывается соотношением qi Ci ( qi ) Pi ( x )dx 0 dCi Pi ( qi ) dqi Общая стоимость генерации определяется как n I (d1… d n qi … qn ) Ci ( qi ) i 1 Формальная постановка I ( d1 … d n qi … qn ) minqi gij • с учетом автономных ограничений: q qi q i 1… n min i max i g gij g j 1… n min ij max ij i 1… n и балансов региональных рынков Общее число неизвестных задачи равно n n n(n 1) n 2 2 2 Общее число связей равно n n 0 Необходимые условия оптимальности dLij dLij 1 ij Pi 1 ji dg dg ij ij Здес ь Pj Pj Pj (q j ) Pi Pi ( qi ) и — цены, соответствующие выбранным суммарным объемам поставок в ценовых заявках для регионов. Назовем в этих уравнениях величины, стоящие в левой и правой частях равенства, скорректированными ценами Автоматическая оптимизация распределения поставок энергии Условия оптимальности могут быть использованы для создания непрерывных автоматических систем управления рынком электроэнергии, в которых последовательность периодических аукционов можно заменить одним непрерывным аукционом. Это позволит значительно снизить уровень ошибок при расчете оптимального распределения поставок. Рассмотрим сеть региональных рынков как экономическую макросистему [6], состоящую из подсистем (региональных рынков), которые обмениваются ресурсом — энергией. Система является открытой, так как она получает внешние потоки заявок от потребителей и производителей энергии. В каждой подсистеме имеется своя оценка энергии , которая, в свою очередь, зависит от объемов обмена между подсистемами . РАВНОВЕСИЕ В ОТКРЫТОЙ МАКРОСИСТЕМЕ Согласно принципу Пригожина в термодинамических системах производство энтропии (рассеяние энергии) в стационарном режиме минимально sign[ gij ( Pi Pj )] sign[ Pi Pj ] • Потоки энергии в такой системе направлены в сторону регионов с более высокой энергетической оценкой, что приводит к снижению последних и сближению оценок на всех рынках в СТАЦИОНАРНОМ режиме. Когда энергия передается в j-й региональный рынок (gij>0), то количество энергии , генерируемое на этом рынке, уменьшается; соответственно уменьшаЮтся стоимость генерации и наивысшая ценовая ступенька на ценовой заявке g ij Выберем кинетические функции (функции перетока) так, чтобы для них стационарное состояние системы удовлетворяло условиям оптимальности. Условия равенства скорректированных цен можно записать в форме функционального уравнения относительно функции перетока g ij Pi ij ( gij ) i j 1… n i j gij g ji Pj Или dLij 1 (1 ij ) L Pi L( gij ) где 1 ij L Pj dgij Получим зависимость кинетической функции от функции потерь в сетях L( gij ) Pj Pi Pij Pij ij Pi ji Pj Для квадратичной функции потерь Lij ( gij ) ij g 2 ij 1 gij ( Pi Pj ) Pj Pi 2ij Pij Для линейно-квадратичной функции потерь Оптимальная кинетическая функция имеет вид показанный на рисунке • Характер зависимости оптимального потока в сети от разности наивысших цен поставки на двух региональных рынках. Если получена зависимость g ij или ее аппроксимация для всех i,j, то решение задачи распределения поставок значительно упрощается, поскольку она распадается на отдельные задачи управления потоками в реальном времени: • — измерение заявок потребителей в реальном времени, • — пересчет региональных цен по известным ценовым заявкам генераторов, • — изменение потоков в зависимости от вида аппроксимации функции потерь в соответствии с найденной кинетической функцией • Эти задачи решает система управления с обратной связью, поддерживающая условия оптимальности. Заключение • Задача управления на взаимосвязанных рынках электроэнергии сводится к оптимизации перетоков между рынками, так чтобы средняя цена поставки была минимальна при ограничениях, связанных с возможностями генерации и сетей. Показано, что систему рынков можно рассматривать как макросистему, равновесное состояние которой при определенном выборе зависимости потоков обмена от региональных цен удовлетворяет условиям оптимальности.






