Лекция 5. Кручение
реклама

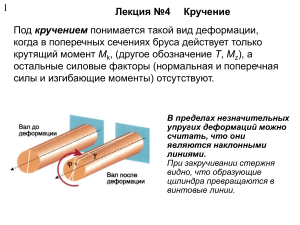
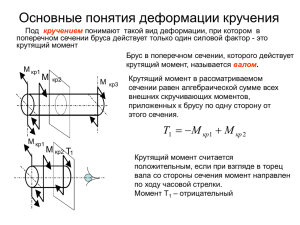
Лекция 5. Кручение Кручение – это вид деформации, характеризующийся взаимным поворотом поперечных сечений под действием крутящих моментов, действующих в этих сечениях. При кручении в поперечных сечениях возникают только внутренние крутящие моменты. Mx 0 Остальные пять силовых факторов равны нулю. Кручение круглого вала. Правило знаков Рассмотрим вал, нагруженный системой внешних крутящих моментов и находящийся в равновесии. M4 M2 X M3 M1 Кручение. Метод сечений M4 M2 Mx X X Mx M3 x Запишем условие равновесия левой части вала: M4 M3 M2 M x 0 ; M x M 4 M 3 M 2 M1 , так как вал находится в равновесии, т.е. M 4 M 3 M 2 M1 0 M1 Построение эпюр крутящих моментов Практическое правило. Крутящий момент M x в любом поперечном сечении вала равен алгебраической сумме внешних крутящих моментов, действующих с одной стороны от сечения, взятой с обратным знаком. Рассмотрим вал, находящийся в равновесии: m 4m 2m m 0 m 0 x1 4m x2 2m x3 m x4 x Построение эпюр крутящих моментов (продолжение) Воспользуемся практическим правилом. M x m M x m 4m 3m M x m 4m 2m m m 4m x1 0 Mx x2 2m x3 при при при m x4 x 3m m 0 0 x x1 x1 x x2 x 2 x x3 m x Напряжения и деформации при кручении Задача решается при следующих допущениях: 1. Вал остается прямолинейным. Его ось не искривляется. 2. Справедлива гипотеза плоских сечений: Поперечное сечение вала, нагруженного крутящими моментами, поворачивается в своей плоскости, как жесткий диск. Радиусы сечения не искривляются. 3. Расстояния между поперечными сечениями вала не изменяются, т.е. длина бруса при кручении остается неизменной. Система координат r t Mx x M1 Ось t - это касательная к окружности в точке пересечения радиуса с окружностью. Из принятых допущений следует, что все деформации, за исключением деформации сдвига xt , равны нулю. При кручении изменяются прямые углы между направлениями x и t xt tx 0 . xt tx 0 Кольцевой элемент Двумя плоскостями, нормальными к оси бруса, вырежем диск толщиной dx . Двумя соосными цилиндрическими плоскостями, d , вырежем из диска кольцо радиусом и отстоящими на толщиной d . d dx Деформация кольца bb xt dx d d xt . dx (5.1) Деформации и напряжения при кручении Введем относительный угол закручивания d dx . (5.2) Тогда xt . (5.3) Теперь, с учетом закона Гука xt G xt , запишем xt G . (5.4) Из уравнений (5.3) и (5.4) следует, что касательные напряжения xt и сдвиги xt прямо пропорциональны расстоянию рассматриваемой точки сечения. от оси вала до Деформации и напряжения, продолжение Вычисление крутящего момента в сечении dM x xt dF Суммарный крутящий момент равен M x xt dF G 2 dF GI p , F где Ip (5.5) F - полярный момент инерции сечения, равный I p 2 dF . F (5.6) Вычисление угла закручивания вала d M x , dx GI p (5.7) GI p - жесткость сечения при кручении. L M x dx , GI p 0 M xL GI p . (5.8) (5.9) Вычисление напряжений при кручении xt M x G Ip Mx xt . Ip (5.10) Mx max M x xt R Ip Wp , (5.11) Wp - полярный момент сопротивления кручению Wp Ip R . (5.12) Эпюра касательных напряжений Полярные моменты инерции dF 2d R I p dF 2 d 2 F Wp Ip R Для трубы 0 3 R 2 3 R 4 2 D 4 (5.13) . 32 D 3 16 I p (5.14) . D4 d 4 W p 32 , D4 d 4 16 D (5.15) . (5.16) Условный предел текучести при кручении xt 0,3 D D 0,3 0,3 0,3 2 2 L 6 L 3 10 D 0,3 0,3 0,003 M 0,3 Wp . Расчет на прочность и жесткость при кручении Расчет на прочность 0,3 n max Расчет на жесткость или , и где - допускаемый в конструкции абсолютный или относительный угол закручивания. Кручение эллиптического вала a b Напряжения при кручении эллиптического вала – трехмерный график T Напряжения при кручении эллиптического вала – контурный график T Кручение вала прямоугольного сечения a b Напряжения при кручении прямоугольного вала – трехмерный график T1 Напряжения при кручении прямоугольного вала –контурный график T1