Кручение - Сопротивление материалов
реклама

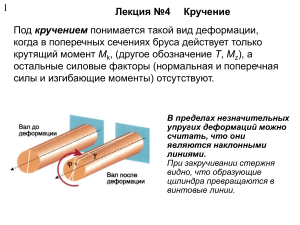
Основные понятия деформации кручения Под кручением понимают такой вид деформации, при котором в поперечном сечении бруса действует только один силовой фактор - это крутящий момент Брус в поперечном сечении, которого действует крутящий момент, называется валом. М кр1 М кр2 М кр3 Крутящий момент в рассматриваемом сечении равен алгебраической сумме всех внешних скручивающих моментов, приложенных к брусу по одну сторону от этого сечения. М кр1 T1 M кр1 M кр 2 М кр2 Т1 Крутящий момент считается положительным, если при взгляде в торец вала со стороны сечения момент направлен по ходу часовой стрелки. Момент Т1 – отрицательный Закон Гука при кручении Основные допущения: 1.Поперечные сечения вала, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси, и после деформации. 2.Радиусы поперечных сечений не искривляются и сохраняют свою длину. 3.Расстояния между поперечными сечениями не изменяются. При кручении наблюдается плоское напряженное состояние чистого сдвига и соблюдается закон Гука при сдвиге: G , Т Т d Рассмотрим особенности деформации бруса при кручении d dz d G G dz d dz В поперечных сечениях вала возникают касательные напряжения, направление которых, в каждой точке перпендикулярно к радиусу, соединяющему эти точки с центром сечения, а величина прямо пропорциональна расстоянию точки от центра. Напряженное состояние при кручении T 3 1 3 1 1 ; 2 0; 1 3 1 мин макс 3 3 1 Возможны следующие варианты разрушения образцов Продольные трещины От действия главных напряжения в плоскости наклоненной под 450 к оси образца. Хрупкие материалы (чугуны, закаленные стали) От действия касательных напряжения в плоскости поперечного сечения Пластичные материалы От действия касательных напряжений в плоскости параллельной образующей Анизотропные материалы (древесина) Напряжения при кручении T Ip max max Полярный момент инерции характеризует, влияние размеров и форма поперечного сечения вала на его способность сопротивляться угловым деформациям 4 4 Ip d 4 32 , Для круглого сечения Ip d 1 2 d /2 3 d I p 0 Для трубчатого сечения 32 здесь a = d1 /d, d1 –внутренний диаметр трубы, d – наружный диаметр трубы Полярный момент инерции выражается в м4 (мм4, см4). Полярный момент сопротивления характеризует влияние геометрических размеров и формы поперечного сечения вала на его прочность. Wp d 3 16 Для круглого сечения Wp d 3 1 4 16 Wp Ip макс Для трубчатого сечения Максимальные касательные напряжения max прямо пропорциональны крутящему моменту T в опасном сечении и обратно пропорциональны полярному моменту сопротивления сечения Wp: max T Wp Условие прочности при кручении Наибольшие касательные напряжения, возникающие в скручиваемом брусе не должны превышать соответствующих допускаемых значений по 3 теории прочности кр T 2 Допускаемые макс кр Wp напряжения по 4 теории прочности кр 3 Из условия прочности вытекает три типа задач при кручении . Задача проектного расчета d 3 d 3 . Задача проверочного расчета . Определение допускаемого момента 16Tм акс р 16Tмакс 1 4 р Tмакс кр Wp T кр W p Для круглого сечения Для трубчатого сечения Деформации при кручении. Условие жесткости при кручении При кручении различают угол закручивания и относительный угол закручивания G G Закон Гука при кручении Напряжения при кручении T Ip Угол закручивания Условие жесткости при кручении. T GI p Tl GI p Наибольший относительный угол закручивания, возникающий в скручиваемом брусе не должен превышать соответствующих допускаемых значений max Где [] – допускаемы относительный угол закручивания. []=0,0045….0,02 рад/м Потенциальная энергия деформации T T Tl T 2l U 2 2 GI p 2GI p Полная потенциальная энергия деформации Удельная потенциальная энергия (полная) 1 u 12 22 32 2 1 2 2 3 1 3 2E 1 1 2 2 2 u 2 2 2E E Удельная потенциальная энергия изменения объема 1 2 2 uV 1 22 32 6E Удельная потенциальная энергия изменения формы 1 2 1 22 32 1 2 2 3 3 1 3Е 1 1 2 2 2 3 2 3 1 2 6Е 1 1 2 uф 2 2 2 3E E 2 0; 3 uф При кручении 1 ;