Алгебра логики 1
реклама

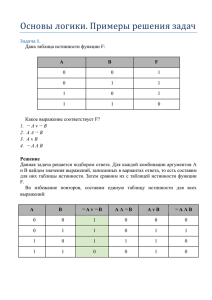
Основы математической логики Логические переменные. Логические функции. Основные понятия Математическая логика - это наука о методах рассуждений, при которых мы отвлекаемся от содержания рассуждений, а используем только их форму и значение. В математической логике мы будем использовать только логические переменные, которые принимают значения либо 0 ("ложь"), либо 1 ("истина"). Функции, которые определены на этих переменных и принимают значения 0 или 1 также называются логическими. Основные понятия Наборы, на которых задана функция, могут быть представлены в виде конституэнтов, двоичных или десятичных эквивалентов. Конституэнтом называется логическое произведение переменных или их отрицаний в виде n i & xi , где i 1 i xi x xi x при при i 1 i 0 i Основные понятия Двоичные эквиваленты формируются из значений Например, конституэнту x1 x2 x3 соответствует двоичный набор 001, а конституэнту x1 x x3 101. Десятичные эквиваленты легко могут быть получены из двоичных с помощью степенного ряда: 001 0 2 2 0 21 1 20 1 101 1 2 2 0 21 1 20 5 i Логические функции и таблицы истинности Основные логические функции Значения переменных любой логической функции могут принимать только 0 и 1. При N переменных существует 2 различных наборов переменных. N Значение самой логической функции тоже может быть только 0 или 1 («ложь» или «истина»), следовательно различных логических функций 2N от N переменных может быть 2 Для функций с двумя переменными известны 16 логических функций: логическое сложение +, или дизъюнкция V; логическое умножение, или конъюнкция &; отрицание (по первой переменной) a ; отрицание (по второй переменной) b ; импликация, или функция следования – левая → и правая ←; сложение по модулю 2 или жегалкинское сложение ; функция Шеффера |; Для функций с двумя переменными известны 16 логических функций: стрелка Пирса ↓, или функция Вебба °; обратная импликация, или коимпликация – левая → и правая ← ; функция тождества, или эквивалентность ~; единичная функция 1; нулевая функция 0; функция сохранения первой переменной a; функция сохранения второй переменной b. Таблицы истинности Логическое сложение а + b, или дизъюнкция а V b Дизъюнкция двух слагаемых ложна тогда и только тогда, когда ложны оба слагаемых. a b a+b 0 0 0 0 1 1 1 0 1 1 1 1 Таблицы истинности Логическое умножение а • b, или конъюнкция а & b Конъюнкция двух сомножителей истинна тогда и только тогда, когда истинны оба сомножителя a b a·b 0 0 0 0 1 0 1 0 0 1 1 1 Таблицы истинности a Отрицание Отрицание лжи есть истина, отрицание истины есть ложь. a a 0 1 1 0 Таблицы истинности Функция отрицания может быть не только от одной переменной. Например, отрицание первой переменной выглядит следующим образом: a b a ( a, b) 0 0 1 0 1 1 1 0 0 1 1 0 a ( a, b) a В данной записи функция не зависит от второй переменной b, которая считается несущественной. Таблицы истинности Отрицание второй переменной выглядит следующим образом: a b b ( a, b ) 0 0 1 0 1 1 1 0 0 1 1 0 b (a, b) b В данной записи функция не зависит от второй переменной а, которая считается несущественной. Таблицы истинности Импликация или функция следования: левая а→b и правая a←b Для функции импликации из лжи следует все что угодно, а из истины только истина. a b a→b a b a←b 0 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 0 1 1 1 1 1 1 1 a b a b a b ab Таблицы истинности Сложение по модулю 2 a b Функция сложения по модулю 2 истинна тогда и только тогда, когда значения переменных различны. a b a b 0 0 0 0 1 1 1 0 1 1 1 0 a b a b ab Таблицы истинности Функция тождества, или эквивалентность а ~ b Функция истинна тогда и только тогда, когда значения переменных совпадают. a b a~b 0 0 1 0 1 0 1 0 0 1 1 1 Функция эквивалентности противоположна сложению по модулю 2, и для нее справедливо a b a b a b ab Таблицы истинности Функция Шеффера а | b Функция ложна тогда и только тогда, когда оба значения переменных истинны. a b а|b 0 0 1 0 1 1 1 0 1 1 1 0 Функция Шеффера противоположна конъюнкции, и для нее справедливо а|b= a b a b Таблицы истинности Стрелка Пирса а ↓ b, или функция Вебба а °b Функция истинна тогда и только тогда, когда ложны обе ее переменные. a b а↓b 0 0 1 0 1 0 1 0 0 1 1 0 a b a b a b Таблицы истинности Единичная функция 1 Данная функция определяет логическую константу 1. a b 1 0 0 1 0 1 1 1 0 1 1 1 1 1(а, b)=1 Таблицы истинности Нулевая функция О Данная функция определяет логическую константу 0. a b 0 0 0 0 0 1 0 1 0 0 1 1 0 0(а, b) = 0 Таблицы истинности Функция сохранения первой переменной а Данная функция истинна тогда и только тогда, когда переменная а истинна. a b a 0 0 0 а(а, b) = а 0 1 0 1 0 1 1 1 1 Таблицы истинности Функция сохранения второй переменной b Данная функция истинна тогда и только тогда, когда переменная b истинна. a b b 0 0 0 b(a, b) = b 0 1 1 1 0 0 1 1 1 Задачи Определить значения, которые принимают следующие логические функции при заданных значениях переменных 1. а —>b = ? при а = 0, b = 1. 2. a b ? при а = О, b =0. 3. a Ib = ? при а = 1, b = 0. 4. a ↓b = ? при а =1, b = 1. 5. a b = ? при а = 1, b = 0. 6. a —>b = ? при а = 1, b = 1. 7. a b ? при а = 0, b =0. 8. а~b = ? пpu a = 0, b = 1. 9. a b ? при а = 1, b = 0. Проверь себя Задача Составить таблицу истинности для функции: F ( x1 , x2 , x3 ) ( x1 x2 ) x3 Решение Определим значение наборов переменных. Их восемь - 000, 001, 010, 011, 100, 101, 110, 111. Каждому из них можно поставить в соответствие десятичный эквивалент (0, 1,......, 7). Построим таблицу истинности рассматриваемой функции. На 1-м шаге выписываем значения наборов переменных x1 x2 x3 000 001 010 011 100 101 110 111 Построим таблицу истинности рассматриваемой функции. На 2-м шаге определяем порядок выполнения элементарных функций и заполняем ими заголовки столбцов x1 x2 x3 000 001 010 011 100 101 110 111 x1 x2 x3 ( x1 x2 ) x 3 Построим таблицу истинности рассматриваемой функции. На 3-м шаге вычисляем значения функции x1 x2 x3 x1 x2 000 1 001 1 010 1 011 1 100 0 101 0 110 1 111 1 x3 x1 x2 ( x1 x2 ) x 3 Построим таблицу истинности рассматриваемой функции. На 4-м шаге вычисляем значения x 3 x1 x2 x3 x1 x2 x3 000 1 1 001 1 0 010 1 1 011 1 0 100 0 1 101 0 0 110 1 1 111 1 0 ( x1 x2 ) x 3 Построим таблицу истинности рассматриваемой функции. На 5-м шаге вычисляем значения ( x1 x2 ) x 3 x1 x2 x3 x1 x2 x3 000 1 1 ( x1 x2 ) x 3 1 001 1 0 0 010 1 1 1 011 1 0 0 100 0 1 1 101 0 0 1 110 1 1 1 111 1 0 0 Задачи Построить таблицы истинности для функций: 1.(a b) c; 2.(a b ) c; 3.(a b) c; 4.a b a b ; 5.(a b ) (a b); 6.a b c ; 7.(a b) (d c). Ответы Задание 1 abc 1 2 000 1 1 001 1 0 010 1 1 011 1 0 100 1 1 101 1 0 110 0 1 111 0 1 Ответы Задание 2 abc 1 2 3 000 1 1 0 001 1 1 1 010 0 0 0 011 0 0 0 100 1 0 0 101 1 0 0 110 0 1 0 111 0 1 1 Ответы Задание 3 abc 1 2 3 4 000 1 0 1 0 001 1 0 1 1 010 1 1 0 1 011 1 1 0 1 100 0 1 0 1 101 0 1 0 1 110 0 1 0 1 111 0 1 0 1 Ответы Задание 4 abc 1 2 3 4 5 000 0 1 1 1 1 001 0 1 1 1 1 010 0 1 0 0 0 011 0 1 0 0 0 100 0 0 1 0 0 101 0 0 1 0 0 110 1 0 0 0 1 111 1 0 0 0 1 Ответы Задание 5 abc 1 2 3 4 5 000 1 1 1 1 1 001 1 1 1 1 1 010 0 0 1 1 0 011 0 0 1 1 0 100 1 1 0 0 0 101 1 1 0 0 0 110 0 1 0 1 1 111 0 1 0 1 1 Ответы Задание 6 abc 1 2 3 4 000 1 1 1 0 001 1 1 0 1 010 1 0 1 1 011 1 0 0 0 100 0 0 1 1 101 0 1 0 0 110 0 0 1 0 111 0 1 0 1 Ответы Задание 7 abcd 1 2 3 0000 1 1 0 0001 1 0 0 0010 1 0 0 0011 0 0 0 0100 0 1 0 0101 0 0 1 0110 0 0 1 0111 0 0 1 1000 0 1 0 1001 0 0 1 1010 0 0 1 1011 0 0 1 1100 0 1 0 1101 0 0 1 1110 0 0 1 1111 0 0 1