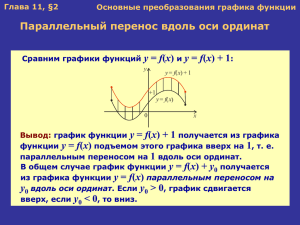
Тема «Построение графика функций y=
реклама
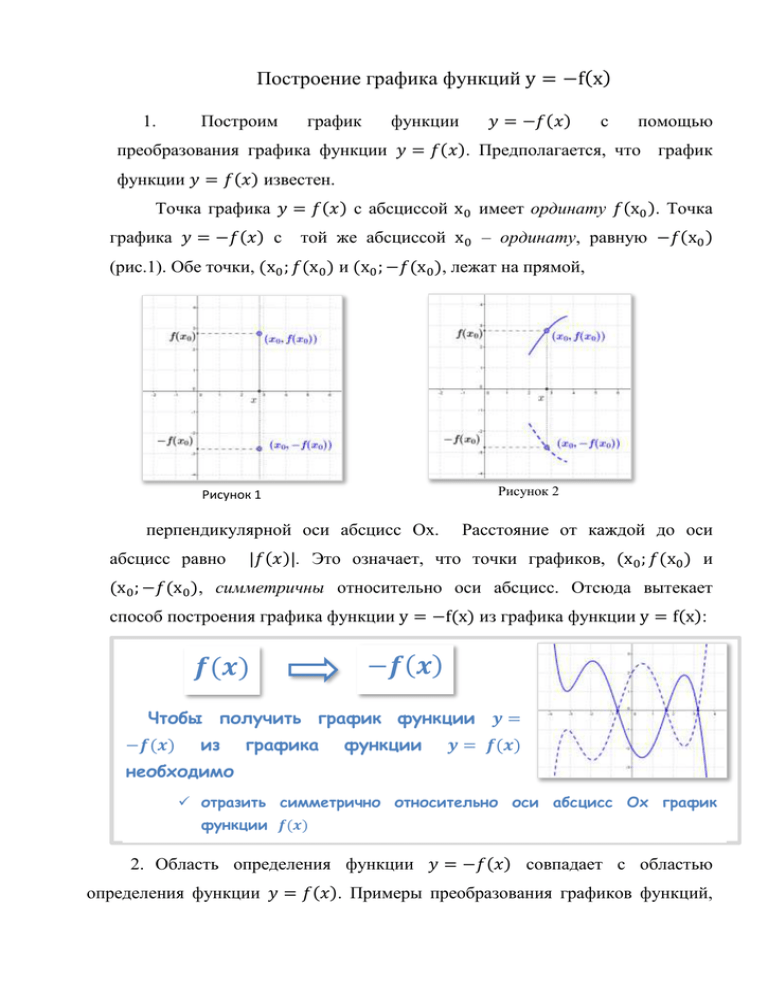
Построение графика функций y = −f(x)
1.
Построим
график
функции
𝑦 = −𝑓(𝑥)
с
помощью
преобразования графика функции 𝑦 = 𝑓(𝑥). Предполагается, что график
функции 𝑦 = 𝑓(𝑥) известен.
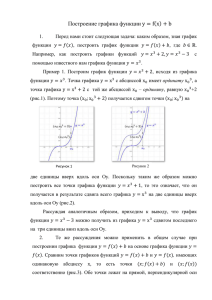
Точка графика 𝑦 = 𝑓(𝑥) с абсциссой x0 имеет ординату 𝑓(x0 ). Точка
графика 𝑦 = −𝑓(𝑥) с
той же абсциссой x0 – ординату, равную −𝑓(x0 )
(рис.1). Обе точки, (x0 ; 𝑓(x0 ) и (x0 ; −𝑓(x0 ), лежат на прямой,
Рисунок 2
Рисунок 1
перпендикулярной оси абсцисс Ox.
абсцисс равно
Расстояние от каждой до оси
|𝑓(𝑥)|. Это означает, что точки графиков, (x0 ; 𝑓(x0 ) и
(x0 ; −𝑓(x0 ), симметричны относительно оси абсцисс. Отсюда вытекает
способ построения графика функции y = −f(x) из графика функции y = f(x):
𝒇(𝒙)
−𝒇(𝒙)
Чтобы получить график функции 𝒚 =
−𝒇(𝒙)
из
графика
функции
𝒚 = 𝒇(𝒙)
необходимо
отразить симметрично относительно оси абсцисс Ox график
функции 𝒇(𝒙)
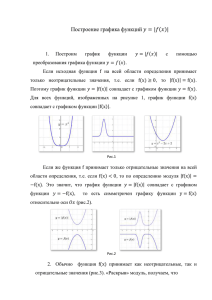
2. Область определения функции 𝑦 = −𝑓(𝑥) совпадает с областью
определения функции 𝑦 = 𝑓(𝑥). Примеры преобразования графиков функций,
изображенных на рисунках 3 и 4, показывают, что множества значений функций
𝑦 = √𝑥 и 𝑦 = −√𝑥 различаются. Так же как и функций 𝑦 = |𝑥| и 𝑦 = −|𝑥|. В
обоих случаях функция 𝐸(𝑓) = [0; ∞), а . 𝐸(−𝑓) = (−∞; 0].
Рисунок 4
Рисунок 3
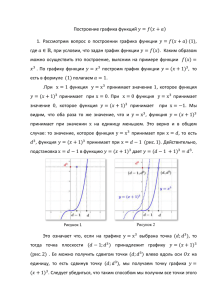
При симметрии относительно оси абсцисс вместе с графиком функции 𝑦 =
𝑓(𝑥) симметрично отражается и его проекция на ось Oy, то есть множество
значений функции. Поэтому, промежуток 𝐸(−𝑓) симметричен промежутку
𝐸(𝑓) относительно начала координат. В примере, изображенном на рисунке
5, 𝐸(𝑓) = [1; 3], а 𝐸(−𝑓) = [−3; −1].
Рисунок 5
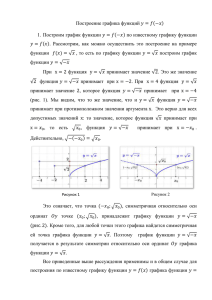
Если область значений функции 𝑦 = 𝑓(𝑥) – все действительные числа, то
E(−f) = E(f). Примеры приведены на рисунках 6 и 7.
Рисунок 6
Рисунок 7
Упражнения
1. Постройте график функции.
a) 𝑦 = 2 − |𝑥|
c) 𝑦 = −
1
𝑥
b) 𝑦 = 1 − √𝑥
𝑥 2 , если x < 0
d) 𝑦 = − {
√𝑥, если x ≥ 0
2. Для каких функций 𝑦 = f(x), заданных на всей числовой оси,
выполняется равенство f(x) = −f(x) при всех 𝑥 ∈ ℝ?
3. На рисунке изображен график функции y = f(x). Начертите
схематически график функции y = −f(x).
4. Найти область значений функции 𝑦 = −𝑓(𝑥), если известна область
значений функции 𝑦 = 𝑓(𝑥)
𝑬(𝒇)
[2; 5]
[1; ∞)
(−∞; −1] ∪ [1; ∞)
(−∞; ∞)
(−6; 2) ∪ (2; 3)