Тема «Построение графика функций y=|f(x)|».
реклама
Построение графика функций 𝑦 = |𝑓 (𝑥 )|
1.
Построим
график
функции
𝑦 = |𝑓(𝑥)|
с
помощью
преобразования графика функции 𝑦 = 𝑓(𝑥).
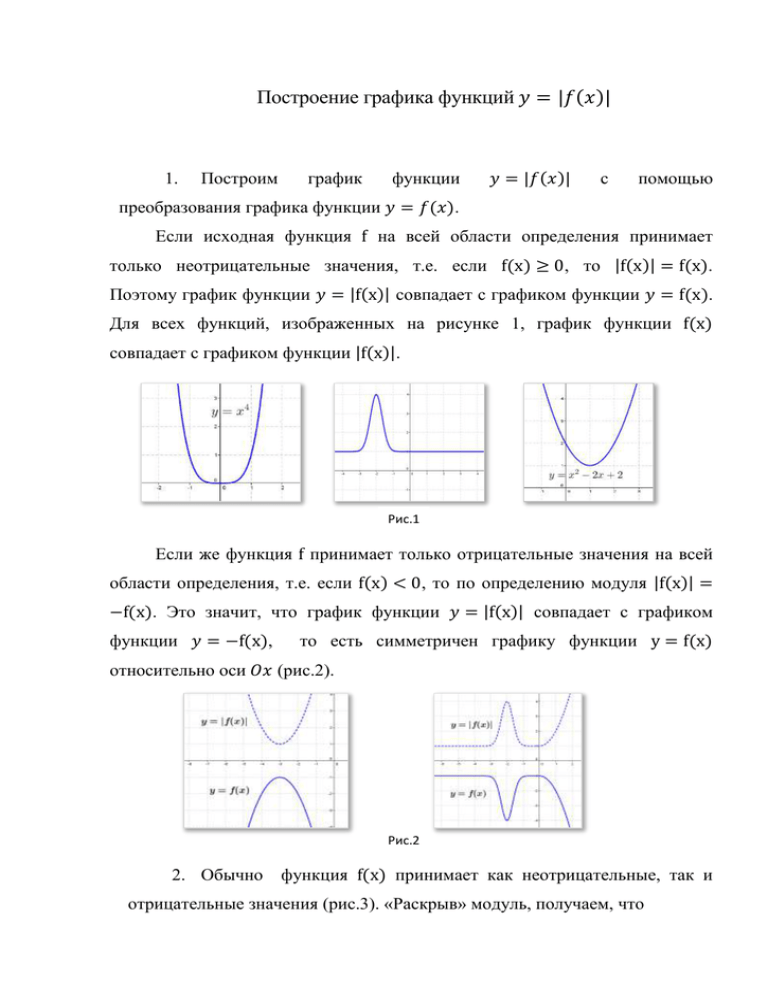
Если исходная функция f на всей области определения принимает
только неотрицательные значения, т.е. если f(x) ≥ 0, то |f(x)| = f(x).
Поэтому график функции 𝑦 = |f(x)| совпадает с графиком функции 𝑦 = f(x).
Для всех функций, изображенных на рисунке 1, график функции f(x)
совпадает с графиком функции |f(x)|.
Рис.1
Если же функция f принимает только отрицательные значения на всей
области определения, т.е. если f(x) < 0, то по определению модуля |f(x)| =
−f(x). Это значит, что график функции 𝑦 = |f(x)| совпадает с графиком
функции 𝑦 = −f(x),
то есть симметричен графику функции y = f(x)
относительно оси 𝑂𝑥 (рис.2).
Рис.2
2. Обычно функция f(x) принимает как неотрицательные, так и
отрицательные значения (рис.3). «Раскрыв» модуль, получаем, что
|𝑓(𝑥)| = {
𝑓(𝑥), если 𝑓(𝑥) ≥ 0
(1)
−𝑓(𝑥), если 𝑓(𝑥) < 0
Выполнение для некоторого значения аргумента 𝑥0 условия
𝑓(𝑥0 ) ≥ 0 означает, что точка графика (𝑥0 , 𝑓(𝑥0 )) лежит в верхней
полуплоскости, т.е. выше оси абсцисс или на самой оси. Для всех таких
значений аргумента, они на рисунке 3 обозначены сплошной линией,
выполняется равенство |f(x)| = f(x). Это означает, что для этих значений
аргумента график функции y = |f(x)| совпадает с графиком функции y =
f(x), или другими словами, все части графика функции 𝑦 = 𝑓(𝑥), лежащие
выше оси абсцисс, являются также частями графика функции y = |f(x)|.
Рис. 3
Теперь рассмотрим те значения аргумента функции 𝑦 = 𝑓(𝑥), при
которых функция принимает отрицательные значения, т.е. f(x) < 0. На
рисунке они обозначены пунктирной линией. Соответствующие этим
значениям аргумента части графика функции 𝑦 = f(x) лежат ниже оси
абсцисс. Из формулы (1) следует, что при f(x) < 0 выполняется равенство
|f(x)| = −f(x) и поэтому для рассматриваемых значений аргумента график
функции y = |f(x)| совпадает с графиком функции y = −f(x). График этой
функции симметричен графику функции y = f(x) относительно оси 𝑂𝑥.
Из вышесказанного вытекает способ построения графика функции 𝑦 =
|f(x)| исходя из графика функции y = f(x):
𝒇(𝒙)
|𝒇(𝒙)|
Чтобы получить график функции |𝒇(𝒙)|
из графика функции 𝒇(𝒙) необходимо:
оставить без изменений части графика функции 𝒇(𝒙), лежащие
выше оси абсцисс OX
отразить
симметрично
относительно
оси
абсцисс
OX
части
графика функции 𝒇(𝒙), лежащие ниже этой оси
Таким образом, последовательность построения графика функции 𝑦 =
|f(x)| исходя из графика функции y = f(x), будет выглядеть следующим
образом:
Рис. 3
Отметим, что область определения функции 𝑦 = |𝑓(𝑥)|
совпадает с
областью определения функции 𝑦 = 𝑓(𝑥), а множество значений составляет
множество чисел |𝑐|, где 𝑐 ∈ 𝐸(𝑓).
3. Пример 1. Построить график функции y = |x 2 − x − 2|.
Сначала построим график функции y = x 2 − x − 2 (рис.4). Затем
преобразуем его по описанному выше правилу: те
части
параболы,
которые лежат выше оси абсцисс Ox, оставим без изменений, а части,
лежащие ниже оси абсцисс, отразим симметрично относительно этой оси. В
результате получаем график функции y = |x 2 − x − 2| (рис.5).
Рис. 5
Рис. 4
Пример 2. Построить график функции y = ||x − 1| − 2|.
Используя правила построения графиков вида 𝑦 = 𝑓(𝑥) + 𝑏 и 𝑦 = |𝑓(𝑥)|,
последовательно построим графики функций y = 𝑥 − 1, y = |x − 1|, y =
|x − 1| − 2, y = ||x − 1| − 2| (рис.6).
b)
a)
Рис. 6
c)
d)
Упражнения
1. Постройте график функции.
a) 𝑦 = |2𝑥 − 1|
b) 𝑦 = |𝑥 2 − 2𝑥 − 3|
c) 𝑦 = |𝑥 3 |
d) 𝑦 = |1 − 𝑥|
e) 𝑦 = | − 𝑥 2 + 3|
f) 𝑦 =
1
|𝑥|
2.
На рисунке изображен график функции y = f(x). Начертите
схематически график функции y = |𝑓(𝑥)|.
3. Для каких функций 𝑦 = 𝑓(𝑥) выполняется равенство 𝑓(𝑥) = |𝑓(𝑥)| для
всех 𝑥 ∈ 𝐷(𝑓)?
4. Постройте график функции.
a) 𝑦 = ||𝑥 + 1| − 1|
b) y = ||x 2 − x − 2| − 4|
5. Найти множество значений функции 𝑦 = |f(x)|, если известно
множество значений функции 𝑦 = f(x).
a) (−6; −2)
d) [−2; 5]
b) (−∞; 1]
e) (−6; −2) ∪ (1; 3)
c) (−∞; −2) ∪ (10; ∞)
f) (−5; −4) ∪ (1; 2]
6. Пусть функция 𝑦 = f(x) – периодическая с периодом 𝑇. Докажите, что
функция 𝑦 = |f(x)| тоже является периодической с периодом 𝑇.
Приведите пример, когда наименьший период функции 𝑦 = f(x) не
является наименьшим периодом функции 𝑦 = |f(x)|.
7. Будет ли обратимой функция 𝑦 = |f(x)|, если функция 𝑦 = f(x)
обратима?






