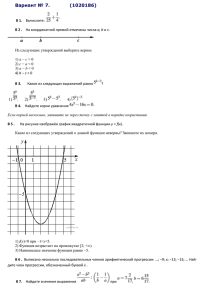
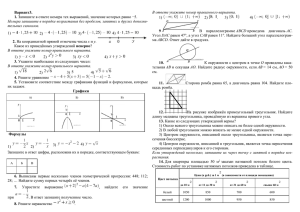
1. Найдите значение выражения 2. На координатной прямой

1. Найдите значение выражения
2. На координатной прямой отмечены числа a и b.
В ответе укажите номер правильного варианта.
Какое из следующих неравенств верно?
1)
2)
3)
4)
3. Какое из чисел больше:
или
В ответе укажите номер правильного варианта.
1)
2)
3)
4. Найдите наибольшее значение
, удовлетворяющее системе неравенств
5. Установите соответствие между графиками функций и формулами, которые их задают.
Формулы
1)
2)
3)
Графики
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
6. Даны пятнадцать чисел, первое из которых равно 6, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
7. Найдите значение выражения
8. Решите неравенство
при
,
и определите, на каком рисунке изображено множество его решений.
В ответе укажите номер правильного варианта.
9. У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
10.
Прямоугольный треугольник с катетами 5 см и 12 см вписан в
окружность. Чему равен радиус этой окружности?
11.
В треугольнике ABC отмечены середины M и Nсторон BC и AC соответственно. Площадь треугольника CNM равна 20. Найдите площадь четырёхугольника ABMN.
12.
Найдите тангенс угла
треугольника
13. Какие из следующих утверждений верны?
, изображённого на рисунке.
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого
треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то
площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
14. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая
из этих планет дальше всех от Солнца?
Планета
Марс
Меркурий Нептун
Сатурн
Расстояние (в км) 2,280 · 108 5,790 · 107 4,497 · 109 1,427 · 109
В ответе укажите номер правильного варианта.
1) Марс
2) Меркурий
3) Нептун
4) Сатурн
15. На рисунке изображён график изменения атмосферного давления в городе Энске за три
дня. По горизонтали указаны дни недели и время, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите значение атмосферного давления во вторник в 6
часов утра.
16.. Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько рублей
стоил товар до распродажи?
17. Мальчик прошёл от дома по направлению на восток 400 м. Затем повернул на север и
прошёл 90 м. На каком расстоянии (в метрах) от дома оказался мальчик?
18.
В магазине продаются футболки пяти размеров: XS,
S, M, L и XL. Данные по продажам в январе представлены на круговой диаграмме.
Какие утверждения относительно проданных в январе футболок неверны, если всего в январе
было продано 150 таких футболок?
1) Меньше всего было продано футболок размера XS.
2) Меньше половины проданных футболок – футболки размеров M и L.
3) Меньше половины всех проданных футболок – футболки размеров S и M.
4) Футболок размера XL было продано меньше 40 штук.
19. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4
группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
20. Площадь четырёхугольника можно вычислить по формуле
где d1 и d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой
формулой, найдите длину диагонали d2, если
а
21. Упростите выражение
22. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
23. Постройте график функции
и определите, при каких значениях
прямая
имеет с графиком ровно три общие точки.
24.
Найдите угол АСО, если его сторонаСА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°
25. В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL = AM. Докажите, что данный параллелограмм — прямоугольник.
26. В трапеции ABCD основания AD и BC равны соответственно 45 и 15, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и Bи касающейся
прямой CD, если AB = 9.