F ℓ

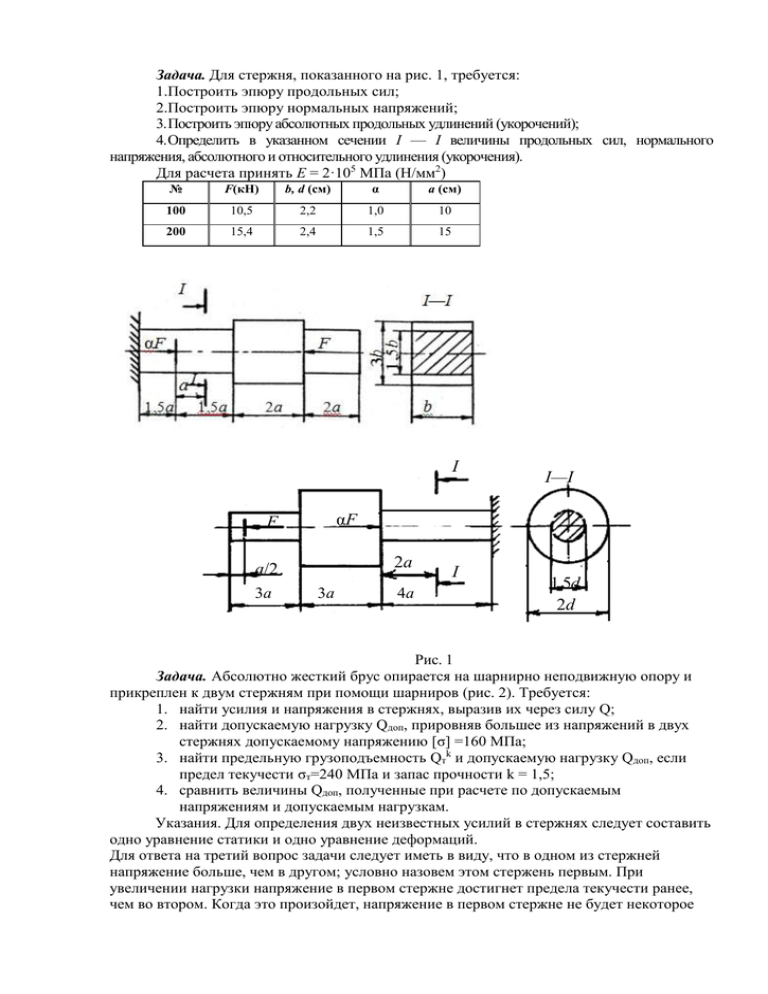
Задача. Для стержня, показанного на рис. 1, требуется:
1.Построить эпюру продольных сил;
2.Построить эпюру нормальных напряжений;
3. Построить эпюру абсолютных продольных удлинений (укорочений);
4. Определить в указанном сечении I — I величины продольных сил, нормального
напряжения, абсолютного и относительного удлинения (укорочения).
Для расчета принять Е = 2·105 МПа (Н/мм2)
№
F(кН)
b, d (см)
α
а (см)
100
10,5
2,2
1,0
10
200
15,4
2,4
1,5
15
I
αF
F
2а
а/2
3а
I—I
3а
4а
I
1,5d
2d
Рис. 1
Задача. Абсолютно жесткий брус опирается на шарнирно неподвижную опору и
прикреплен к двум стержням при помощи шарниров (рис. 2). Требуется:
1. найти усилия и напряжения в стержнях, выразив их через силу Q;
2. найти допускаемую нагрузку Qдоп, прировняв большее из напряжений в двух
стержнях допускаемому напряжению [σ] =160 МПа;
3. найти предельную грузоподъемность Qтk и допускаемую нагрузку Qдоп, если
предел текучести σт=240 МПа и запас прочности k = 1,5;
4. сравнить величины Qдоп, полученные при расчете по допускаемым
напряжениям и допускаемым нагрузкам.
Указания. Для определения двух неизвестных усилий в стержнях следует составить
одно уравнение статики и одно уравнение деформаций.
Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней
напряжение больше, чем в другом; условно назовем этом стержень первым. При
увеличении нагрузки напряжение в первом стержне достигнет предела текучести ранее,
чем во втором. Когда это произойдет, напряжение в первом стержне не будет некоторое
время расти даже при увеличении нагрузки, система станет как бы статически
определимой, нагруженной силой Q (пока еще неизвестной) и усилием в первом стержне:
N1= σтА1.
При дальнейшем увеличении нагрузки напряжение и во втором стержне достигнет
предела текучести:
N2= σтА2.
Написав уравнение статики и подставив в него значения усилий N1 и N2, находится
предельная грузоподъемность Qтk.
Рис.2
F(Н)
А(см2)
а (м)
b, (м)
с, (м)
110
11
2,2
2,2
1,1
200
20
2,0
2,0
2,0
Задача. Для заданного поперечного (рис. 3) сечения определить:
1. Координаты центра тяжести;
2. Осевые и центробежный моменты инерции сечения относительно центральных
осей;
3. Направление главных центральных осей инерции;
4. Величины главных центральных моментов инерции;
5. Главные центральные радиусы инерции сечения.
а, см
b, см
6
6
2
2
Рис.3
Задача. Для балки (рис. 4) необходимо:
1. Построить эпюры изгибающих моментов и поперечных сил;
2. Определить опасное сечение (по изгибу) и записать условие прочности;
3. Исходя из условия прочности подобрать: геометрические размеры
прямоугольного, (кольцевого, круглого сечений, и номера прокатной стали (профилей
двутавра, швеллера)); для расчета принять: предел текучести σт = 340 МПа (Н/мм), запас
прочности n = 2,1.
М
кНм
а
м
b
м
F
кН
q
кН/м
24
2
3
30
8
32
4
3
15
10
Рис. 4
Задача. На рис. 5 изображена в аксонометрии ось ломаного стержня круглого
поперечного сечения, расположенная в горизонтальной плоскости и имеющая прямые
углы в точках А и В. На стержень действует вертикальная нагрузка.
Требуется:
1.
построить отдельно (в аксонометрии) эпюры изгибающих и крутящих
моментов;
2.
установить опасное сечение и найти для него величину расчетного
момента по четвертой теории прочности.
В расчетах принять:допускаемое напряжение [σ] = 160 МПа
q
кН/м
l
м
d, см
α
8
2
5
1,0
10
4
6
2,0
Рис. 5
Задача. Для заданной статически неопределимой системы (рис. 6) требуется:
1. Раскрыть ее статическую неопределимость (методом сил, методом Верещагина или
методом Начальных параметров).
2. Построить окончательные эпюры изгибающих моментов (М), поперечных (Q) (и
продольных (N) сил, если рассчитывается рама).
3. Подобрать размеры круглого поперечного сечения.
Для расчета принять EJ = const; [σ] = 160 МПа
l (м)
h (м)
№
F (кН)
М (кНм)
q (кН/м)
1,6
2,8
10
10
22
5
F
q
ℓ/2
ℓ/4
ℓ/2
Рис.6
Задача. На стальную двутавровую балку, свободно лежащую на двух жестких опорах
с высоты h падает груз F (рис. 7). Требуется:
1. найти наибольшее нормальное напряжение в балке;
2. решить аналогичную задачу при условии, что правая опора заменена пружиной,
податливость которой (т. е. осадка от груза весом 1Н) равна α;
3. сравнить полученные результаты.
Исходные данные взять из табл. 8.
Указания. При наличии упомянутой в п. 2 пружины δст=δ+βδпр, где δ – прогиб
балки, лежащей на жестких опорах, в том сечении, где приложена сила F (при
статическом действии этой силы); δпр – осадка пружины от реакции, возникающей от силы
F; β – коэффициент, устанавливающий зависимость между осадкой пружины и
перемещением точки приложения силы F. Этот коэффициент вызван поворотом всей
балки вокруг центра шарнира левой опоры как жесткого целого и находится из подобия
треугольников
l (м)
h (см)
№
F кН)
α, мм2/Н
№
№ двутавра
2,1
11
10
1,1
21
1
20
Рис. 7