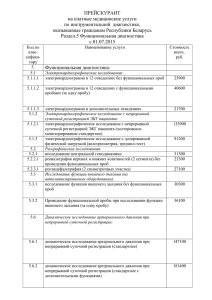
Передаточные функции импульсных фильтров

Передаточные функции импульсных
фильтров
На рис.8.5 представлена модель импульсного элемента ИЭ из рис.8.2.
Рис.8.5. Модель импульсного элемента
Задача идеального импульсного элемента (ИИЭ) в модели - сформировать для дальнейшего
математического описания системы либо последовательность импульсов типа σ-функций с
площадью f(t), либо решетчатую функцию, в основе которой единичная импульсная функция
σo(t) = { 1 при t равном 0; 0 при t не равном 0 } с амплитудой f(t).
Задача экстраполятора (Э) - математически описать выходную последовательность реального
импульсного звена (экстраполяция - это прогнозирование (синтез) сигнала между значениями
решетчатой функции).
Коэффициент передачи квантователя (ИИЭ) обратно пропорционален периоду квантования, а
коэффициент передачи экстраполятора нулевого порядка равен периоду. Таким образом,
общий коэффициент передачи квантующей и восстанавливающей цепи, т.е. ИЭ обычно равен
единице.
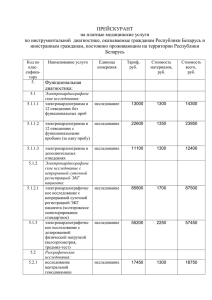
Если ИИЭ выдает решетчатую функцию, то можно ввести понятие "приведенной весовой
функции" - wп. Это реакция на единичный импульс, поданной на вход экстраполятора. Если
ИИЭ выдает последовательность типа σ-функций, то для непрерывной части совместно с
экстраполятором можно вывести понятие приведенной непрерывной передаточной функции:
Wп(р) = Wэ(р)Wнч(р), при этом Wп(р) = L{ wп(t) }.
Тогда для исследования импульсной системы ее структура приводится к расчетной схеме, как
показано на рис.8.6.
Рис.8.6. Расчетная функциональная схема разомкнутой импульсной системы
Идеальный импульсный элемент преобразует непрерывный сигнал в мгновенные импульсы в
виде σ-функций, модулированные по площади, а экстраполятор формирует импульсы заданной
формы из σ-функций, соответствующие форме выходного импульса реального импульсного
элемента. Реальные импульсы, проходя через линейную часть, вновь образуют непрерывный
сигнал y(p).
Пользуясь дискретным преобразованием Лапласа (8.4) можно найти дискретную приведенную
передаточную функцию экстраполятора и непрерывной части
(8.5)
Структурные преобразования импульсные систем несколько отличаются от структурных
преобразований линейных непрерывных САУ. В случае, когда приведенная непрерывная часть
состоит из параллельно включенных звеньев и на входе имеется общее импульсное звено, то
дискретная передаточная функция может быть определена суммированием дискретных
передаточных функции, определенных для каждого звена в отдельности.
. (8.6)
Если непрерывные звенья включены последовательно и имеется одно импульсное звено на
входе, то дискретная передаточная функция такого соединения
.
В этом случае дискретная передаточная функция W(z) должна определяться z преобразованием от произведения передаточных функций непрерывной части системы
W(z) = Z { W1(р) … Wi(p) }, те. W(z)
W1(z) … Wi(z) !!!
Нельзя переносить сумматор или любое непрерывное звено через импульсный элемент.
Непрерывную часть можно преобразовывать по известным правилам преобразования
структурных схем непрерывных САУ. Для схем, состоящих из импульсных фильтров, когда на
входе каждого непрерывного звена стоит свой импульсный элемент, справедливы все правила
преобразования структурных схем непрерывных систем. Для нахождения дискретных
передаточных функций можно пользоваться таблицами соответствий между функциями
времени, их изображениями по Лапласу и их z-изображениями [2,6].
Найдем дискретные передаточные функции для различных экстраполяторов. Для
экстраполятора нулевого порядка рис.8.1 изображение импульса
Тогда z - изображение экстраполятора и непрерывной части:
(8.7)
Если учесть наличие в непрерывной части звена чистого запаздывания е-рτ , то дискретная
передаточная функция в общем виде будет:
(8.8)
где ε - относительное смещение, отсчитываемое от начала предыдущего такта ε=1 - τ/T;
0<τ<T.
Для импульсной системы с экстраполятором, осуществляющим АИМ-первого или второго рода
(рис.8.1) изображение прямоугольного импульса единичной высоты и длительности γT можно
представить как
Тогда z - изображение экстраполятора и непрерывной части:
, где ε=1-γ (8.9)
Если импульсный элемент генерирует короткие по сравнению с периодом дискретности
прямоугольные импульсы, т.е. γ << 1, то можно приближенно принять е-γТp=1 - γTp. Тогда
получим
(8.10)
Формула (8.10) справедлива, если пренебречь влиянием конечной длительности импульса. В
большинстве случаев для выполнения этого достаточно, чтобы постоянные времени
непрерывной части системы были больше длительности импульса, т.е. Ti >> γТ (i = 1, 2, 3, ...).
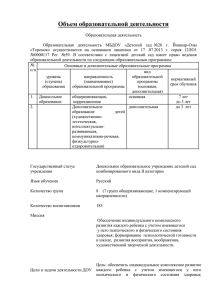
Пример задачи
Отметим некоторые особенности определения передаточных функций замкнутых импульсных
систем. На рис.8.7 приведена структурная схема замкнутой системы, которая содержит один
импульсный элемент ИЭ, одно управляющее воздействие g(t) и одно возмущающее f(t). При
этом f(t) приложено ко входу непрерывной части W2(p).
Рис. 8.7. Структурная схема замкнутой импульсной системы
Для получения передаточных функций замкнутых систем по управляющему и возмущающему
воздействиям а также по ошибкам от этих воздействий, целесообразно сначала привести
возмущающее воздействие ко входу импульсной системы, чтобы в дальнейшем исключить
ошибки определения z - преобразования от различных воздействий (рис.8.8).
Рис. 8.8. Приведенная структурная схема замкнутой импульсной системы
Тогда значения выходной величины Y(z) и ошибки Е(z) определятся выражениями:
- от возмущающего воздействия;
- от управляющего воздействия;
- от управляющего воздействия;
W(z)=Z {Wэ(р)W1(p)W2(p)} - z- изображение разомкнутой системы.