Нелинейные волны в двухжидкостной магнитной гидродинамике

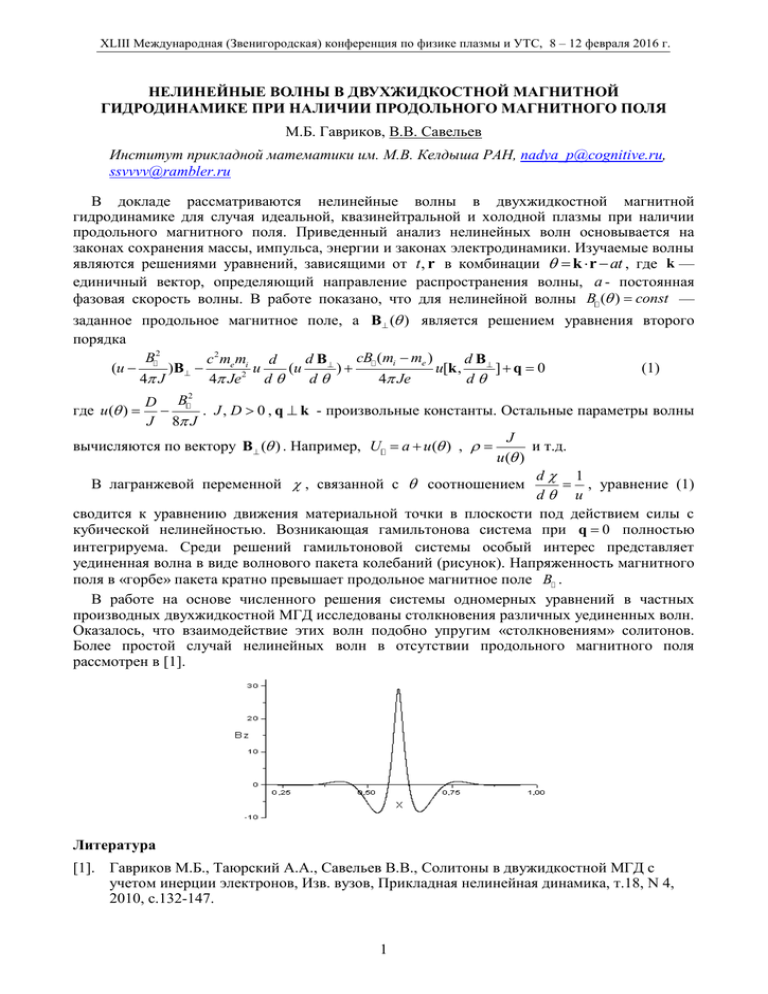
XLIII Международная (Звенигородская) конференция по физике плазмы и УТС, 8 – 12 февраля 2016 г.
НЕЛИНЕЙНЫЕ ВОЛНЫ В ДВУХЖИДКОСТНОЙ МАГНИТНОЙ
ГИДРОДИНАМИКЕ ПРИ НАЛИЧИИ ПРОДОЛЬНОГО МАГНИТНОГО ПОЛЯ
М.Б. Гавриков, В.В. Савельев
Институт прикладной математики им. М.В. Келдыша РАН, nadya_p@cognitive.ru,
ssvvvv@rambler.ru
В докладе рассматриваются нелинейные волны в двухжидкостной магнитной
гидродинамике для случая идеальной, квазинейтральной и холодной плазмы при наличии
продольного магнитного поля. Приведенный анализ нелинейных волн основывается на
законах сохранения массы, импульса, энергии и законах электродинамики. Изучаемые волны
являются решениями уравнений, зависящими от t , r в комбинации   k  r  at , где k —
единичный вектор, определяющий направление распространения волны, a - постоянная
фазовая скорость волны. В работе показано, что для нелинейной волны B ( )  const —
заданное продольное магнитное поле, а B  ( ) является решением уравнения второго
порядка
B2
cB (mi  me )
c 2 me mi d
d B
d B
(u 
)B  
u
(u
)
u[k ,
]q  0
(1)
2
4 J
4 Je
d
d
4 Je
d
2
D B

. J , D  0 , q  k - произвольные константы. Остальные параметры волны
J 8 J
J
вычисляются по вектору B  ( ) . Например, U  a  u ( ) ,  
и т.д.
u ( )
d 1
В лагранжевой переменной  , связанной с  соотношением
 , уравнение (1)
d u
сводится к уравнению движения материальной точки в плоскости под действием силы с
кубической нелинейностью. Возникающая гамильтонова система при q  0 полностью
интегрируема. Среди решений гамильтоновой системы особый интерес представляет
уединенная волна в виде волнового пакета колебаний (рисунок). Напряженность магнитного
поля в «горбе» пакета кратно превышает продольное магнитное поле B .
В работе на основе численного решения системы одномерных уравнений в частных
производных двухжидкостной МГД исследованы столкновения различных уединенных волн.
Оказалось, что взаимодействие этих волн подобно упругим «столкновениям» солитонов.
Более простой случай нелинейных волн в отсутствии продольного магнитного поля
рассмотрен в [1].
где u ( ) 
Литература
[1]. Гавриков М.Б., Таюрский А.А., Савельев В.В., Солитоны в двужидкостной МГД с
учетом инерции электронов, Изв. вузов, Прикладная нелинейная динамика, т.18, N 4,
2010, с.132-147.
1