Конференция_Нгуен_Чи_Тхань_Ньан

ВЫЧИСЛЕНИЕ ОПТИЧЕСКОГО ПОТОКА МЕТОДОМ
ЛУКАСА – КАНАДЕ
Нгуен Чи Тхань Ньан,
Национальный исследовательский Томский политехнический университет, г. Томск
Научный руководитель – Аметова Эвелина Серверовна
1.
Введение
Задачи автоматического выделения и отслеживания объектов по признаку их движения
на изображениях, получаемых от различных видео датчиков, часто возникают при разработке
систем видеонаблюдения и систем машинного зрения, предназначенных для мобильных
технических средств. На основе последовательности кадров, изображающих трехмерное
пространство, необходимо построить изменения, которые происходят с ним с течением
времени.
Оптический поток
Оптический поток– это отображение видимого движения, представляющее собой
смещение каждой точки между двумя изображениями.По сути, оптический поток –
представляет собой поле скоростей, так каксдвиг точки между двумя изображениями
эквивалентен мгновенной скорости.
В теории вычисления оптического потока используются следующие определения:
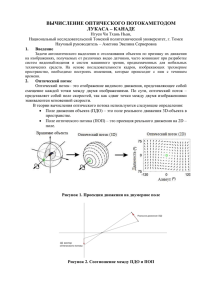
 Поле движения объекта (ПДО) – это поле реального движения 3D-объекта в
пространстве.
 Поле оптического потока (ПОП) – это проекция реального движения на 2D –
поле.
2.
Рисунок 1. Проекция движения на двумерное поле
Рисунок 2. Соотношение между ПДО и ПОП
Пусть 𝐼(𝑥, 𝑦, 𝑡)–интенсивность точки в пикселе(𝑥, 𝑦)в момент𝑡на первом кадре.
Тогда через интервал времени 𝛿𝑡,точка в пикселе (x,y) будет перемещена на𝛿𝑥 и 𝛿𝑦на
втором кадре. Допустим, что интенсивность точки не изменяется, тогда:
𝐼(𝑥, 𝑦, 𝑡) = 𝐼(𝑥 + 𝛿𝑥, 𝑦 + 𝛿𝑦, 𝑡 + 𝛿𝑡)
(1)
Разложим (1) в ряд Тейлора:
𝜕𝐼
𝜕𝐼
𝜕𝐼
𝐼 (𝑥 + 𝛿𝑥, 𝑦 + 𝛿𝑦, 𝑡 + 𝛿𝑡) ≈ 𝐼 (𝑥, 𝑦, 𝑡) + 𝜕𝑥 𝛿𝑥 + 𝜕𝑦 𝛿𝑦 + 𝜕𝑡 𝛿𝑡 + 𝐻. 𝑂. 𝑇
(2)
Из (1)и (2):
𝜕𝐼 𝛿𝑥
𝜕𝑥 𝛿𝑡
𝜕𝐼 𝛿𝑦
𝜕𝐼 𝛿𝑡
+ 𝜕𝑦 𝛿𝑡 + 𝜕𝑡 𝛿𝑡 = 0
Следовательно,
𝐼𝑥 𝑣𝑥 + 𝐼𝑦 𝑣𝑦 + 𝐼𝑡 = 0
где𝑣𝑥 , 𝑣𝑦 —Скорости оптического потока в точке (𝑥, 𝑦).
𝜕𝐼
𝜕𝐼
𝜕𝐼
𝐼𝑥 = 𝜕𝑥 , 𝐼𝑦 = 𝜕𝑦 , 𝐼𝑡 = 𝜕𝑡—частные
производные
по
пространственным
координатам и времени.
Таким образом,
𝛻𝐼 𝑇 ⋅ 𝑣⃗ = −𝐼𝑡
(3)
Уравнение (3)– этоуравнение оптического потока. Данное уравнение содержит
две неизвестные переменные 𝑣𝑥 , 𝑣𝑦 . Следовательно,система уравнений недоопределенная. Вычисление оптического потока – нахождение векторов𝑣⃗(𝑣𝑥 , 𝑣𝑦 )для
оценки движения объекта.
3.
Метод Лукаса–Канаде
Алгоритм Лукаса – Канаде– один из методов, применяющихсядля вычисления
оптического потока. Данный алгоритм используется достаточношироко в задачах
оценки движения объекта.Алгоритм Лукаса-Канадеявляется локальным методом
вычисления оптического потока, так как обрабатывает пиксели в окрестности
определенной точки.
Данный алгоритм предполагает, что:
a) Смещение точек на двух изображении незначительное.
b) Смещение точек в окрестностинекоторой точки 𝑝одинаково.
Допустим, чтоD={𝑞1 , 𝑞2 , … , 𝑞𝑛 } –набор точек в окрестности точки 𝑝(𝑥, 𝑦). Тогда,
получаем систему уравнений
𝐼𝑥 (𝑞1 )𝑣𝑥 + 𝐼𝑦 (𝑞1 )𝑣𝑦 = −𝐼𝑡 (𝑞1 )
𝐼𝑥 (𝑞2 )𝑣𝑥 + 𝐼𝑦 (𝑞2 )𝑣𝑦 = −𝐼𝑡 (𝑞2 )
(4)
…
{𝐼𝑥 (𝑞𝑛 )𝑣𝑥 + 𝐼𝑦 (𝑞𝑛 )𝑣𝑦 = −𝐼𝑡 (𝑞𝑛 )
Обычно набор точек в окрестности точки 𝑝ограничен окном𝑁 × 𝑀cцентром 𝑝.
Проблема включается в том, что чем больше количества точек в
окрестноститочки 𝑝, тем больше уравнений будет содержать система(4) для
нахождения вектора 𝑣⃗.Например, для окна 3 × 3потребуется решить систему из 9
уравнений.
Для решения данной проблемы применяетсявзвешенный метод наименьших
квадратов.Для определения весовых коэффициентов для пикселей на изображении
используется функция 𝑊(𝑥, 𝑦). Согласно взвешенному методу наименьших квадратов,
для нахождения решения необходимо минимизировать невязку:
𝜖(𝑣) = ∑ 𝑊(𝑥, 𝑦)[𝐼(𝑥, 𝑦, 𝑡) − 𝐼(𝑥 + 𝛿𝑥, 𝑦 + 𝛿𝑦, 𝑡 + 𝛿𝑡)]2
𝑥,𝑦∈𝐷
𝜕𝐼
𝜕𝐼
𝜕𝐼
= ∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦)(𝜕𝑥 𝑣𝑥 + 𝜕𝑦 𝑣𝑦 + 𝜕𝑡)2
где 𝑣 = (𝑣𝑥 , 𝑣𝑦 )
Тогда,
𝜕𝜖(𝑣)
𝜕𝐼
𝜕𝐼
𝜕𝐼 𝜕𝐼
= 2 ∑ 𝑊(𝑥, 𝑦) ( 𝑣𝑥 +
𝑣𝑦 + )
𝑑𝑣𝑥
𝜕𝑥
𝜕𝑦
𝜕𝑡 𝜕𝑥
𝑥,𝑦∈𝐷
𝜕𝐼 2
𝜕𝐼 𝜕𝐼
𝜕𝐼 𝜕𝐼
= 2 ∑ 𝑊(𝑥, 𝑦)[( ) 𝑣𝑥 +
𝑣𝑦 +
]
𝜕𝑥
𝜕𝑦 𝜕𝑥
𝜕𝑡 𝜕𝑥
𝑥,𝑦∈𝐷
𝜕𝜖(𝑣)
𝜕𝐼
𝜕𝐼
𝜕𝐼 𝜕𝐼
= 2 ∑ 𝑊(𝑥, 𝑦) ( 𝑣𝑥 +
𝑣𝑦 + )
𝑑𝑣𝑦
𝜕𝑥
𝜕𝑦
𝜕𝑡 𝜕𝑦
𝑥,𝑦∈𝐷
𝜕𝐼 𝜕𝐼
𝜕𝐼 2
𝜕𝐼 𝜕𝐼
= 2 ∑ 𝑊(𝑥, 𝑦)[
𝑣𝑥 + ( ) 𝑣𝑦 +
]
𝜕𝑥 𝜕𝑦
𝜕𝑦
𝜕𝑡 𝜕𝑦
𝑥,𝑦∈𝐷
Для нахождения минимума ошибки 𝜖(𝑣)необходимо приравнять
𝜕𝜖(𝑣) 𝜕𝜖(𝑣)
𝑑𝑣𝑥
,
𝑑𝑣𝑦
Следовательно, получаем:
𝜕𝐼 2
𝜕𝐼 𝜕𝐼
𝜕𝐼 𝜕𝐼
∑ 𝑊(𝑥, 𝑦)[( ) 𝑣𝑥 +
𝑣𝑦 +
]=0
𝜕𝑥
𝜕𝑦 𝜕𝑥
𝜕𝑡 𝜕𝑥
нулю.
(5)
𝑥,𝑦∈𝐷
𝜕𝐼 𝜕𝐼
𝜕𝐼 2
𝜕𝐼 𝜕𝐼
∑ 𝑊(𝑥, 𝑦)[
𝑣𝑥 + ( ) 𝑣𝑦 +
]=0
𝜕𝑥 𝜕𝑦
𝜕𝑦
𝜕𝑡 𝜕𝑦
(6)
{𝑥,𝑦∈𝐷
Уравнения (5) и (6) могут быть представлены в матричной форме:
𝜕𝐼 2
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦) ( )
𝜕𝑥
[
𝜕𝐼
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦)(
𝜕𝐼
𝜕𝑥 𝜕𝑦
)
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦)(
𝜕𝐼 𝜕𝐼
)
𝑣𝑥
𝜕𝑦 𝜕𝑥
] [𝑣 ]
2
𝑦
𝜕𝐼
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦) ( )
𝜕𝑦
+[
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦)(
𝜕𝐼 𝜕𝐼
𝜕𝑡 𝜕𝑥
𝜕𝐼 𝜕𝐼
∑𝑥,𝑦∈𝐷 𝑊(𝑥, 𝑦)(
)
)
𝜕𝑡 𝜕𝑡
]=0
Пусть:
𝜕𝐼 2
∑ 𝑊(𝑥, 𝑦) ( )
𝜕𝑥
𝐴=
𝑥,𝑦∈𝐷
𝜕𝐼 𝜕𝐼
∑ 𝑊(𝑥, 𝑦) (
)
𝜕𝑥 𝜕𝑦
[𝑥,𝑦∈𝐷
Тогда,
𝜕𝐼 𝜕𝐼
∑ 𝑊(𝑥, 𝑦) (
)
𝜕𝑦 𝜕𝑥
𝑥,𝑦∈𝐷
2
𝜕𝐼
∑ 𝑊(𝑥, 𝑦) ( )
𝜕𝑦
𝑥,𝑦∈𝐷
∑ 𝑊(𝑥, 𝑦) (
𝑣𝑥
, 𝑣 = [𝑣 ] , 𝐵 =
𝑦
]
𝑥,𝑦∈𝐷
𝜕𝐼 𝜕𝐼
)
𝜕𝑡 𝜕𝑥
𝜕𝐼 𝜕𝐼
∑ 𝑊(𝑥, 𝑦) (
)
𝜕𝑡 𝜕𝑡
[ 𝑥,𝑦∈𝐷
]
𝐴. 𝑣 + 𝐵 = 0
⟺ 𝑣 = −𝐴−1 𝐵
Вычисление оптического потока в MatLab.
Для вычисления оптического тока методом Лукаса-Канаде воспользуемся
библиотекой MatLab «Computer vision system toolbox». Вычислим оптический поток для
двух изображений, представленных на рисунке 3.
Результат вычисления оптического потока показан на рисунке 4. В полученном
изображении черные пиксели соответствуют неподвижной части изображения, а белые
– движущейся.
4.
Рисунок 3. Входные изображения
Рисунок 4 - Результат расчета оптического потока
Заключение
В данной работе были рассмотрены понятие оптического потока и основыметода
Лукаса-Канадедля вычисленияоптического потока. В качестве примера было
рассмотрено вычислениеоптического потока в MatLab.
Данный алгоритм является достаточно простым и быстрым. Во многих случаях
метод Лукаса-Канадедостаточно эффективен. Среди недостатков алгоритма следует
отметить, что данный метод эффективен только при небольших смещениях объекта
между кадрами.
Для решения указанных проблем на практике используется комбинация метода
Лукаса – Канаде с другими методами, например, с методом определения угла объекта и
методом пирамиды.
5.
Список использованных источников
1. Lucas B. and Kanade. T. An iterative image registration technique with an application
to stereo vision. Proc. DARPA IU Workshop,с. 121–130. 1981.
2. Barron J. L., Fleet D. J., and Beauchemin S. S. Performance of optical flow
techniques. International Journal of Computer Vision, 12(1),с. 43–77. 1994
3. Alireza Bab–Hadiashar, David Suter. Robust Optic Flow Computation. - International
Journal of Computer Vision 29(1), с. 59–77. 1998
4. Вишняков Б.В., Визильтер Ю.В., Лагутенков А.В. Использование
модифицированного метода оптических потоков в задаче обнаружения и
межкадрового прослеживания движущихся объектов. ФГУП ГосНИИ
Авиационных Систем, 2004. – 12 с.
5. Шалабанов А.К., Роганов Д.А.Эконометрика [Электронный ресурс]: учебное
пособие / Шалабанов А.К., Роганов Д.А.;Университет управления «ТИСБИ». Казань: Издательство ТИСБИ, 2004. – 203с.
6. Вычисление оптического потока методом Лукаса-Канаде. Теория // habrahabr.ru.
[2013-1014]. Дата обновления: 18.02.2013.
URL: http://habrahabr.ru/post/169055/(дата обращения: 31.03.2014).
7. Lucas-Kanadealgorithm. // Copterix. [2011 – 2014].
URL: http://copterix.perso.rezel.net/?page_id=58 (дата обращения: 31.03.2014).
8. Обобщенныйметоднаименьшихквадратов. //Википедия. [2013-2014].
URL:http://ru.wikipedia.org/wiki/Обобщенный_метод_наименьших_квадратов
(дата обращения: 31.03.2014).
9. Оптический поток // Википедия. [2013 – 2014]. Дата обновления: 04.03.2014.
URL: http://ru.wikipedia.org/Оптический_поток (дата обращения: 31.03.2014).