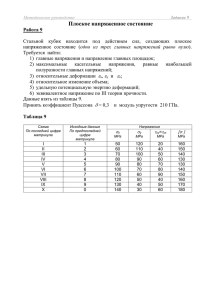
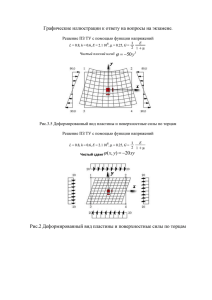
Напряженно – деформированное состояние в точке упругого тела

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
КАФЕДРА «ОБЩЕТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ»
ИССЛЕДОВАНИЕ ПЛОСКОГО
НАПРЯЖЕННОГО СОСТОЯНИЯ
Методические указания
к практическим занятиям по дисциплине
«Сопротивление материалов»
РПК «Политехник»
Волгоград
2005
УДК 539.3/.6(07)
И 88
ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ:
Методические указания к практическим занятиям по дисциплине «Сопротивление материалов» / Сост. С. Г. Корзун, А. В. Белов, Н. Г. Неумоина; Волгоград. гос. техн. ун-т. – Волгоград, 2005. – 14 с.
Рассматриваются методы определения напряжений при плоском
напряженном состоянии, предлагаются индивидуальные задания, приводится пример выполнения.
Ил. 12. Табл. 1. Библиогр.: 3 назв.
Рецензент Е. А. Малявин
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
©
2
Волгоградский
государственный
технический
университет, 2005
ОСНОВЫ ТЕОРИИ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО
СОСТОЯНИЕ В ТОЧКЕ УПРУГОГО ТЕЛА
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4
Тема: исследование плоского напряженного состояния.
Цель занятия: Освоить методику определения напряжений при
плоском напряженном состоянии.
Время отведенное на проведения занятия и выполнения индивидуального задания: 4 часа, в том числе 2 часа аудиторных занятий и 2
часа самостоятельной работы студентов
1.




ПОРЯДОК ПРОВЕДЕНИЯ ЗАНЯТИЯ
повторить теоретический материал;
ответить на контрольные вопросы;
разобрать приведенный пример решения задачи;
решить самостоятельно предложенное индивидуальное задание.
2. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
Для оценки прочности элементов конструкций, деталей машин
необходимо уметь определять величину наибольшего напряжения, возникающего в материале под нагрузкой и положение сечения в котором
оно действует, то есть величина напряжения связана непосредственно с
определённой частицей материала (точкой) и определённым сечением.
Для решения таких вопросов необходимо уметь анализировать
напряженное состояние в точке упругого тела.
Напряженным состоянием в точке упругого тела называется совокупность напряжений, действующих по всевозможным площадкам, проходящим через данную точку.
Площадки, в которых отсутствуют касательные напряжения, называются главными площадками.
Нормальные напряжения, действующие в главных площадках, называются главными напряжениями.
Через каждую точку тела можно провести как минимум три главных
площадки.
3
Наибольшее (в алгебраическом смысле) главное напряжение обозначают σ1, наименьшее σ3, а промежуточное σ2; таким образом, σ1 > σ2 > σ3.
Различают три вида напряженного состояния в зависимости от наличия или отсутствия главных напряжений:
Линейное (одноосное) – случай напряженного состояния, при котором два главных напряжения равны нулю (рис. 1 а).
Плоское – такой случай напряженного состояния, при котором одно
из трех главных напряжений равны нулю (рис. 1 б).
2
1
1
2
1
2
3
1
2
а
б
в
Рис. 1
Объемное – такой случай напряженного состояния, при котором все
три главных напряжения отличны от нуля (рис. 1 в).
Наибольший практический интерес представляет собой плоское
напряженное состояние. При этом имеет место два типа задач: прямая и
обратная.
2.1. Прямая задача
Известны главные напряжения σ1
и σ2 (рис. 2).
Требуется определить величину
нормальных и касательных напряжений в площадке, расположенной под
углом α к главной площадке с
наибольшим главным напряжением.
Аналитическое
решение
осуществляется по формулам:
σα = σ1·соs2α + σ2·sin2α
(1)
1   2
(2)
 
 sin 2
2
n
1
2
2
1
Рис. 2
4
При использовании формул (1) и (2) для входящих в них величин
применяют следующие правила знаков:
1) для угла α: положительный угол между направлением нормали
к произвольной площадке и направлением σ1 отсчитывается против часовой стрелки (рис. 3).
1
1
Рис. 3
2) для : нормальное напряжение считается положительным, если
вектор напряжения направлен в сторону внешней нормали (от сечения),
что соответствует растяжению элемента (рис. 4).
n
n
Рис. 4
3) для : касательное напряжение считается положительным, если
внешнюю нормаль к площадке для совмещения с направлением касательного напряжения необходимо повернуть по часовой стрелке.
Возможна и иная формулировка этого правила: касательное напряжение
считается положительным, если его вектор стремиться повернуть элемент вокруг точки, взятой внутри элемента по часовой стрелке (рис. 5 а) и отрицательным – если против часовой стрелки (рис. 5 б).
n
n
а
б
Рис. 5
При решении задач необходимо использовать свойства напряжений,
действующих по двум взаимно перпендикулярным площадкам, проходящим через одну и ту же точку.
5
1. Сумма нормальных напряжений, действующих по любым двум
взаимно перпендикулярным площадкам, проходящим через одну и ту же
точку, есть величина постоянная.
 +  = max + min = const.
2. Касательные напряжения в двух взаимно перпендикулярных
площадках равны по абсолютной величине и противоположны по знаку.
 = -.
Это утверждение называется законом парности касательных напряжений.
ta
tb
ta
90
90
tb
Рис. 6
Графическое решение прямой задачи осуществляется в результате
построения круговой диаграммы напряжений (круга Мора). Круг Мора –
это геометрическое место точек, абсциссы и ординаты которых равны
соответствующим нормальным и касательным напряжениям, возникающим на соответствующих наклонных площадках (площадках данной серии).
Семейством или серией площадок называют совокупность бесчисленного множества площадок, параллельных одной и той же прямой
(перпендикулярных одной и той же грани элементарного параллелепипеда), и проходящих через одну и ту же точку.
Подробное описание графического способа решения прямой задачи
[(1) с. 101-102].
Чаще на практике встречается обратная задача плоского напряжённого состояния.
2.2. Обратная задача
Даны нормальные и касательные напряжения, действующие в двух
взаимноперпендикулярных площадках: , , , . Требуется определить положение главных площадок и значения главных напряжений.
а) Определение напряжений в произвольной площадке, расположенной под углом , к площадке с наибольшим нормальным напряжением.
Пусть   ,   0 (см. рис. 7).
Аналитическое решение:
 = σα  cos2 + σβ  sin2 - ταsin2;
(3)
6
 
sj
j
sa
tj
j <
0 0
tb
ta
(4)
sb
smin
45
sa
 sin 2     cos 2 .
sb
tb
ta
 
2
ta
ta
t max
sa
sa
t min
tb
tb
sb
sb
Рис. 7
smax
Рис.8
б) Определение величины главных напряжений осуществляется по
формуле:
    1
(5)
 max,min 

     2  4 2 ,
2
2
где ,  – нормальные напряжения, действующие в 2-х взаимно
перпендикулярных площадках, перпендикулярных главной площадке, в
которой  = 0 и проходят через одну и ту же точку.
Положение главной площадки определяют с помощью формулы:
2r
.
(6)
tg20 
   


Для получения направления нормали к главной площадке угол φ0 откладывают от нормали к площадке с алгебраически большим по величине напряжением против часовой стрелки если φ0  0, и по часовой – если φ0  0.
Для данного случая φ0  0, что следует из формулы (6), так как   0,
а   .
Проверить правильность аналитического решения с построением
главных площадок можно следующим образом.
Для определения положения главной площадки с напряжением max
площадку с большим (в алгебраическом смысле) нормальным напряжением следует повернуть на угол φ0 в направлении, в котором вектор каса7
тельного напряжения, действующего по этой площадке, стремится вращать элементарный параллелепипед (элемент) относительно его центра.
в) определение величины экстремальных касательных напряжений:

  min
1
(7)
 max,min  max

   2  4 2 .
2
2
Эти напряжения имеют место в сечениях, наклоненных под углом
45 к главным площадкам, в которых действуют max и min.
Следует отметить, что нормальные напряжения, действующие в
площадках с экстремальными касательными напряжениями, не представляют практического интереса и потому на схеме не показаны.


3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ И ПРИМЕР
ИССЛЕДОВАНИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ
3.1. Индивидуальные задания
1. Определить аналитически
и графически величину и направление главных напряжений и показать
их на элементе.
2. Определить аналитически
и графически σ и τ на площадке,
нормаль к которой расположена
под углом φ к напряжению .
3. Определить
графически
направление площадок, на которых
действуют экстремальные касательные напряжения.
Исходные данные приведены
на рис. 9 и в таблице.
Рис. 9
Таблица
№
п/п
1
2
3
4
5
6
7
8

мПа
40
30
-20
-10
-40
50
-40
0

мПа
20
50
30
-20
-20
0
0
60

мПа
10
-20
20
10
-40
20
20
30
8

30
-30
45
-45
60
-60
120
-120

мПа
40
20
-15
-15
-2
5
-20
-5

мПа
9,8
10,3
-25
11
30
25
-28,5
24,1
Продолжение таблицы
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0
0
-40
-10
50
-40
-60
10
20
-30
40
-20
10
30
-30
30
30
15
-35
-25
45
-50
-80
0
20
-20
50
-40
40
-10
-30
-50
20
50
10
-40
-30
20
-40
-45
15
-45
15
-30
25
25
-30
-10
10
-20
0
-10
-20
20
40
-20
50
30
40
10
25
35
20
10
-35
-20
135
-135
150
-150
30
-30
45
-45
60
-60
120
-120
135
-135
150
-150
30
-30
45
-45
60
-60
-10
15
25
-15
45
-30
-20
11,5
25
-40
50
15
-25
29,9
-50
20
25,8
-30
10
-25
0
-20
-30,2
-20
24,1
-11
-8,7
17,3
-4,9
8
-25
-22,5
35,8
-37,6
35,7
30
-34,6
9,8
30
-31,6
25
-9,8
23,3
4,2
3.2. Пример
Для заданного напряженного состояния аналитически и графически
определить: величину и направление главных напряжений; величину нормального и касательного напряжений
sb
на площадке, нормаль к которой расtb
положена под углом  к направлению
. А также графически определить
направление площадок, на которых
ta
sa
sa действуют экстремальные касательj
ные напряжения.
ta
Дано:  = 20 МПа;
 = 50 МПа;
 = - 10 МПа;
 = 30.
tb
sb
Рис. 10
9
3.2.1. Аналитическое решение
1. Составим схему напряженного состояния с учетом принятых
правил знаков (рис. 10).
2. Определяем величину главных напряжений по формуле (5):
20  50 1
20  50 2  4   10 2 
 max,min 

2
2
1
30 2  400  35  12 1300 
 35 
2
1
 35  36  35  18 (МПа );
2
σmax = 1 = 35 + 18 = 53 МПа; σmin= 2 = 35 - 18 = 17 МПа, 3 = 0.
3. Определяем направления главных площадок по формуле (6):
2   10   20
tg20 

 0,6667 ;
50  20
30
2φ0 = -3342/ φ0 = -1651/.
Угол 0 откладываем от направления большего напряжения  по
часовой стрелке и получаем направление max, т.к. φ0  0.
Иными словами, чтобы получить элемент, ограниченный главными
площадками необходимо повернуть заданный элемент в направление часовой стрелки на угол φ0 = 1651/.
4. Определяем нормальные напряжения на площадке  по формуле (3):
2
2
 3
  50  1    10  3 
   20 
 2 
2
2


3
1
 20   50  10  0,866  15  12 ,5  8,66  36 ,16 МПа .
4
4
5. Определяем касательные напряжения на площадке  по формуле (4):
20  50
 
sin 60   (10 )  cos 60  
2
 15  0,866  10  0,5  12,99  5  17 ,99 МПа .
3.2.2. Графическое решение
Строим круг напряжений в следующем порядке (рис. 11):
1. Проводим оси координат -.
2. Выбираем масштаб: 1 см = 5 МПа, т. е. , = 5 МПа/см.
3. Строим точку D с координатами , , D (, ).
4. Строим точку D (, ).
5. Соединяем полученные точки отрезком прямой, точка С пересечения которого с осью  есть центр круга напряжений.
10
6. Радиусом СDα или CDβ проводим окружность.
7. Фиксируем точки А и В, точки пересечения окружности с осью σ.
8. Отрезок ОА в выбранном масштабе есть величина σmax, а отрезок ОВ - σmin.
9. Для определения направления главных площадок найдем полюс, для чего через точки Dα и Dβ проведем направления соответствующих площадок α и ß, точка Р пересечения которых есть полюс.
10. Соединив полюс с точкой А, получим направление главной
площадки, где действуют σmax.
11. Соединив полюс с точкой В, получим направление главной
площадки с σmin.
12. Направления главных напряжений совпадают с направлением
внешней нормали к площадке, если главные напряжения положительны и
внутренней – если отрицательны.
13. Для определения напряжений σ и τ необходимо из полюса Р
провести прямую, параллельную этой площадке до пересечения с окружностью (кругом Мора) в точке D, абсцисса которой равна (в принятом
масштабе) нормальному напряжению σ,, а ордината – касательному τ в
заданной площадке.
t, МПа
tmax
30
20
0
-10
-20
-30
Db
Р
10
10 В
snin
20
30 С
Da
50 A
40
s, МПа
smax
Dj
tmin
tj s
j
Рис. 11
Изобразим схему напряженного состояния с указанием напряжений
величина которых была определена в данном примере (рис. 12).
11
j0
sb
tb
s max
j
0
tj
sa
sj j
ta
sa
ta
tb
smin
sb
Рис. 12
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется напряженным состоянием в точке упругого тела?
2. Что такое главные площадки и главные напряжения? Как соотносятся величины главных напряжений?
3. Сколько главных площадок можно провести через одну и ту же
точку упругого тела?
4. Виды напряженного состояния.
5. Правила знаков для нормальных и касательных напряжений и
для угла .
6. Формулы для определения величины главных напряжений и для
определения положения главных площадок.
7. Формулы для определения экстремальных касательных напряжений. Как расположены площадки, в которых они действуют по отношению к главным площадкам?
8. Свойства нормальных и касательных напряжений действующих
на двух взаимно перпендикулярных площадках.
9. Порядок построения круга Мора.
10. Как определить полюс круга Мора?
11. Как определить направление главных площадок с помощью
круга Мора?
12. Как определить главные напряжения с помощью круга Мора?
12
13. Как определить с помощью круга Мора  и  в произвольной
площадке?
14. Как определить с помощью круга Мора экстремальные касательные напряжения и положение площадок, в которых они действуют?
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Дарков А. Е., Шпиро Г. С. Сопротивление материалов. Учебник
для технических вузов – 5-е изд., перераб. и доп. – М.: Высш. шк. 1989 –
624 с: ил.
2. Феодосьев В. И. Сопротивление материалов. – М.: Наука, 1986 –
512 с.
3. Костенко Н. А. Сопротивление материалов – М.: Высш. шк.
2000 – 430c: ил.
13
Составители: Светлана Григорьевна Корзун
Александр Владимирович Белов
Наталья Георгиевна Неумоина
ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ
Методические указания к практическим занятиям по дисциплине
«Сопротивление материалов»
Под редакцией авторов
Темплан 2005 г., поз. № 59.
Подписано в печать 3. 11. 2005 г. Формат 60×84 1/16.
Бумага потребительская. Гарнитура ”Times“.
Усл. печ. л. 0,88. Усл. авт. л. 0,69.
Тираж 100 экз. Заказ
Волгоградский государственный технический университет
400131 Волгоград, просп. им. В. И. Ленина, 28.
РПК «Политехник»
Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35.
14