Графические иллюстрации к экзамену 2015x
реклама
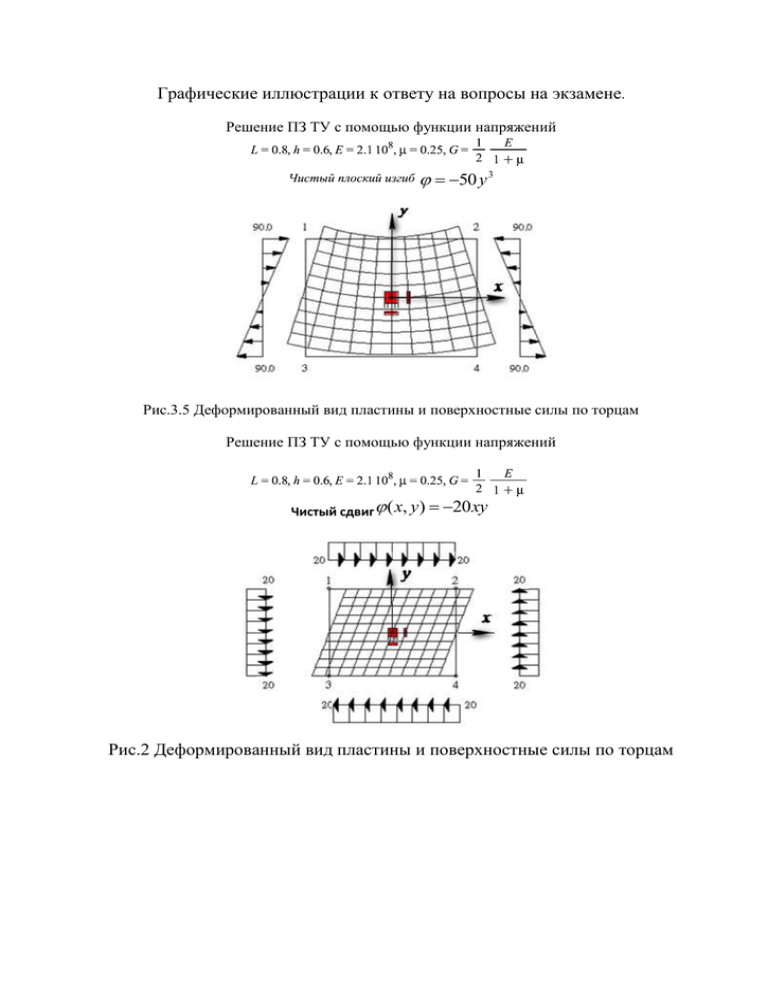
Графические иллюстрации к ответу на вопросы на экзамене. Решение ПЗ ТУ с помощью функции напряжений 50 y 3 Рис.3.5 Деформированный вид пластины и поверхностные силы по торцам Решение ПЗ ТУ с помощью функции напряжений Чистый сдвиг ( x, y ) 20 xy Рис.2 Деформированный вид пластины и поверхностные силы по торцам Расчет балки – стенки (задача Файлона) Исходных данные: L=120 см, h=30 см, δ=1 см, a= 2 см (L, h>> δ). Интенсивность равномерно распределенной нагрузки на участке малой площади по верхней кромке равна qB=500 МПа, а интенсивности опорных реакций qH=250 МПа. Для сравнения результатов расчета балки-полосы с расчетами по обычной балочной теории укажем величины сосредоточенной силы и опорных реакций. Распределенные нагрузки на малой площади a* δ=2 см2, соответствуют действию на балку-полосу сосредоточенной силы F=100 кН и опорных реакций Ra=Rb= 50кН. Рис.4.1 Балка-полоса Рис. 4.3 Поверхность напряжений σx Рис.4.4 Эпюры напряжений σx Рис. 4.4а ПЗТУ. Сечение х=58см. Напряжения σx Рис.4.5 Напряжения σy Рис.4.7 Напряжения τxy Рис. 4.4б ПЗТУ и балочная теория. Сечение х=58см. Напряжения σx Рис.4.6 Эпюры напряжений σy Рис. 4.8 Эпюры напряжений τxy Рис. 4.8а Эпюры касательных напряжений Рис.4.9 Напряжения m ax Рис. 4.8б Эпюры напряжений (х=58см) Рис.4.10 Напряжения m in Рис.4.11 Картина напряженного состояния Рис.4.12 Векторное поле главных (растягивающих) напряжений Рис.4.13 Траектории главных напряжений при изгибе и схема армирования железобетонной балки . Рис. 4.17 1 Рис.4.18 2 Рис. 4.19 3 Рис. 4.20 Эквивалентные напряжения по 3-ей и 4-ой теориям прочности Рис. 4.21 Эквивалентные напряжения по 3-ей теории прочности Рис. 4.24 Вертикальные перемещения верхней и нижней кромок балки, а также ее оси Рис. 4.21 Эквивалентные напряжения по 3-ей теории прочности Рис.4.22 Деформированный вид балкиполосы Рис. 4.23 Перемещения точек вертикальных торцевых волокон и волокон вблизи места приложения внешних сил Рис.4.25 Балка – полоса загружена силами по нижней кромке Рис.4.26 Нормальное напряжение Рис.4.27 Нормальное напряжение σy Рис. 4.28 Касательные напряжения Рис. 4.29 Главные напряжения Рис.4.30. Главные напряжения Рис. 4.31 Главные напряжения , Рис. 4.32 Приведенное напряжение Рис.4.33 Картина напряженного состояния Рис. 4.34 Потоки растягивающих напряжений Рис.4.35 Деформированный вид балки-полосы Рис.4.36 Перемещения точек верхней кромки, точек оси и точек нижней кромки балки-полосы Рис.4.37 Поперечные сечения вблизи места приложения нагрузки искривляются Задача Ляме Рис. 6.1* Длинный полый цилиндр Рис.6.2*. Действует только внутреннее давление Рис.6.3*. Действует только наружное давление равное σ Задача Головина Рис. 6.1 Чистый изгиб кривого бруса Рис. 6.2 Радиальные и тангенциальные напряжения Рис. 6.3 Эпюры радиальных и окружных напряжений Задача Кирша Рис.6.5. иллюстрация к задаче Кирша Рис. 6.6. Распределение растягивающих и сжимающих напряжений Рис. 6.7. Распределение растягивающих и сжимающих напряжений Изгиб плит Рис. 8.1 Пластина с эллиптическим жестко закрепленным контуром Рис.8.3 Изогнутая срединная поверхность плиты Рис.8.4 Линии уровня прогибов. Рис.8.5 Изгибающий момент Mx Рис. 8.6 Изгибающий момент Mx, и сечение 0-плоскостью M x(0,0) 2,75 кНм / м Wmax=W(0,0)=0.65857 мм M x(a,0) 3,05 кНм / м Рис. 8.7 Изгибающий момент My My(0,0)=6.41 кНм / м Рис. 8.8 My в точках контура My(0,b)=-12.20 кНм / м Рис.8.9 Крутящий момент H ( x, y ) Рис.8.10 Крутящий момент H ( x, y ) в точках контура Рис.8.11 Поперечная сила Qx ( x, y ) Рис.8.12 Поперечная сила Qx ( x a, y 0) Рис.8.13 Поперечная сила Qy ( x, y ) Рис.8.14. Распределение нормальных и касательных напряжений по толщине плиты Рис. 8.15 Напряжения max Рис. 8.16 Напряжения min Рис.8.18 Напряжения max , min в точках нижней поверхности (половина пластины) Рис.8.19 Картина напряженного состояния в точках нижней поверхности Рис.8. 20 Напряжения max , min в точках верхней поверхности (половина пластины) Рис. 8.21Картина напряженного состояния в точках верхней поверхности Рис.8.24 Функция прогиба Рис. 8.27 Напряжения max Рис.8.25 Крутящий момент Рис. 8.27 Напряжения min Рис.8.28 Поверхности max , min (на половине плиты) Рис.8.29 Картина напряженного состояния Рис.8.30 Направление главных площадок max Рис.8.31. Схема трещин (нижняя поверхность) Рис.8.32 На рис. 8.33 показана картина напряженного состояния на нижней поверхности плиты Рис.8.33 Картина напряженного состояния На рис.8.34 показаны поверхности главных напряжений 1 2 нижней поверхности плиты. Сопоставляя рис.8.33 и рис.8.34 делаем вывод; 1 2 3 в точках 3 Рис. 8.34 Главные напряжения в точках нижней поверхности плиты


