Задача Файлона
реклама

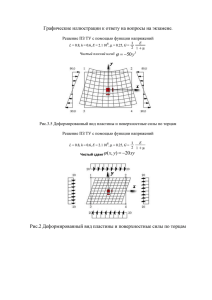
УДК 519.688.681.3 А. Н Аверин. ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ГИПОТЕЗ И ПРОВЕРКА ФОРМУЛ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ НА РЕШЕНИЯХ ЗАДАЧ ТЕОРИИ УПРУГОСТИ. АННОТАЦИЯ. На примерах решения задач теории упругости дается графическая иллюстрация допущениям, принимаемым в сопротивлении материалов при выводе основных формул плоского изгиба стержней. Решения задач выполняется в системе Maple. Рассмотрим балку-полосу длиной L, высотой h, толщиной δ. На балку-полосу по верхней и нижней кромкам действует три равномерно распределенных на малой площади a*δ нагрузки интенсивностью q, q/2, q/2. Они соответствуют действию на балку сосредоточенной силы F=q*a*δ и опорным реакциям Ra=Rb=F/2 (рис.1). Рис.1 Будем считать, что точки торцевых сечений пластины не перемещаются в вертикальном направлении, а горизонтальные перемещения возможны. На левой и правой кромках пластины нормальные напряжения σx равны нулю (граничные условия задачи Файлона.) [1]. Несложно показать, что вблизи точек левой и правой кромок пластины имеет место напряженное состояние чистого сдвига: x0, y0, xy0, x0, y0, xy0 . (1) Уравнение совместности деформаций плоской задачи теории упругости (ПЗТУ), заданное через функцию напряжений имеет вид 4 4 4 x4 2 y2 x2 y4 0 (2) . Решение уравнения (2) с учетом условий (1) будем искать в виде разложения в ряд по синусам mx m( y ) sin (3) a m 1 . Для функций перемещений точек срединной поверхности пластины в направлении координатных осей x и y имеем следующие представления: mx u um( y ) cos a m 1 , (4) . (5) mx v vm( y ) sin a m 1 Алгоритм решение поставленной задачи изложен в работе [1] . В данной статье представлены результаты вычислений по этому алгоритму и их графическая иллюстрация, полученные с помощью системы Maple [4]. Приведем результаты анализа напряженного состояния балки–полосы при следующих исходных данных:: L=120 см, h=30 см, δ=1 см, a= 2 см. Интенсивность равномерно распределенной нагрузки на участке малой площади по верхней кромке равна qB=5000 кГс/см2, а интенсивность опорных реакций qH= 2500 кГс/см2 . Распределенные нагрузки на малой площади a* δ=2 см2, соответствуют действию на балку-полосу сосредоточенной силы F=10000 кГс и опорных реакций Ra=Rb= 5000 кГс . Нагрузки, действующие на балку-полосу, разложим в ряд Фурье mx q( x ) qm sin a m 1 mm , (6) где коэффициенты разложения определяются по формулам a 2 qm a m x dx q( x ) sin a 0 . (7) Результаты аппроксимации функции нагрузки (приложенной по верхней и нижней кромкам пластинки рис.1) для нечетных значений m=1,3,…, 301 представлены на рис.2. Рис.2 Горизонтальные линии на рис.2 соответствуют заданным величинам интенсивности нагрузки, приложенной по верхней и нижней кромкам пластинки. Отметим, что приближение отрезком ряда Фурье дает хорошие результаты для периодической функции. В случае непериодической функции имеет место так называемый эффект Гиббса [3], который состоит в том, что значение аппроксимации на некоторых интервалах всегда превосходит значение исходной функции и вблизи точек разрыва имеют место колебания аппроксимации и рост погрешности. Оценка погрешности проводилась сравнением величин сосредоточенных сил F, Ra+Rb с соответствующими равнодействующими аппроксимированной нагрузки по верхней FB и нижней FH кромкам a a q ( x ) d x F q ( x ) d x ( FB ). B H H 0 0 , Погрешность по верхней кромке составила 0.03%, а по нижней 4%. Это объясняется тем, что функция аппроксимации нагрузки по нижней кромке при x<0 и x>a не определена. Для каждой амплитуды нагрузки с номером m записываем условия на поверхности. На верхней кромке пластинки (y=h) y qv , xy 0 m m m , (8) на нижней кромке пластинки (y=0) y qn , xy 0 m m m . (9) Из условий (8), (9) находим константы интегрирования, которые используются для определения амплитуд функции напряжений, нормальных и касательных напряжений и перемещений. На рис. 3 показана поверхность нормальных напряжений σx. На рис.4 представлены сечения поверхности напряжений (эпюры) вблизи места приложения нагрузки и на достаточном удалении от нее. Рис. 3 Нормальные напряжения σx Рис.4 Эпюры нормальных напряжений σx В сечении x=30 см в нижнем волокне пластины (y=0) σx=97.8 МПа, в верхнем (y=h) σx=-94.7 МПа, т.е. по высоте сечения закон изменения напряжений близок к линейному. По формулам сопротивления материалов в нижнем волокне σx=100. Мпа, в верхнем σx=-100. МПа. В сечении x=58 см (вблизи места приложения распределенной нагрузки) максимальное растягивающее напряжение возникает в нижнем волокне σx=188. МПа, а максимальное сжимающее напряжение достигается в волокне с координатой у=29.2 см σx=-249. МПа. Значения напряжений в середине пролета балки в нижнем и верхнем волокнах, вычисленные по формуле сопротивления материалов 200 Мпа и -200 Мпа. Таким образом, в сечении вблизи места приложения нагрузки решения сопротивления материалов и теории упругости имеют существенные различия. На рис.5,6 представлена поверхность нормальных напряжений σy и ее сечения вблизи места приложения нагрузки. В теории плоского изгиба стержней нормальные напряжения σy=0, т.е. используется гипотеза о ненадавливании продольных волокон [2]. Результаты вычислений, представленные на рис.5,6 показывают, что на достаточном удалении от места приложения внешних сил σy →0. Эти результаты наглядно подтверждают обоснованность принятой гипотезы. Рис.5 Напряжения σy Рис.6 Эпюры напряжений σy На рис.7 показана поверхность касательных напряжений τxy, а на рис.8 соответствующие эпюры. Вблизи места приложения нагрузки закон изменения напряжений существенно отличается от квадратной параболы. Максимальное значение напряжений в сечении пластины x=60.5 см достигается в точке с координатой y=29.2 см (вблизи верхней кромки пластины) и равно τxy =79.7 МПа. По формуле Журавского касательные напряжения по высоте сечения изменяются по закону квадратной параболы и наибольших значений достигают в точке с координатой у=15 см . Соответствующее напряжение τxy =25.0 МПа . На достаточном удалении от места приложения нагрузки в сечении x=75 см τxy =25.5 МПа (y=15 см) т.е имеет место хорошее совпадение с результатами, полученными по формуле сопротивления материалов.. Рис.7 Напряжения τxy Рис. 8 Эпюры напряжений τxy По известным значениям нормальных и касательных напряжений вычисляем главные напряжения в точках срединной поверхности пластины 1 1 1 max x y 2 2 2 x 2 x yy 4 xy 1 1 1 min x y 2 2 2 x 2 x yy 4 xy 2 2 2 2 2 , (10) 2 . Результаты вычислений представлены на рис. 9, 10. Рис.9 Напряжения max Рис.10 Напряжения min Напряжения max , min характеризуются не только своей интенсивностью, но и направлением. Угол между осью x и внешней нормалью к сечению, в котором действует напряжение max определяется из уравнения , xy tan( max ) maxx (11) . Положительное направление угла отсчитывается против хода часовой стрелки. Сечения (главные площадки), на которых действуют напряжения max , min взаимно перпендикулярны. Векторное поле главных напряжений строится следующим образом. Срединная плоскость пластинки разбивается на квадратные элементы (при симметричной нагрузке разбиение выполняется для половины пластинки). В окрестности центра каждого элемента строится квадрат, направление сторон которого совпадает с направлением главных площадок. Вектор главного напряжения направляется по внешней нормали к главной площадке, если напряжение растягивающее (положительно) и по внутренней, если напряжение сжимающее (отрицательное). Построенное таким образом векторное поле в дальнейшем будем называть картиной напряженного состояния (КНС). На (рис.11). КНС представлена для половины пластики на сетке 20*10. Рис.11 Картина напряженного состояния Из рис.11, что в точках вблизи приложения силы вдоль верхней кромки имеет место напряженное состояние - двухстороннее сжатие. По формулам сопротивления материалов в окрестности точек верхней кромки балки одностороннее сжатие (продольные волокна друг на друга не давят). Анализ (КНС) показывает, что в зоне приложения нагрузки имеет место двухстороннее сжатие позволяет правильно выбрать теорию прочности определиться На рис. 12,13 выделены векторные поля растягивающих и сжимающих напряжений Рис.12 Векторное поле главных растягивающих напряжений Рис.13 Векторное поле главных сжимающих напряжений Главные напряжения 3( 21 ) Рис. 15 1 Рис.17 2 Рис.18 3 На рис.10 показаны эквивалентные напряжения по 3-й теории прочности, а на рис.11 показаны эквивалентные напряжения по 4-й теории прочности. На рис 12 поверхность разности напряжений по 3-ей и 4-ой теориям прочности. Наибольшее расхождение в зоне двухстороннего сжатия На рис.11, 12 показаны потоки наибольших растягивающих напряжений ( на рис . 12 масштаб между длиной и высотой пластины принят 1:1). Это дает возможность правильно оценить размеры зоны двустороннего сжатия и действительное направление наибольших растягивающих напряжений Рис. 11 Рис. 12 Эквивалентные напряжения, вычисленные по гипотезе наибольших касательных напряжений представлены на рис. 13, а фрагмент поверхности вблизи места приложения сил на рис. 14 Рис. 13 Рис. 14 Эпюры эквивалентных напряжений представлены на рис.15. Результаты вычислений полученные по формулам сопротивления материалов хорошо согласуются в сечениях балки, находящихся на достаточном удалении от места приложения внешних сил и имеют существенное качественное и количественное отличие вблизи их приложения. Рис. 15 Отметим, что проведенный анализ напряженного состояния через функцию напряжений не зависят от упругих свойств изотропного линейно-упругого материала (E,μмодуля упругости и коэффициента Пуассона). Это означает, что полученное напряженное состояние можно переносить на геометрически подобные и аналогично загруженные детали конструкций, выполненные из другого материала [2]. Анализ деформированного состояния балки – пластины проведем при следующих упругих постоянных материала E=2.06e8 кН/м2 , =0.3. На рис. 16 показан деформированный вид балки-полосы. На рис 17. показаны перемещения точек вертикальных торцевых волокон и волокон вблизи места приложения внешних сил. Торцевые сечения остаются плоскими и после деформации балки, а сечения вблизи приложения сил искривляются, т.е. гипотеза плоских сечений, принимаемая в сопротивлении материалов не выполняется. Рис.16 Рис. 17 На рис.18 показаны вертикальные перемещения верхней и нижней кромок балки, а также ее оси. Из рис.18 видно, что наибольшие перемещение получает точка верхней кромки балки в месте приложения силы. Перемещения нижней кромки меньше чем перемещения оси. В сопротивлении материалов, балка закрепляется на уровне оси и считается, что перемещения точек верхней и нижней кромок балки одинаковые и равны перемещениям соответствующих точек оси. На достаточном удалении от места приложения силы Рис. 18 решение линейного дифференциального уравнения оси изогнутой балки хорошо согласуется с решением плоской задачи теории упругости. БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 1. Александров А.В., Потапов В.Д. Сопротивление материалов. Основы теории упругости и пластичности. М. :Высшая школа, 2002.-399 c. 2. Александров А.В. , Потапов В.Д., Державин Сопротивление материалов. М.: Высшая школа, 2000.-559 c. 3. Хеминг Р.В. Численные методы. М.: Наука, 1972. 4.Говорухин В. , Цибулин В. Компьютер в математическом исследовании. Учебный курс. Maple, MATLAB, LaTex. СПБ: Питер, 2001. 624 с.