Задача 1 Дано Решение: углом

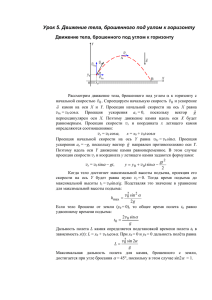
Задача 1. Струя воды в гидромониторе вылетает из ствола со скоростью 50 м/ с под
углом 30° к горизонту. Найти дальность полета и наибольшую высоту
подъема струи.
Дано:
Решение:
𝜐0 = 50 м/ с Выберем прямоугольную систему координат x0y с началом отсчета в
точке О вылета струи. Вдоль оси 0x движение равномерное
α = 30°
прямолинейное, так как на струю воды
Найти:
действует только сила тяжести,
h- ?
направленная вертикально вниз. Вдоль
l- ?
оси 0у струя воды движется
равнозамедленно до верхней точки
траектории (точки А), а вниз –
равноускоренно с ускорением
свободного падения, направленным
вертикально вниз в любой точке
траектории. С учетом этого, управления
движения струи воды имеют вид:
0x: x= 𝜐0𝑥 t
𝑔𝑡 2
0y: y= 𝜐0𝑦 t 2
Скорость движения струи по оси 0у до точки А (вершина параболы)
изменяется по закону:
𝜐𝑦 = 𝜐0𝑦 – gt , где 𝜐0𝑦 = 𝜐0 sin 𝛼
Для точки А 𝜐𝑦 = 0; y = h; t = 𝑡1 , где 𝑡1 - время движения дл максимальной
точки.
Тогда формула примет вид:
0 = 𝜐0𝑦 − 𝑔𝑡1 , откуда 𝜐0𝑦 = 𝑔𝑡1 или 𝜐0 sin 𝛼 = 𝑔𝑡1
Следовательно 𝑡1 =
𝜐0 ∗sin 𝛼
𝑔
Найдем высоту подъема струи: ℎ = 𝜐0𝑦 𝑡1 −
𝜐0 2 ∗ sin2 𝛼
=
2
= 𝜐0 ∗ sin 𝛼 ∗
𝜐0 2 ∗ sin2 𝛼
𝑔2
𝜐0 2 ∗ sin2 𝛼
ℎ=
𝑔𝑡1
2𝑔
2𝑔
;ℎ=[
м2 /𝑐 2
м/𝑐 2
= м]
Для точки падения струи воды (точки В) на землю
t = 𝑡1 ; y=0; x=1.
Следовательно, уравнение координаты у примет вид:
0 = 𝜐0𝑦 t 2 −
𝑔𝑡2 2
𝑔𝑡2 2
2
𝜐0𝑦 t 2 =
, откуда время полета струи:
2
2𝑣0𝑦 2𝜐0 ∗ sin 𝛼
𝑡2 =
=
𝑔
𝑔
Найдем дальность полета:
𝑙 = 𝜐0𝑥 𝑡2 , 𝜐0𝑥 = 𝜐0 ∗ cos 𝛼
2𝜐0 ∗ sin 𝛼
𝑙 = 𝜐0 ∗ cos 𝛼 ∗
𝑔
2
2𝜐0 ∗ cos 𝛼 ∗ sin 𝛼 𝑣0 2 ∗ sin 2𝛼
𝑙=
=
𝑔
𝑔
𝜐0 ∗sin 𝛼
𝑔
𝑔
− ∗
2
Так как 2cos 𝛼 sin 𝛼 = sin 2𝛼.
Найдем числовые значения h и l:
502 ∗ sin2 30° 502 ∗ 0,52
ℎ=
=
≈ 32 м
2 ∗ 9,8
2 ∗ 9,8
502 ∗ sin 60 °
𝑙=
≈ 221 м
9,8
Ответ:
ℎ ≈ 32 м
𝑙 ≈ 221 м
Задача 2. Под каким углом к горизонту надо бросить тело, чтобы высота его
подъема была равна дальности полета?
Дано:
Решение:
Высоту подъема тела {Задача 1) можно определить по формуле:
h=l
𝜐0 2 ∗ sin2 𝛼
ℎ=
2𝑔
Найти: Дальность полета:
2𝜐0 2 ∗ cos 𝛼 ∗ sin 𝛼
α- ?
𝑙=
𝑔
По условию задачи h = l, следовательно:
𝜐0 2 ∗ sin2 𝛼 2𝜐0 2 ∗ cos 𝛼 ∗ sin 𝛼
=
2𝑔
𝑔
Откуда sin 𝛼 = 2 ∗ 2 cos 𝛼
sin 𝛼
И следовательно,
= 4 или t𝑔 𝛼 = 4.
cos 𝛼
Найдем угол α: 𝛼 = 𝑎𝑟𝑐𝑡𝑔4 ≈ 76° ≈ 1,3 рад.
Ответ: α ≈ 76°
Задача 3. Под каким углом надо бросить тело, чтобы дальность полета была
наибольшей?
Дано:
Решение:
Дальность полета определяется формулой (задача 1):
𝑙=
𝑣0 2 ∗ sin 2𝛼
𝑙=
𝑙𝑚𝑎𝑥
𝑔
Дальность полета будет максимальна при наибольшем значении sin 2𝛼, то
Найти: есть
α- ?
sin 2𝛼 = 1
Отсюда
𝜋
2𝛼 = arcsin 1 = рад
2
𝜋
𝜋
2𝛼 = => 𝛼 = или 45о
2
Ответ: α =
𝜋
4
4
= 45о
Задача 4. В какой точке траектории летящий снаряд обладает наименьшей
скоростью?
Решение:
Наименьшая скорость снаряда будет в наивысшей точке траектории, так как в этой
точке вертикальная составляющая скорости (𝜐𝑦 ) равна нулю и скорость
определяется только горизонтальной составляющей (𝜐𝑘 ), которая одинакова во всех
точках траектории.
Задача 5. Как направлено ускорение снаряда после выстрела из ствола орудия, если
сопротивление воздуха отсутствует? Как изменится это направление при
наличии сопротивления воздуха?
Решение:
Если отсутствует сопротивление воздуха, то ускорение снаряда одинаково во всех
точках траектории и направлено вертикально вниз. Это ускорение равно ускорению
свободного падения. При наличии сопротивления воздуха ускорение отклонено от
вертикали в направлении противоположном движению снаряда.
Задача 6. Тело, брошенное под углом к горизонту, находилось в полете 4 секунды.
Какой наибольшей высоты достигло тело?
Дано:
Решение:
Время полета тела определим по формуле:
2𝜐 ∗sin 𝛼
l= 4с
𝑡= 0
(Задача 1)
𝑔
Наибольшая высота подъема тела:
Найти:
𝜐0 2 ∗ sin2 𝛼
ℎ=
h- ?
2𝑔
решим систему из двух уравнений:
2𝜐0 ∗ sin 𝛼
𝑔𝑡 2
𝑔
2
=> (𝑣0 ∗ sin 𝛼) = ( )
𝜐0 2 ∗ sin2 𝛼
2
ℎ=
2𝑔
{
𝑔2 𝑡 2
𝑔2 𝑡 2
2
2
𝑣0 ∗ sin 𝛼 =
=> ℎ =
4
4 ∗ 2𝑔
𝑡=
𝑔𝑡 2
м∗с2
Откуда ℎ = ; ℎ = [ 2 = м]
8
с
Вычислим:
9,8 ∗ 42 9,8 ∗ 4 ∗ 4
ℎ=
=
= 9,8 ∗ 2 = 19,6 м.
8
8
Ответ: h = 19,6 м.
Задача 7. Мальчик бросил горизонтально мяч из окна, расположенного на высоте 15
м. Сколько времени летел мяч до земли и с какой скоростью он был
брошен, если мяч упал на расстоянии 5,3 м от основания дома?
Дано:
Решение:
h = 15 м; Для описания движения выберем прямоугольную систему координат х0у,
l=5,3м;
ось у направим вертикально вниз. За начало отсчета координат О примем
g = 9,8
точку бросания мяча.
2
Уравнения движения мяча:
м/с
0x: x = 𝜐0𝑥 t
2
Найти: 0y: y = 𝜐 t + 𝑔𝑡
0𝑦
2
t-?
По условию задачи 𝜐0𝑦 = 0; 𝜐0𝑥 = 𝜐0 ,
𝑣0 −?
следовательно:
x = 𝜐0 t
𝑔𝑡 2
y=
2
В момент приземления
y = h; x = l.
Тогда определим время полета и начальную
скорость:
2ℎ
м
𝑔
м/с2
𝑡 = √ ; 𝑡 = [√
= с]
𝑙
𝑡
Вычислим:
𝑣0 =
2 ∗ 15 √30
𝑡=√
=
≈ 1,7 с
9,8
9,8
𝑣0 =
𝑙 √𝑔
√2ℎ
=
5,3∗√9,8
√2∗15
≈ 3 м/с или
5,3
м
≈3
1,7
с
Ответ: 𝑡 ≈ 1,7 с, 𝑣0 ≈ 3 м/с
𝑣0 =
Задача 8. Шарик, движущийся по столу со скоростью 1 м/с, упал, скатившись на
расстояние 0,45 м от стола. Какова высота стола?
Дано:
Решение:
𝑣0 = 1 м/с За начало отсчета координат примем точку, где
мяч падал со стола, а за 0 начало отсчета времени
l=S=
— момент сбрасывания. Ось х направим
0,45 м
горизонтально, а ось у — вертикально вверх.
Движение шарика описывается уравнениями:
Найти:
0x: x = 𝜐0𝑥 t
h-?
𝑔𝑡 2
0y: y = −
2
знак «-» перед проекцией g, так как направление
вектора 𝑔⃗ противоположно направлению оси у).
В момент падения шарика на пол:
у = - h; х = l.
Из первого уравнения можно определить время падения шарика: 𝑡 =
Следовательно, высота, с которой падал шарик:
−ℎ = −
𝑔𝑡 2
2
2
=> ℎ =
𝑔𝑡 2
2
=
𝑔𝑡 2
2𝑣02
ℎ=[
м∗м2
с2 ∗ м2 /с2
𝑙
𝑣0
= м]
0,45 ∗ 9,8
= 0,992 м ≈ 1 м
2∗1
Ответ: высота стола ℎ ≈ 1 м
ℎ=
Задача 9. Почему бомба, сброшенная с горизонтально летящего самолета, не падает
вертикально вниз?
Решение:
Бомба, как и самолет, имеет скорость в горизонтальном направлении и в момент
отрыва от самолета вследствие инерции удерживается в этом состоянии движения.
Задача 10. Снаряд вылетает из горизонтально направленного ствола пушки с
некоторой скоростью. С какой скоростью вылетел бы тот же снаряд из той
же пушки, если бы выстрел был произведен также горизонтально на
поверхности Марса, сила притяжения которого составляет 0,38 силы
притяжения Земли? Трением в стволе пушки пренебречь.
Решение:
Скорость движения снаряда зависит от величины силы, действующей на снаряд, и от
массы снаряда, но не зависит от силы тяжести. Более слабое притяжение Марса
повлияло бы на дальность полета снаряда и на форму его траектории движения.
Поэтому снаряд будет вылетать из пушки с одинаковой скоростью и на Марсе, и на
Земле.
Задача 11.Тело брошено со скоростью V0 под углом α к горизонту. Определите
максимальную скорость подъема тела, время его полета, дальность полета,
скорость с какой тело упадет на землю и угол, который составляет вектор
скорости с горизонтом в точке падения тела на землю.
Дано
Решение:
V0,α,g
V,H,t, H = V0t - gt2/2 V0x = V0cosα
V0y = V0sinα Vy = V0y - gt
t = V0y/g = v0sinα/g
S,µ-? H = (V0y)2/g - g(V0y)2/2g = (V0y)2/2g = (V0)2sin2α/2g
H = (V0)2sin2α/2g t = tвверх + tвниз
H = g(tвниз)2/2
(V0)2sin2α/2g = g(tвниз)2/2 tвниз = V0sinα/g
tвверх = tвниз t = 2t вверх= 2tвниз = 2*V0sinα/g
S = V0xt = V0cosα*2*V0sinα/g = (V0)2*sin2α/g
S = (V0)2*sin2α/g
Vx = V0x= V0cosα
Vy = g tвниз = V0sinα
V = V0
tgµ = Vy/Vx = V0sinα/ V0cosα = tgα; µ = α
Задача 12. Кошка прыгает с подоконника высотой 1,2 метра горизонтально со
скоростью 6 метров в секунду. На какое расстояние от стены она
окажется на момент приземления.
Дано
Решение:
g =9.8 м/с2
S=V0t
V0=6 м/с
H=1,2 м
S-?
𝑆 = 𝑉0 √
H=gt2/2
2𝐻
𝑔
𝑆 = 6√
t=√
2∗1.2
9.8
2H
g
=3м
Ответ: S=3 м
Задача 13. С башни в горизонтальном направлении бросили камень с начальной
скоростью 10 метров в секунду. Камень упал на расстоянии 40 метров
от основания башни. Сколько времени камень находился в полете?
Дано
Решение:
𝑆
V0=10 м/с
𝑆 = 𝑉0 ∗ 𝑡
S=40м
𝑡=
t= 4 c
t-?
Ответ: t= 4 c
𝑉0
Задача 14. С вышки бросили камень в горизонтальном направлении. Через 2
секунды камень упал на землю на расстоянии 30 метров от вышки. С
какой скоростью он упал?
Дано
Решение:
2
g=10 м/с
S=V0*t
S=30 м
Vx= V0= S/t =15м/с t = 2 c Vy = gt = 20м/с
V-?
𝑉 = √𝑉𝑥2 + 𝑉𝑦2 = 25 м/с
Ответ: V=25 м/с
Задача 15. Шарик катился по гладкой горизонтальной поверхности стола со скорость
2 метра в секунду. Докатившись до края стола, шарик падает на пол на
расстоянии 0,8 метров от основания стола. С какой высоты упал шарик?
Дано
Решение:
2
g=10 м/с
S = V*t, V = V0 t = S/V0= 0.4 м/с
S=0,8 м
V=2 м/с
H-?
𝐻=
𝑔𝑡 2
2
= 0.8м
Ответ: H=0.8 м
Задача 16. Камень брошен горизонтально с некоторой высоты. Через 3 секунды его
скорость оказалась направленной под углом 45 градусов к горизонту.
Найдите начальную скорость камня.
Дано
Решение:
t=3 c
𝑉𝑦
g=9.8 м/с2
Vx=V0 ;
Vy= gt; 𝑡𝑔𝛼 =
α=45
0
𝑉𝑥 =
𝑉𝑦
𝑡𝑔𝛼
𝑉𝑥
= 𝑔𝑡 = 30м/с
V0-?
Ответ: V0=30м/с
Задача 17. Тело брошено под углом 60 градусов к горизонту со скоростью 20
метров в секунду. Под каким углом к горизонту направлено тело через 1,5
секунды.
Дано
Решение:
0
α=60
Vx=V0x=V0cosα Vy=V0y - gt=V0sinα - gt
V0=20м/с
t=1.5c
𝑉𝑦
𝑉 𝑠𝑖𝑛𝛼−𝑔𝑡
20∗0.87−14.7
µ-?
𝑡𝑔𝛼 = = 0
=
= 0.27
𝑉𝑥
𝑉0 𝑐𝑜𝑠𝛼
10
0
µ= arctg µ=11.3
Ответ: µ =11,30
Задача 18. Тело брошено под углом 60 градусов к горизонту со скоростью 20 метров
в секунду. Через сколько времени и на какой высоте оно будет иметь
скорость направленную под углом 450 к горизонту.
Дано
Решение:
0
α=60
h = V0yt - gt2/2,
β=450
h = V0sinαt - gt2/2 = 9.6м
V0=20м/с V0x= V0cosα, V0y= V0sinα
t-? H-?
Vy= V0sinα - gt;
𝑉𝑦
𝑉 𝑠𝑖𝑛𝛼−𝑔𝑡
Vx= V0cosα; 𝑡𝑔𝛽 = = 0
𝑡=
𝑉0 𝑠𝑖𝑛𝛼−𝑡𝑔𝛽𝑉0 𝑐𝑜𝑠𝛼
𝑔
𝑉𝑋
𝑉0 𝑐𝑜𝑠𝛼
= 0.71c
Ответ: h = 9.6м; t = 0.71c
Задача 19. Два мальчика играют в мяч, бросая его друг другу. Какой наибольшей
высоты достигнет мяч во время игры, если он от одного игрока к другому
летит 2с?
Дано
Решение:
t=2 c
g=9.8 м/с2
H-?
𝐻=
𝑔𝑡 2
2
= 4,9м
Ответ: H = 4.9м
Задача 20. Снаряд вылетел из дальнобойной пушки со скоростью 1000м/с под
углом 30 градусов к горизонту. На каком расстоянии от пушки снаряд
упадет на землю?
Дано:
Решение:
V0=1*103м/с
𝑆=
α=300
S-?
𝑉02 𝑡𝑔2𝛼
𝑔
=
106 ∗0.87
9.8
= 0.89*105 = 89км
Ответ: S = 89км
Задача 21.Из окопа на уровне земли под углом 45 градусов к горизонту бросили
гранату с начальной скоростью 9,8 метров в секунду. Каково расстояние
между точками бросания и падения?
Дано:
Решение:
V0=9,8 м/с
α=450
S-?
𝑆=
𝑉02 𝑡𝑔2𝛼
𝑔
=
96,04∗sin 90
= 9.8*1= 9.8км
9.8
Ответ:S=9,8км
Задача 22. Под каким углом к горизонту брошено с поверхности земли камень, если
известно, что дальность его полета в 4 раза больше высоты.
Дано:
Решение:
S=4h
α-?
S=V0xt; Vy=V0y-gt ;t=V0y/g
V0x=V0cosα; V0y=V0sinα;ℎ =
𝑡 = 2𝑡 =
2𝑉0𝑦
𝑔
; 𝑆 = 𝑉0𝑥 ∗
2𝑉02 𝑐𝑜𝑠𝛼
∗ 𝑠𝑖𝑛𝛼 = 4 ∗
Ответ: α = 450.
2
𝑉𝑦2 +𝑉𝑘𝑦
=
2
𝑉0𝑦
𝑔
2𝑔
2𝑉0𝑦 2𝑉02 𝑐𝑜𝑠𝛼∗𝑠𝑖𝑛𝛼
;
𝑔
2
𝑉0 𝑠𝑖𝑛2 𝛼
𝑔
=4
𝑉02 𝑠𝑖𝑛2 𝛼
𝑔
cosα = sinα; tgα =1 => α=450
Задача 23. На некоторой высоте из одной точки одновременно бросили 2 шара: один
вверх, а другой вниз, оба со скоростью 40 метров в секунду под углом 60
градусов к горизонту. На каком расстоянии будут находиться шары друг
от друга через 2 секунды?
Дано:
Решение:
V0=40 м/с
h=h1+h2;
α=600
g=9.8м/с2
h-?
𝑔𝑡 2
ℎ = 𝑉0𝑦 𝑡 −
+ 𝑉0𝑦 𝑡 +
2
ℎ = 2𝑉0 𝑐𝑜𝑠𝛼𝑡 = 80км
Ответ: h = 80км
𝑔𝑡 2
2
= 2𝑉0𝑦 𝑡
Задача 24. Тело движется с постоянным ускорением и проходит одинаковые,
следующие друг за другом расстояния по 15 метров за время 2 секунды и 1с
соответственно. Найдите ускорение.
Дано:
Решение:
t1=2c
V1=V0+at1
S1=V0t1+at12/2
𝑆2 = 𝑉1 𝑡2 +
t2=1c
1
S1 = S2 = S =15м
2
a-?
𝑎𝑡12
𝑎𝑡22
2
=> 𝑆2 = 𝑉0 𝑡2 + 𝑎𝑡1 𝑡2 +
𝑎𝑡22
𝑎𝑡22
2
𝑉0 𝑡1 +
= 𝑉0 𝑡2 + 𝑎𝑡1 𝑡2 +
2
2
2V0 t1+ at12 = 2V0t2 + 2at1t2 + at22
4V0+4a = 2V0+4a+a
𝑎
2V0 = a =>V0 =
𝑎
𝑆1 = 𝑡1 +
2
2
𝑎 2
𝑎
𝑡1 = (𝑡1
2
2
а = 5м/с2
Ответ: a = 5м/с2
+ 𝑡12 ) => 𝑎 =
2𝑆
𝑡1 +𝑡12