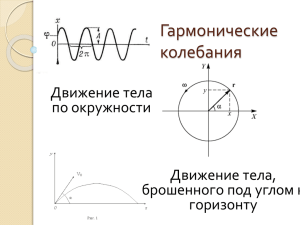
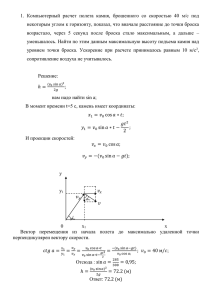
Движение тела, брошенного под углом к горизонту
реклама

Урок 5. Движение тела, брошенного под углом к горизонту Движение тела, брошенного под углом к горизонту Y r vx r r v0y v0 αr y0 0 v0x x0 A r g B X Рассмотрим движение тела, брошенного под углом α к горизонту с r r начальной скоростью v 0 . Спроецируем начальную скорость v 0 и ускорение r a камня на оси X и Y. Проекция начальной скорости на ось X равна r v0x = v0 cosα. Проекция ускорения ax = 0, поскольку вектор g перпендикулярен оси X. Поэтому движение камня вдоль оси X будет равномерным. Проекция скорости vx и координата x летящего камня определяются соотношениями: vx = v0 cosα, x = x0 + v0t cosα Проекция начальной скорости на ось Y равна v0y = v0 sinα. Проекция r ускорения ay = −g, поскольку вектор g направлен противоположно оси Y. Поэтому вдоль оси Y движение камня равнопеременное. В этом случае проекция скорости vy и координата y летящего камня задаются формулами: gt 2 2 Когда тело достигнет максимальной высоты подъема, проекция его скорости на ось Y будет равна нулю vy = 0. Тогда время подъема до максимальной высоты t1 = v0sinα/g. Подставляя это значение в уравнение для максимальной высоты подъема: vy = v0 sinα − gt, y = y 0 + v 0 t sin α − v 2 sin 2 α hmax = 0 2g Если тело брошено от земли (y0 = 0), то общее время полета t0 равно удвоенному времени подъема: 2 v sin α t0 = 0 g Дальность полета L камня определяется подстановкой времени полета t0 в зависимость x(t): L = x0 + v0 t0cosα. При x0 = 0 и y0 = 0 дальность полёта равна v 02 sin 2α L= g Максимальная дальность полета для камня, брошенного с земли, достигается при угле бросания α = 45°, поскольку в этом случае sin2α = 1. Уравнение траектории Определим, по какой траектории движется брошенное тело, то есть найдем уравнение, связывающее между собой координаты тела по осям x и y. Для этого выразим время из зависимости x(t): x − x0 t= v 0 cos α и подставим его в формулу для y(t). Получаем квадратичную функцию y(x): 2 ⎛ x − x0 ⎞ g ( x − x0 ) 2 1 ⎛ x − x0 ⎞ ⎟⎟ sin α − g ⎜⎜ ⎟⎟ = y 0 + ( x − x0 ) tgα − y = y 0 + v 0 ⎜⎜ 2 ⎝ v 0 cos α ⎠ 2v 02 cos 2 α ⎝ v 0 cos α ⎠ Если выбрать систему координат таким образом, что x0 = 0, y0 = 0, то формула упрощается: y = xtgα − gx 2 2 v 02 cos 2 α Графиком полученной функции y = y(x) является парабола (см. рис.), направленная ветвями вниз и пересекающая ось x в точках x1 = 0 (начало v 02 sin 2α . Координаты вершины этой параболы равны координат) и x2 = L = g v 2 sin 2 α xв = L/2 и yв = hmax = 0 . 2g y yв x х1 хв х2 Пример. Два тела брошены одновременно: одно с земли под углом к горизонту, а другое − горизонтально с высоты H = 10 м над землей. Вначале тела находились на одной вертикали, а через некоторое время столкнулись в полете (см. рис.). Известно, что если бы тела не столкнулись, то брошенное с земли тело пробыло бы в полете вдвое дольше другого. Найдите высоту, на которой произошло столкновение. Сопротивлением воздуха пренебречь. 2 H 1 Решение. Если бы тела не сталкивались, то время полета второго тела, брошенного горизонтально, было бы равно t2 = 2 H g . Пpи этом время полета первого тела было бы pавно, согласно условию, t1 = 2t2 = 2 2 H g . С другой стороны, t1 = 2v 0 y g , где v0y − вертикальная составляющая начальной скорости первого тела. Находим, что v0 y = 2 gH . В системе отсчета, связанной со вторым телом, первое равномерно приближается ко второму со скоростью v0y, поэтому время от начала полета тел до их столкновения равно t ст = H v 0 y . В земной системе отсчета уравнение движения первого тела имеет вид h1 (t ) = v 0 y t − gt 2 / 2 , откуда находим, что столкновение тел происходит на высоте 3H 2 h1 (t ) = v 0 y t ст − gt ст /2 = = 7,5 м . 4 Пример. Тело брошено под углом α = 30° к горизонту с начальной скоростью v0 = 20 м/с. Через какое время вектор скорости тела окажется перпендикулярен начальной скорости? Решение. Запишем в векторном виде зависимость скорости свободно падающего тела от времени: r r r v = v 0 + gt r r Строим треугольник скоростей, учитывая, что по условию задачи v ⊥ v 0 (см. рис.) r v0 α r v0x r gt r v α По теореме Пифагора получаем, что (gt)2 = v2 + v 02 . Отсюда выражаем искомое время: t= v 02 + v 2 g r Горизонтальная составляющая v 0 x скорости тела не изменяется, поэтому из рисунка следует, что v0cosα = vsinα, откуда v = v0ctgα. Подставляя это выражение, получаем ответ: t= v 02 + v 02 ctg 2α v v = 1 + ctg 2α = g g g sin α Задачи для самостоятельного решения. Задача 1. Тело брошено вдоль склона вниз под углом α к поверхности горы. Определить дальность полёта, если начальная скорость равна v0, угол наклона горы β. Сопротивлением воздуха пренебречь. [Ответ: 2 v 02 sin α cos(α − β ) g cos 2 β ] Задача 2. Пушка выстреливает ядро под углом α = 60° к горизонту со скоростью v = 100 м/с. Когда ядро достигает наивысшей точки траектории, пушка стреляет второй раз. Через какое время после первого выстрела ядра окажутся на минимальном расстоянии друг от друга (пока оба ядра в полете)? Чему равно это расстояние? Сопротивлением воздуха пренебречь. [Ответ: t = vsinα/(2g) ≈ 4,42 c, L = v2cosαsinα/g ≈ 442 м]