РГР2_614
реклама

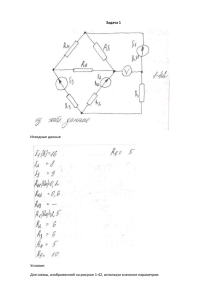
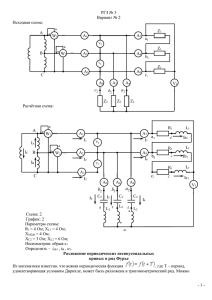
Национальный исследовательский «Томский политехнический университет» Факультет АВТ Кафедра ТОЭ Теоретические основы электротехники Расчетно-графическая работа №2 Расчет линейной цепи синусоидального тока Вариант №614 Выполнил студент группы 8В83 __________ Проверил Е.Ю. Чистяков О.В. Васильева Томск 2010 Задание: 1. В исходной цепи с ЭДС e(t ) 2 E sin( t ) рассчитать токи ветвей и составить баланс мощностей (активных и реактивных). Коэффициент связи k = 0,9. Взаимная индуктивность M k L1 L2 . Записать уравнения Кирхгофа для мгновенных значений без развязки 2. 3. 4. 5. 6. 7. 8. индуктивной связи. Переписать уравнения в комплексной форме и найти все токи и показание вольтметра. Произвести развязку индуктивной связи. Определить все токи методом контурных токов. Определить ток в ветви с индуктивностью L2 методом эквивалентного генератора; Записать мгновенные значения токов и напряжений и построить их волновую диаграмму. Построить в одних осях векторные диаграммы токов (лучевую) и напряжений (топографическую). Определить показание электродинамического вольтметра аналитически и по топографической диаграмме. Подтвердить расчеты пунктов 1, 3 ,проделав работу в среде ElectronicsWorkbench. Составить схему с автотрансформатором. E,В R, Ом 22 35 Таблица значений: C, L1, , МкФ Гн град 300 0 0.2 2 L2 , Гн F, Гц 0.2 50 1. Выполняем первый пункт задания В исходной цепи с ЭДС e(t ) 2 E sin( t ) рассчитаем токи ветвей. Взаимная индуктивность M k L1L2 . Для этого запишем для одного из узлов по первому закону Кирхгофа, а для двух контуров по второму закону Кирхгофа равенства: I1 I 2 I 3 0 I 3 ( R jX C ) I 2 ( R jX L 2 ) I 1 jX m 0 I ( R jX ) I ( R jX ) I jX E 3 2 L1 C M 1 1 1 A jX M R jX L1 1 ( R jX L 2 ) R jX C А jX M R jX C 0 B 0 E Находим токи: 0.36 - 0.107j J A 1 B 0.249 - 2.397j *10 -3 A 0.112 - 0.105j 0.376 J 0.49 A 0.153 Баланс мощностей: Полная мощность: S EJ * 1 7,928 2,352 j ВА Активная мощность: P I 1 R I 2 R I 3 R 7.928 Вт 2 2 2 Реактивная мощность: Q I 1 X L 2 I 2 ( X L 2 ) I 3 ( X C ) 2 X M I 1 I 2 cos(arg( I 1 ) arg( I 2 )) 2.352 2 2 2 3 Вар 2. Выполняем второй пункт задания Произведем развязку индуктивной связи: R jXL1-jXM jXM R E jXL2-jXM R Рис. 1. Схема с развязкой индуктивной связи. 4 -jXC 3. Выполняем третий пункт задания Определим эквивалентные сопротивления ветвей схемы: Рис. 2. Схема с эквивалентными сопротивлениями. Z 1 R j X L1 j X M 35 6.283 j Ом Z 2 R j X L 2 j X M 35 6.283 j Ом Z 3 j X M j X C R 35 45.938 j Ом Используем метод контурных токов: J 1K (Z 1 Z 2 ) J 2 K (Z 2 ) E J 2 K (Z 2 Z 3 ) J 1K (Z 2 ) 0 Z1 Z 2 A Z2 Z2 E B Z2 Z3 0 0.36 0.107 j А J A 1 B 0.112 0.105 j Находим токи в ветвях: I 1 J 1 0.36 0.107 j А I 1 0.376 А I 2 J 1 J 2 0.249 2.397 j 10 А I 2 0.249 А I 3 J 2 0.112 0.105 j А I 3 0.153 А 3 Токи сходятся. 5 4. Выполняем четвертый пункт задания Метод эквивалентного генератора Рис. 3. Метод эквивалентного генератора. K1 E 0.202 0.151 j А Z1 Z 3 U XX K 1 Z 3 13.987 4.003 j В Находим сопротивление генератора: Z Г I2 U XX 0.249 2.397 j А ZГ Z2 6 Z1 Z 3 21.108 10.364 j Ом Z1 Z 3 5. Выполняем пятый пункт задания Мгновенные значения токов: i1(t ) 2 I 1 sin( t arg( I 1 )) i 2(t ) 2 I 2 sin( t arg( I 2 )) i3(t ) 2 I 3 sin( t arg( I 3 )) i1(t ) 2 I 1 e jarg( I 1 ) i 2(t ) 2 I 2 e jarg( I 2 ) i3(t ) 2 I 3 e А А jarg( I 3 ) А Рис. 4. Волновая диаграмма токов. Находим мгновенные значения напряжений: Представляем сопротивления в показательном виде: Z 1 35.560 e j 0.178 Z 2 35.560 e j 0.178 Z 3 57.752 e j 0.92 Находим напряжения: u1(t ) i1(t ) Z 1 2 I 1 e jarg( I 1 ) 35.560 e j 0.178 18.904 sin( t 0.110 180 u 2(t ) i 2(t ) Z 2 2 I 2 e jarg( I 2 ) 35.560 e j 0.178 12.501 sin( t 0.168 u3(t ) i3(t ) Z 3 2 I 3 e jarg( I 3 ) 50.826 e j 0.168 12.501 sin( t 0.168 7 ) 180 180 ) ) Итак, получили: u1(t ) 18.904 sin( t 6.303) u 2(t ) 12.501 sin( t 9.626) u3(t ) 12.501 sin( t 9.626) 0 E U1 E I1 R E I 1 R I 1 jX L1 E I R I jX I jX 1 1 2 L1 M 0 I 2R U2 I 2 R I 2 jX L 2 I R I jX I jX 2 1 L2 M 2 0 U3 I 3 ( jX C ) I ( jX ) I R 3 C 3 Рис. 5. Волновая диаграмма напряжений. 8 Выбираем масштаб: m 25 Составляем матрицы (лучевая и топографическая диаграммы): 0 I1 m I1 0 I 2 m I2 0 I 3 m I3 Рис. 6. Векторная диаграмма токов и напряжений. 9 6. Выполняем шестой пункт задания Определяем показания электродинамического вольтметра: а) аналитически Uv E I 1 R 9.387 3.742 j В Uv 10.105 В б) по топографической диаграмме (рис. 6) 0 V В Uv 2 Im U3 2 Re U3 2 2 9.809 Im U2 1.102 2 Re U2 2 9.809 1.102 9.871 10 7. Выполняем седьмой пункт задания Рис. 7. Схема, собранная в Electronics Workbench. Токи, найденные в Workbench, сходятся с аналитически найденными токами. 11 8. Выполняем восьмой пункт задания Рис. 8. Схема с автотрансформатором. Вывод: нахождение значений переменных токов является сложной задачей, т.к. требуется решать интегро-дифференциальные уравнения. Переход к комплексным значениям значительно упрощает задачу. научились работать с комплексными токами, строить графики токов/напряжений и векторные диаграммы, иллюстрирующие правильность полученных результатов. Те же результаты были получены и в Workbench. Workbench дает некоторую погрешность при вычислении значений переменных токов, но тем не менее позволяет проверить правильность проведенных вычислений. В схеме с автотрансформатором мы получаем большую погрешность изза того, что мы рассматриваем идеальную индуктивность, не имеющую сопротивления. 12