*** *1 - Reshaem.Net

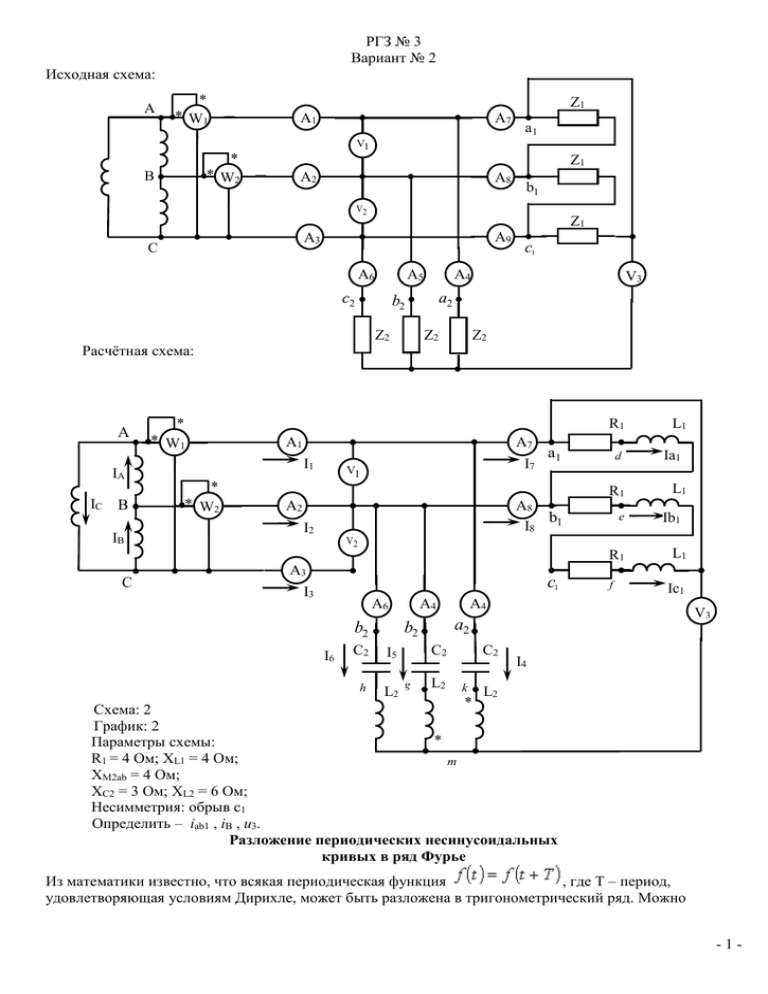
РГЗ № 3
Вариант № 2
Исходная схема:
A
*
* W1
Z1
A1
A7
a1
V1
*
* W2
B
Z1
A2
A8
b1
V2
Z1
A9
A3
C
A6
A5
c2
A4
V3
a2
b2
Z2
c1
Z2
Z2
Расчётная схема:
A
*
* W1
R1
A1
I1
IA
IC
B
IB
A7
*
* W2
I7
V1
a1
d
R1
A8
b
I8 1
A2
I2
e
V2
R1
C
A3
c1
I3
A6
C2
I5
h
L2
L1
Ib1
L1
Ic1
A4
C2
g
Ia1
V3
a2
b2
b2
I6
A4
f
L1
L2
C2
k
*
I4
L2
Схема: 2
График: 2
*
Параметры схемы:
R1 = 4 Ом; XL1 = 4 Ом;
m
XM2ab = 4 Ом;
XC2 = 3 Ом; XL2 = 6 Ом;
Несимметрия: обрыв с1
Определить – iab1 , iB , u3.
Разложение периодических несинусоидальных
кривых в ряд Фурье
Из математики известно, что всякая периодическая функция
, где Т – период,
удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно
-1-
отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с
чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
(1)
.
Здесь
- постоянная составляющая или нулевая
гармоника;
- первая (основная) гармоника,
изменяющаяся с угловой частотой
, где Т – период
несинусоидальной периодической функции.
В выражении (1)
коэффициенты
и
, где
определяются по формулам
;
. Свойства периодических кривых, обладающих симметрией
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или
в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих
симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры
гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при
вычислениях.
1. Кривые, симметричные относительно оси абсцисс. К данному типу относятся кривые,
удовлетворяющие равенству
(см. пример на рис. 2). В их разложении
отсутствуют постоянная составляющая и четные гармоники, т.е.
.
2. Кривые,
симметричные
относительно оси
ординат. К данному
типу относятся
кривые, для которых
выполняется
равенство
(см.
пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е.
.
3. Кривые, симметричные относительно начала координат. К этому типу относятся кривые,
удовлетворяющие равенству
(см. пример на рис. 4). При разложении таких
кривых отсутствуют постоянная и косинусные составляющие, т.е.
.
Производим разложение вручную, по известным формулам. У нас на кривой будет функция f(t)
=100 на интервале 0 ÷ 10 мс и f(t) = -100 в интервале 10 ÷ 20 мс. Отсюда находим коэффициенты с
-2-
учетом что из-за симметрии выпадают нулевая и чётные гармоники. Период функции T = 20 мс, частота
f = 1/T = 50 Гц, круговая частота ω = 2πf = 314,159 рад/c, am = 100.
10
20
2
𝑏1 = ∙ (∫ 𝑎𝑚 sin(𝜔 ∙ 𝑡) + ∫ 𝑎𝑚 sin(𝜔 ∙ 𝑡)) = 127.324
𝑇
0
10
10
20
2
∙ (∫ 𝑎𝑚 sin(3 ∙ 𝜔 ∙ 𝑡) + ∫ 𝑎𝑚 sin(3 ∙ 𝜔 ∙ 𝑡)) = 42.441
𝑇
0
10
Построим график с точностью да первых трёх гармоник:
𝑏3 =
f( t)  b1 sin( w t)  b3 sin( 3 w t)
125
100
75
50
25
f( t )
25 0
50
75
100
125
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
0.05
t
(1)
𝐸̇𝐴
Определение показания приборов:
Первая гармоника:
Запишем комплексные фазные и линейные напряжения:
𝑏1 𝑗∙30𝑜
𝑜
=
∙𝑒
= 77.97 + 45.016 ∙ 𝑗 = 90.032 ∙ 𝑒 𝑗∙30
√2
(1)
𝐸̇𝐵 =
(1)
𝐸̇𝐶 =
𝑏1
√2
𝑏1
√2
𝑜
𝑜
∙ 𝑒 −𝑗∙90 = −90.032 ∙ 𝑗 = 90.032 ∙ 𝑒 −𝑗∙90
𝑜
𝑜
∙ 𝑒 𝑗∙150 = −77.97 + 45.016 ∙ 𝑗 = 90.032 ∙ 𝑒 𝑗∙150
Комплексны сопротивления ветвей:
𝑜
𝑍1 = 𝑅1 + 𝑗 ∙ 𝑋𝐿1 = 4 + 4 ∙ 𝑗 = 5.657 ∙ 𝑒 𝑗∙45
𝑜
𝑍2 = 𝑗 ∙ 𝑋𝐿2 − 𝑗 ∙ 𝑋𝐶2 = 6 − 3 ∙ 𝑗 = 3 ∙ 𝑗 = 3 ∙ 𝑒 𝑗∙90
Расчёт токов:
( )
( )
( )
𝐼4̇ 1 + 𝐼5̇ 1 + 𝐼6̇ 1 = 0
̇ − 𝑗 ∙ 𝑋𝑚 ∙ 𝐼5(1)
̇ − 𝑍2 ∙ 𝐼6(1)
̇ = −𝐸̇𝐶(1)
{𝑍2 ∙ 𝐼4(1)
(1)
(1)
(1)
(1)
−𝑗 ∙ 𝑋𝑚 ∙ 𝐼4̇ + 𝑍2 ∙ 𝐼5̇ − 𝑍2 ∙ 𝐼6̇ = 𝐸̇𝐵
Матричная форма:
(1)
0
𝐼4̇
1
(1)
(1)
−𝑍2 ] ∙ [𝐼5̇ ] = [−𝐸̇𝐶 ]
(1)
−𝑍2
(1)
𝐸̇𝐵
𝐼6̇
Решаем через обратную матрицу:
1
[ 𝑍2
−𝑗 ∙ 𝑋𝑚
1
−𝑗 ∙ 𝑋𝑚
𝑍2
-3-
(1)
𝐼4̇
1
(1)
̇
[𝐼5 ] = [ 𝑍2
−𝑗 ∙ 𝑋𝑚
(1)
𝐼6̇
1
−𝑗 ∙ 𝑋𝑚
𝑍2
0
1 −1
(1)
−𝑍2 ] ∙ [−𝐸̇𝐶 ]
(1)
−𝑍2
𝐸̇
𝐵
Записываем токи:
(1)
𝐼4̇ = −10.289 − 13.366 ∙ 𝑗 = 16.868𝑒 −𝑗∙127.589
(1)
𝐼5̇ = −16.72 − 2.228 ∙ 𝑗 = 16.868𝑒 −𝑗∙172.411
(1)
𝐼6̇ = 27.009 + 15.594 ∙ 𝑗 = 31.188𝑒 𝑗∙30
Находим токи в других ветвях:
(1)
𝐼9̇
(1)
𝐸̇𝐴
=
= 15.373 − 4.119 ∙ 𝑗 = 15.915𝑒 −𝑗∙15
𝑍2
(1)
̇
𝐼10
(1)
−𝐸̇𝐴
=
= −7.687 + 2.06 ∙ 𝑗 = 7.958𝑒 𝑗∙165
2 ∙ 𝑍2
(1)
(1)
(1)
̇ = 23.06 − 6.179 ∙ 𝑗 = 23.873𝑒 −𝑗∙15
𝐼7̇ = 𝐼9̇ − 𝐼10
(1)
(1)
̇ − 𝐼9(1)
̇ = −23.06 + 6.179 ∙ 𝑗 = 23.873𝑒 𝑗∙165
𝐼8̇ = 𝐼10
(1)
(1)
(1)
(1)
(1)
(1)
(1)
(1)
𝐼1̇
= 𝐼4̇ + 𝐼7̇ = 12.77 − 19.545 ∙ 𝑗 = 23.347𝑒 −𝑗∙56.84
𝐼2̇ = 𝐼5̇ + 𝐼8̇ = −39.78 + 3.951 ∙ 𝑗 = 39.976𝑒 𝑗∙174.328
𝐼3̇ = 𝐼6̇ = 27.009 + 15.594 ∙ 𝑗 = 31.188𝑒 𝑗∙30
Расчёт токов на 3-ей гармонике:
Независимо от способа соединения – в звезду или в треугольник – линейные напряжения не содержат
гармоник, кратных трем.
При соединении в звезду это объясняется тем, что гармоники, кратные трем, образуют нулевую
последовательность, ввиду чего исчезают из линейных напряжений, равных разности фазных.
При соединении в треугольник составляющие фазных ЭДС, кратные трем, не выявляются в линейных
(фазных) напряжениях, так как компенсируются падениями напряжений на собственных
сопротивлениях фаз генератора.
Комплексное значение ЭДС действующих в обмотках генератора:
(3)
(3)
(3)
𝐸̇𝐴 = 𝐸̇𝐵 = 𝐸̇𝐶 = 𝐸̇ (3) =
𝑐3
𝑜
𝑒 𝑗∙90 = 30.01 = 11.254𝑒 𝑗∙180
√2
Сопротивление обмоток генератора:
𝑜
𝑍Об = 𝑅Об + 3 ∙ 𝑗 ∙ 𝜔 ∙ 𝐿Об = 0.5 + 1.499 ∙ 𝑗 = 1.58 ∙ 𝑒 𝑗∙71.548
Токи в обмотках трансворматора:
(3)
(3)
(3)
𝐼𝐴̇ = 𝐼𝐵̇ = 𝐼𝐶̇ = 𝐼 (̇ 3) =
𝐸̇ (3)
= 6.013 − 18.02 ∙ 𝑗 = 18.997𝑒 −𝑗∙71.548
𝑍Об
-4-
Записываем показания приборов:
Ампертметры:
(1)
𝐼𝐴1 = |𝐼1̇ | = 23.347 𝐴
(1)
𝐼𝐴2 = |𝐼2̇ | = 39.976 𝐴
(1)
𝐼𝐴3 = |𝐼3̇ | = 31.188𝐴
(1)
𝐼𝐴4 = |𝐼4̇ | = 16.868 𝐴
(1)
𝐼𝐴5 = |𝐼5̇ | = 16.868 𝐴
(1)
𝐼𝐴6 = |𝐼6̇ | = 31.188 𝐴
(1)
𝐼𝐴7 = |𝐼7̇ | = 23.873 𝐴
(1)
𝐼𝐴8 = |𝐼8̇ | = 23.873 𝐴
𝐼𝐴9 = 0 𝐴
Вольтметры:
(1) 2
𝑈𝑉1 = √𝐸𝐴
(1) 2
𝑈𝑉2 = √𝐸𝐵
2
+ 𝐸 (3) = 94.902 𝐵
2
+ 𝐸 (3) = 94.902 𝐵
(1)
𝑈𝑉3 = |𝑍2 ∙ 𝐼4̇ | = 50.604 𝐵
Ваттметры:
(1)
(1)
(1)
(1)
𝑃𝑊1 = 𝑅𝑒(−𝐸̇𝐶 ∙ 𝐼̃1 ) = |−𝐸̇𝐶 | ∙ |𝐼1̇ | ∙ cos (φ𝐸̇(1) − φ𝐼̇(1) ) = 1875.546 Вт
1
𝐶
(1)
(1)
(1)
(1)
𝑃𝑊2 = 𝑅𝑒(𝐸̇𝐵 ∙ 𝐼̃2 ) = |𝐸̇𝐵 | ∙ |𝐼2̇ | ∙ cos (φ𝐸̇(1) − φ𝐼̇(1) ) = −355.728 Вт
𝐵
2
Мгновенные значения величин из таблицы:
(1)
𝑖9 (𝑡) = √2 ∙ |𝐼9̇ | ∙ sin (𝜔 ∙ 𝑡 + φ𝐼̇(1) ) = 20.508 sin(100 ∙ 𝜋 ∙ 𝑡 − 15𝑜 )
9
(3)
𝑖𝐵 (𝑡) = √2 ∙ |𝐼𝐵̇ | ∙ sin (𝜔 ∙ 𝑡 + φ𝐼̇(3) ) = 26.866 sin(100 ∙ 𝜋 ∙ 𝑡−71.548𝑜 )
𝐵
(1)
𝑢3 (𝑡) = √2 ∙ |𝑍2 ∙ 𝐼4̇ | ∙ sin (𝜔 ∙ 𝑡 + φ𝑍
̇(1)
2 ∙𝐼4
) = 71.564 sin(100 ∙ 𝜋 ∙ 𝑡−37.589𝑜 )
Построим графики:
-5-
30
20
50
10
iab1( t )
u3( t )
iE2( t )
0
0.01
0.02
0.03
0.04
10
50
20
30
t
Рассчитываем напряжения на всех элементах схемы и строим диаграмму:
Ur1a1  r1 I91
Ur1a1  61.493  16.477i
Ur1a1  63.662
arg( Ur1a1)  15 deg
Ul1a1  Xl1 j I91
Ul1a1  16.477  61.493i
Ul1a1  63.662
arg( Ul1a1)  75deg
Ur1b1  r1 I101
Ur1b1  30.746  8.238i
Ur1b1  31.831
arg( Ur1b1)  165deg
Ul1b1  Xl1 j I101
Ul1b1  8.238  30.746i
Ul1b1  31.831
arg( Ul1b1)  105 deg
Ur1c1  r1 I101
Ur1c1  30.746  8.238i
Ur1c1  31.831
arg( Ur1c1)  165deg
Ul1c1  Xl1 j I101
Ul1c1  8.238  30.746i
Ul1c1  31.831
arg( Ul1c1)  105 deg
Ul2a2  Xl2 j I41
Ul2a2  80.197  61.736i
Ul2a2  101.207
arg( Ul2a2)  37.589 deg
Uc2a2   Xc2 j I41
Uc2a2  40.099  30.868i
Uc2a2  50.604
arg( Uc2a2)  142.411deg
Umab   Xm j I51
Umab  8.911  66.881i
Umab  67.472
arg( Umab)  97.589deg
Ul2b2  Xl2 j I51
Ul2b2  13.366  100.321i
Ul2b2  101.207
arg( Ul2b2)  82.411 deg
Uc2b2   Xc2 j I51
Uc2b2  6.683  50.16i
Uc2b2  50.604
arg( Uc2b2)  97.589deg
Umba   Xm j I41
Umba  53.465  41.157i
Umba  67.472
arg( Umba)  142.411deg
Ul2c2  Xl2 j I61
Ul2c2  93.564  162.057i
Ul2c2  187.127
arg( Ul2c2)  120deg
Uc2c2   Xc2 j I61
Uc2c2  46.782  81.028i
Uc2c2  93.564
arg( Uc2c2)  60 deg
-6-
Первая гармоника
Масштабы:
10 В/см
3,125 А/см
Третья гармоника
-7-