2. расчет электрических цепей постоянного тока
реклама

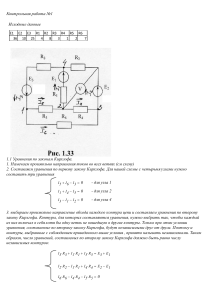
1. СОСТАВ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ Пояснительная записка должна содержать следующие структурные элементы в приведенной последовательности: – титульный лист; – содержание; – введение; – задание по расчету электрической цепи постоянного тока; – расчетная схема в соответствии с вариантом; – расчетная часть; – схема моделирования на компьютере с помощью программы EWB; – задание по расчету электрической цепи переменного тока; – расчетная схема в соответствии с вариантом; – расчетная часть; – схема моделирования на компьютере с помощью программы EWB; – заключение; – список используемой литературы. Общий объем пояснительной записки должен составлять 10–15 листов формата А4. Введение должно содержать краткую характеристику рассчитываемых схем, сравнение и обоснование методов расчетов. В заключение пояснительной записки приводится оценка полученных результатов, а также сравнение теоретических и экспериментальных данных. 2. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА 2.1. Схема электрической цепи Для схемы, представленной на рис. 2.1, определить токи в каждой ветви, составить баланс мощностей, построить потенциальную диаграмму для контура, содержащего не менее двух ЭДС. Задачу решить с помощью законов Кирхгофа, а также методами контурных токов, узловых напряжений и эквивалентного генератора. Результат проверить путем составления баланса мощностей. 1 R5 S1 S2 S3 S4 S5 S6 S7 E1 E2 E3 R7 R1 R2 R3 Рис. 2.1 №, Вар. Е1, В Е2, В Е3, В R1, Ом R2, Ом R3, Ом R5, Ом R7, Ом 21 150 230 130 0,2 0,2 0,4 2 3 S1 1 Положение выключателей S2 S3 S4 S5 S6 0 1 1 1 0 S7 0 Примечание: 1 – выключатель замкнут, 0 – разомкнут. 3. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА 3.1. Схема электрической цепи Для схемы электрической цепи, приведенной на рис. 3.1, выполнить следующее: 1) рассчитать комплексы действующих значений токов во всех ветвях, воспользовавшись методом узловых потенциалов; 2) построить топографическую диаграмму комплексных потенциалов точек схемы, совмещенную с векторной диаграммой токов; 3) составить баланс активных и реактивных мощностей. 2 C1 L3 Е1 L2 C2 1 Е3 2 S1 L1 R2 C3 Рис. 3.1 №, Вар. 21 E1 Амплитуда, f, В Гц 150 75 φ, град. 130 E2 Амплитуда, f, В Гц 230 75 φ, град. 60 L1, мГн C1, мкФ L2, мГн C2, мкФ L3, мГн C3, мкФ R2, Ом Положение S1 34 29 – 32 38 60 18 2 УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЭЛЕКТРОННЫХ ПРИБОРОВ 3 БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Стафеев, А.В. Электротехника: учеб. пособие / А.В. Стафеев. – Хабаровск: Изд-во ДВГУПС, 2006. 2. Бессонов, Л.А. Теоретические основы электротехники: электрические цепи: учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов / Л.А. Бессонов. – 7-е изд., перераб. и доп. – М.: Высш. шк., 1978. – 528 с. 3. Бессонов, Л.А. Сборник задач по теоретическим основам электротехники / Л.А. Бессонов. – М.: Высш. шк., 2000. – 528 с. 4. Прянишников, В.А. Электротехника и ТОЭ в примерах и задачах / В.А. Прянишников. – М.: Высш. шк., 2003. – 336 с. 5. Электротехника и электроника в экспериментах и упражнениях: практикум на Electronics Workbench. В 2 т. / Д.И. Панфилов [и др.] ; под общ. ред. Д.И. Панфилова. – М.: ДОДЭКА, 2000. – 288 с. 6. Карлащук, В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её применение / В.И. Калащук. – М.: Солон-Р, 2000. – 506 с. 4 4. ПРИМЕРЫ ВЫПОЛНЕНИЯ РАСЧЕТОВ 4.1. Линейная электрическая цепь постоянного тока Для схемы электрической цепи, приведенной на рис. 4.1, выполнить следующее: 1) составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы и решить ее, используя программу MathCAD; 2) рассчитать токи во всех ветвях схемы методом контурных токов (МКТ); 3) рассчитать токи во всех ветвях схемы методом узловых потенциалов; 4) составить баланс мощностей, вычислив суммарную мощность источников и суммарную мощность приемников; 5) рассчитать ток I1, используя теорему об активном двухполюснике и эквивалентном генераторе; 6) начертить потенциальную диаграмму для любого замкнутого контура, включающего оба источника ЭДС. B I6 R6 R2 I11 R5 A I1 I2 m E2 I5 R1 D I33 E1 I22 I4 R4 Исходные данные: R1 = 9 Ом R2 = 20 Ом R3 = 16 Ом R4 = 40 Ом R5 = 30 Ом R6 = 22 Ом Е1 = 8 В Е2 = 30 В Е3 = 10 В R3 f I3 n E3 C Рис. 4.1 В этой схеме (рис. 4.1) количество узлов: n = 4; ветвей: m = 6; контуров: k = 3. 4.1.1. Система уравнений на основании законов Кирхгофа Выбираем направления токов в ветвях произвольно. Количество уравнений, необходимых по законам Кирхгофа: 5 –по первому закону: n – 1 = 4 – 1 = 3; –по второму закону: k = 3; –общее количество уравнений: 6. По первому закону Кирхгофа: –для узла «А»: –I3 – I5 – I6 = 0; –для узла «В»: –I1 + I2 + I6 = 0; –для узла «С»: I1 + I3 + I4 = 0. По второму закону Кирхгофа: –для контура 1: –I2R2 – I5R5 + I6R6 = –E2; –для контура 2: –I3R3 + I4R4 + I5R5 = –E3 – E1; –для контура 3: I1R1 + I2R2 – I4R4 = E2. Запишем систему уравнений, подставив числовые значения: –I3 – I5 – I6 = 0; – I1 + I2 + I6 = 0; I1 + I3 + I4 = 0; – 20I2 – 30I5 + 22I2 = –30; –16I3 + 40I4 + 30I5 = –10 – 8 = –18; 9I1 + 20I2 – 40I4 = 30. Поскольку решение системы уравнений с шестью неизвестными является достаточно трудоемкой задачей, воспользуемся математической программой MathCAD. Снимок с экрана компьютера приведен на рис. 4.2. 6 Рис. 4.2 Окончательно получаем: I1 = 0,051 A, I2 = 0,612 A, I3 = 0,382 A, I4 = – 0,432 A, I5 = 0,8 A, I6 = –0,562 A. 4.1.2. Расчет методом контурных токов Выберем направления контурных токов произвольно. Число уравнений, которые необходимо составить для расчета токов в ветвях схемы, всегда равно числу независимых контуров. В данной схеме три независимых контура, поэтому имеем следующую систему: I11R11 + I22R12 + I33R13 = E11 I11R21 + I22R22 + I33R23 = E22 I11R31 + I22R32 + I33R33 = E33, где I11, I22, I33 – контурные токи, которые необходимо определить; R11, R22, R33 – суммарные сопротивления первого, второго и третьего контуров соответственно; E11, E22, E33 – алгебраическая сумма ЭДС соответственно первого, второго и третьего контуров, причем если направление ЭДС сов7 падает с направлением контурного тока, то ЭДС берется со знаком плюс, а если не совпадает, то со знаком минус. Сопротивления с разными индексами – это взаимные сопротивления, входящие одновременно в состав двух контуров, причем знак взаимного сопротивления берется положительным, если направления контурных токов в нем совпадают, и отрицательным – если нет. Тогда: R11 = R2 + R5 + R6 = 20 + 30 + 22 = 72 Ом; R22 = R3 + R4 + R5 + R6 = 16 + 40 + 30 = 86 Ом; R33 = R1 + R2 + R4 = 9 + 20 + 40 = 69 Ом; R12 = R21 = –R5 = –30 Ом; R13 = R31 = –R2 = –20 Ом; R23 = R32 = –R4 = –40 Ом; E11 = –E2 = –30 В; E22 = –E3 – E1 = –10 – 8= –18 В; E33 = E2 = 30 В. Подставим найденные значения в систему уравнений: 72I11 – 30I22 – 20I33 = –30; –30I11 + 86I22 – 40I33 = –18; –20I11 – 40I22 + 69I33 = 30. Решая эту систему, находим контурные токи. Воспользуемся правилом Крамера. В общем виде контурные токи определяются: I11 = Δ11/Δ, I22 = Δ22/Δ, I33 = Δ33/Δ, где Δ – определитель (детерминант) системы; Δ11, Δ22, Δ33 – частные определители, которые получаются в результате замены соответствующего столбца на значения ЭДС. 72 30 20 30 86 40 = 72 · 86 · 69 – 72 · 40 · 40 – 30 · 40 · 20 – 30 · 30 · 69 – 20 40 69 – 20 · 30 · 40 – 20 · 86 · 20 = 167548. 30 30 20 72 30 20 11 18 86 40 = –94080, 22 30 18 40 = –63924, 30 40 69 20 30 69 72 30 30 33 30 86 18 = 8520. Для контурных токов получаем значения: 20 40 30 I11 = Δ11/Δ = –94080/167548 = –0,5615 А, I22 = Δ22/Δ = –57876/167548 = – 0,3815 А, I33 = Δ33/Δ = 8520/167548 = 0,0508 А. Далее выразим истинные токи через контурные. Ток в ветви, принадлежащей двум или нескольким контурам, равен алгебраической сумме со8 ответствующих контурных токов. Со знаком плюс берутся контурные токи, совпадающие с током этой ветви, со знаком минус – не совпадающие с ним. I1 = I33 = 0,0508 A; I2 = I33 – I11 = 0,0508 + 0,5615 = 0,6123 A; I3 = –I22 = 0,3815 A; I4 = I22 – I33 = –0,3815 – 0,0508 = –0,4324 A; I5 = I22 – I11 = –0,3815 + 0,5615 = 0,18 A; I6 = I11 = –0,5615 A. 4.1.3. Расчет методом узловых потенциалов (МУП) Выберем в качестве базисного узел «D» и его потенциал приравняем к нулю φD = 0. Необходимо найти потенциалы узлов «А», «В» и «С». Схема с заземленным узлом «D» показана на рис. 4.3. B I6 R6 I1 R2 I2 m R5 A I5 R1 D E1 I4 f E2 R4 R3 n I3 E3 C Рис. 4.3 Вычислим собственные проводимости узлов «А», «В» и «С». Расчеты необходимо производить с возможно большей точностью. Gaa Gbb 1 1 1 1 1 1 0,141288 См ; R3 R5 R6 16 30 22 1 1 1 1 1 1 0,206566 См ; R1 R2 R6 9 20 22 9 1 1 1 1 1 1 0,198611 См . R1 R3 R4 9 16 40 Общая проводимость этих узлов: 1 1 Gab Gba 0,045455 См ; R6 22 Gcc Gac Gca 1 1 0,0625 См ; R3 16 Gbc Gcb 1 1 0,111111 См . R1 9 Находим узловые токи: – в узле «А»: I aa – в узле «B»: I bb E3 E1 10 8 1,125 A ; R3 16 E2 30 1,5 A ; R2 20 E3 E1 10 8 1,125 A . R3 16 Составим систему уравнений для нахождения потенциалов узлов по методу узловых напряжений: Gaaa Gabb Gacc I aa ; – в узле «С»: I cc Gbaa Gbbb Gbcc I bb ; Gcaa Gcbb Gccc I cc . Подставим числовые значения: 0,141288 a 0,045455b 0,0625c 1,125 ; 0,045455 a 0,206566b 0,111111 c 1,5 ; 0,0625 a 0,111111b 0,198611 c 1,121 . Решая эту систему с помощью правила Крамера (п. 4.1.2), находим потенциалы узлов: φa 5,388 В, φb 17,736 В, φc 17,282 В. Рассчитаем токи в ветвях, выбирая предварительно их условные положительные направления, как в схеме при расчете методом контурных токов: c 17,736 17,282 I1 b 0,0504 A ; R1 9 10 I2 I3 d b E2 R2 a c E3 E1 R3 I4 d c R4 I5 I6 5,388 17,282 10 8 0,3816 A ; 16 0 17,282 0,4321 A ; 40 a d R5 a b R6 0 17,736 30 0,6132 A ; 20 5,388 0 0,1796 A ; 30 5,388 17,736 0,5613 A . 22 4.1.4. Расчет баланса мощностей Суммарная мощность источников: Pист E2 I 2 ( E3 E1 ) I3 30 0,6123 (10 8) 0,3815 25,236 Вт . Суммарная мощность приемников: Pпр I12 R1 I 22 R2 I32 R3 I 42 R4 I52 R5 I62 R6 25,234 Вт Допускается расхождение баланса активных мощностей 0,5 %: Pист Pпр 100% 25,236 25,243 100% 0,008% 0,5% P 25,236 Pист 4.1.5. Потенциальная диаграмма контура «CDmBAfn» Под потенциальной диаграммой понимают распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме. За нулевой потенциал примем потенциал узла «С». φс = 0. Рассчитаем потенциалы других точек схемы: d с I 4 R4 0 ( 0,4324) 40 17,296 В; m d E2 17,296 30 12,704 В; b m I 2 R2 12,704 0,6123 20 0,458 В; a b I 6 R6 0,458 ( 0,5614) 22 11,8928 В; 11 f a E1 11,8928 8 3,8928 В; n f I 3 R3 3,8928 0,3815 16 9,9968 В; c n E3 9,9968 10 0,0032 0 В. График потенциальной диаграммы показан на рис. 4.4. φ, В 14 m 12 10 8 6 4 2 b C R, Ом C 0 -2 f -4 -6 -8 n -10 -12 a -14 -16 d -18 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 Рис. 4.4 4.1.6. Моделирование схемы с помощью программы Electronics Workbench (EWB) Для проверки результатов теоретических расчетов произведем моделирование исследуемой схемы методом физического моделирования. Соберем схему (рис. 4.1) в среде Electronics WorkBench. Снимок с экрана компьютера с показаниями амперметров представлен на рис. 4.5. 12 Рис. 4.5 Как видно из рис. 4.5, показания приборов совпадают со значениями, полученными в предыдущих пунктах. Таким образом, токи рассчитаны правильно. 4.2. Линейная электрическая цепь переменного тока Для схемы электрической цепи, приведенной на рис. 4.6, выполнить следующее: 1) рассчитать комплексы действующих значений токов во всех ветвях, воспользовавшись методом узловых потенциалов; 2) построить топографическую диаграмму комплексных потенциалов точек схемы, совмещенную с векторной диаграммой токов. При этом потенциал точки а, указанной на схеме, принять равным нулю; 3) составить баланс активных и реактивных мощностей. 13 e k C1 a L3 e′1 R2 f m e″3 h L1 Исходные данные: L1 = 4 мГн L3 = 109 мГн C1 = 33 мкФ C3 = 95 мкФ R2 = 65 Ом f = 70 Гц e′1 = 141sin(ωt – 90º) В e″3 = 282sin(ωt – 50º) В C3 b d Рис. 4.6 4.2.1. Расчет методом узловых потенциалов В первую очередь необходимо от мгновенных значений ЭДС перейти к комплексам действующих значений ЭДС: . 0 141 j 900 ' 0 e1 141sin( t 90 ) E '1 e 99,7e j 90 j 99,7 B ; 2 . 0 282 j 500 " 0 e3 282 sin( t 50 ) E "3 e 199,4e j 50 128,17 j152,75B . 2 Любой узел схемы можно заземлить. Токораспределение при этом не изменится. Схема с комплексными ЭДС и заземленным узлом b показана на рис. 4.7. Круговая частота: ω = 2πf = 2π·70 = 439,82 рад/с. Сопротивления реактивных элементов цепи: X L1 L1 439,82 14 103 6,16 Ом ; X L 3 L3 439,82 109 103 47,94 Ом ; 14 X С1 1 1 68,9 Ом ; 6 С1 439,82 33 10 X С3 1 1 23,93 Ом . С3 439,82 95 10 6 e k C1 a L3 İ3 ′ Ė1 R2 ″ f İ1 Ė İ2 m 3 h L1 C3 d b Рис. 4.7 Комплексные сопротивления ветвей, Ом, _ Z 1 j ( X L1 X C1 ) j (6,16 68,9) j 62,74 62,74e j 90 Ом ; 0 _ Z 2 R2 65 Ом ; _ Z 3 j ( X L 3 X C 3 ) j ( 47,94 23,93) j 24,01 24,01e j 90 Ом . 0 Соответственно комплексные проводимости ветвей: _ Y1 1 _ Z1 1 62,74e j 90 _ Y2 1 _ Z2 _ Y3 1 _ Z3 0,015939e j 90 j0,015939 См ; 0 0 1 24,01e j 90 1 0,015385 См ; 65 0,041649e j 90 j0,041649 См . 0 0 При использовании комплексных величин электрические схемы переменного тока можно рассчитывать любыми методами, которые используются при расчете схем на постоянном токе. . Пусть b 0 , тогда по методу двух узлов (частный случай метода узловых потенциалов) имеем: 15 _ . e _ _ _ E 1 Y 1 E 3 Y 3 ' _ " _ _ Y 1 Y 2 Y 3 j 99,7 j 0,015939 (128,17 j152,75) ( j 0,041649) j 0,015939 0,015385 j 0,041649 4,772767 j5,338152 7,16067e j131,8 j 72, 6960 0 238,992 e j 59,104 0,015385 j 0,02571 0,029962e (71,086 j 228,175) В. 0 Токи в ветвях находятся по обобщенному закону Ома: _ . . I1 e E'1 _ Z1 71,086 j 228,175 ( j 99,7) 146,83e j 61,044 0 0 62,74e j 90 62,74e j 90 0 2,34e j 28,956 (2,047 j1,133), А 0 . . I2 e _ Z2 _ . . I3 e E" 3 _ Z3 0 71,086 j 228,175 (1,094 j 3,51) 3,677e j 72,689 , А 65 71,086 j 228,175 (128,17 j152,75) 57,084 j 75,425 0 0 24,01e j 90 24,01e j 90 3,939e j 217,12 (3,142 j 2,378), A 0 Правильность расчета можно проверить, если найденные значения токов подставить в уравнения, составленные по первому и второму законам Кирхгофа. Уравнения, составленные по законам Кирхгофа для данной схемы, имеют вид: . . . I1 I 2 I 3 0 . . _ . _ ' I 1 Z 1 I 2 Z 2 E 1 . _ . . _ I 2 Z 2 I 3 Z 3 E" 3 . Проверим первое уравнение системы: . . . I1 I 2 I 3 0 ; (2,047 j1,133) (1,094 j 3,51) ( 3,142 j 2,378) 0 ; ( 0,001 j 0,001) 0 . 16 Проверим второе уравнение системы: _ . . _ . I 1 Z1 I 2 Z 2 E'1 ; ( 2,047 j1,133) ( j 62,74) (1,094 j 3,51) 65 ( j 99,7) ; j128,429 71,084 71,11 j 228,15 j 99,7 ; 0,026 j 99,721 j 99,7 . Проверим третье уравнение системы: _ . . _ . I 2 Z 2 I 3 Z 3 E" 3 ; (1,094 j 3,51) 65 ( 3,142 j 2,378) j 24,01 (128,17 j152,75) ; 71,11 j 228,15 j 75,44 51,1 (128,17 j152,75) ; (128,21 j152,71) (128,17 j152,75) . Как видно, все уравнения дают тождества, а небольшие неточности обусловлены округлением величин при вычислениях. 4.2.2. Построение топографической диаграммы Примем потенциал точки a равным нулю (φа = 0). Найдем потенциалы других точек схемы: . a 0 ; . . . . k e a ( jX C1 ) I1 0 ( j 68,9) (2,047 j1,133) (78,064 j141,038), В . . . m k jX L 3 I 3 (78,064 j141,038) j 47,94 ( 3,142 j 2,378) (192,065 j 9,589), В . . . h m E3" (192,065 j9,589) (128,17 j152,75) (63,895 j162,339), В . . . . d b e R2 I 2 (78,064 j141,038) 65 (1,094 j 3,51) (6,954 j87,112), В . . . f a E1" 0 ( j99,7) j99,7, В Теперь построим топографическую диаграмму комплексных потенциалов точек схемы, совмещенную с векторной диаграммой токов (рис. 4.8). 17 j 170 φh jX C 3İ 3 150 Ė 90 3 jX ″ φf L1 110 İ3 130 φb,φd 70 İ3 ·20, А 50 Ė′1 30 İ1 ·20, А φm 10 + -10 İ3 -30 -jX L3 -R2İ2 İ1 C1 -jX -50 -70 İ2 · 20, А -90 -110 -130 -150 -70 φe,φk -50 -30 -10 10 30 50 70 90 110 130 150 170 190 210 Рис. 4.8 4.2.3. Расчет баланса активных и реактивных мощностей Найдем сопряженные комплексы токов * I 1 (2,047 j1,133) 2,34e j 28,956 , А ; * 0 I 2 (1,094 j3,51) 3,677e j 72,689 , А ; 18 0 * I 3 ( 3,142 j 2,378) 3,939e j 217,12 , А . 0 Найдем полную суммарную мощность источников: ~ . . * * S E I 1 E I 3 99,7e j 90 2,34e 28,956 199,4e j 50 3,939e j 217,12 ' 1 " 3 0 0 0 0 233,298e j 61,044 785,437e j167,12 112,95 j 204,134 765,67 j175,082 0 0 (878,62 j 29,052), ВА Суммарная активная мощность источников: ~ P Re[ S ] Re[878,62 j 29,052] 878,62, Вт . ист Суммарная активная мощность приемников: P I 22 R2 3,677 2 65 878,821, Вт . пр Допускается расхождение баланса активных мощностей: P P P P пр ист 100% пр 878,821 878,62 100% 0,023% 0,5% . 878,821 Суммарная реактивная мощность источников: Q ист ~ Im[ S ] Im[878,62 j 29,052] 29,052, ВАР . Суммарная реактивная мощность приемников: Q пр I 12 ( X L1 X C1 ) I 32 ( X L 3 X C 3 ) 2,34 2 (6,16 68,9) 3,939 2 ( 47,94 23,93) 28,993, ВАР Допускается расхождение баланса реактивных мощностей: Q Q Q Q ист пр ист 100% 29,052 28,993 100% 0,2% 0,5% . 29,052 Так как баланс активных и реактивных мощностей сходится, то расчет произведен верно. 4.2.4. Моделирование схемы с помощью программы Electronics Workbench (EWB) Для проверки результатов теоретических расчетов произведем моделирование исследуемой схемы методом физического моделирования. Соберем схему (рис. 4.7) в среде Electronics WorkBench. Снимок с экрана компьютера с показаниями амперметров представлен на рис. 4.9. 19 Рис. 4.9 Как видно из рис. 4.9, показания приборов с небольшой погрешностью совпадают с расчетными значениями. 20