ЛЕКЦИЯ 3 МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ НА ПРИМЕРАХ ЦЕПЕЙ
реклама

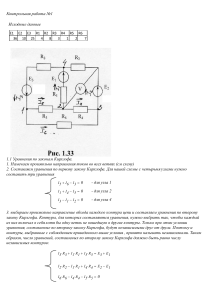
ЛЕКЦИЯ 3 МЕТОДЫ РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ НА ПРИМЕРАХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА Метод расчета цепей с использованием законов Кирхгофа Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемой цепи Пример расчета цепи R1 1к R3 E1 a I1 R4 R2 d I3 I4 E2 R5 b I5 3к UJ I2 2к J c ЗАДАНО: ВСЕ СОПРОТИВЛЕНИЯ, Э.Д.С. И ИСТОЧНИК ТОКА ТРЕБУЕТСЯ: ОПРЕДЕЛИТЬ ТОКИ ВО ВСЕХ ВЕТВЯХ (6 шт.) И ПАДЕНИЕ НАПРЯЖЕНИЯ НА ЭЛЕМЕНТАХ ПОРЯДОК РАСЧЕТА * РАССТАВЛЯЕМ НАПРАВЛЕНИЯ ТОКОВ В ВЕТВЯХ * ОПРЕДЕЛЯЕМ КОЛИЧЕСТВО УЗЛОВ (nУ = 4). Из них количество независимых узлов n= nу-1 * ОПРЕДЕЛЯЕМ КОЛИЧЕСТВО ВЕТВЕЙ (nB = 6) * ОПРЕДЕЛЯЕМ КОЛИЧЕСТВО независимых КОНТУРОВ (К З = nB – nУ + 1= 3) * СОСТАВЛЯЕМ УРАВНЕНИЯ БАЛАНСА ТОКОВ ДЛЯ ЗНАЧИМЫХ УЗЛОВ ПО ПЕРВОМУ ЗАКОНУ КИРХРОФА a: I1 I 4 J 0 b : I3 I4 I5 0 c: I2 I5 J 0 * СОСТАВЛЯЕМ УРАВНЕНИЯ ПО ВТОРОМУ ЗАКОНУ КИРХГОФА ДЛЯ ЗНАЧИМЫХ КОНТУРОВ R1I1 R 3I 3 R 4I 4 E1 2к : R 2I 2 R 3I 3 R 5I 5 E 2 1к : 3к : R 4I 4 R 5I 5 U J Уравнения в матричной форме: a b c 1к 2к 3к I1 I 2 I 3 I 4 I 5 0 0 1 0 1 0 0 1 1 1 1 0 0 1 0 R 0 R R 0 3 4 1 0 R 2 R 3 0 R 5 0 0 R4 R5 0 UJ 0 I1 J I 0 0 2 0 I 3 J 0 I 4 E 1 0 I 5 E 2 1 U J 0 Или: А·Х = В, тогда Х =А-1·В 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 А= R3 R4 0 R1 0 0 R2 R3 0 R5 0 0 R4 R5 0 0 I1 I 0 2 I3 0 Х= В= 0 I4 I 0 5 U J 1 J 0 J E1 E2 0 ТЕОРЕМА ТЕЛЛЕДЖЕНА Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементах рассматриваемой цепи Математическая запись закона ek i k U J q J q u n i n ИЛИ PВ PП Пояснение Эта теорема является законом сохранения энергии в электрической цепи и применяется как баланс мощностей для проверки правильности расчетов Потенциальная диаграмма Потенциальная диаграмма это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми Схема контура E1 к R2 в I1 c I2 E2 R1 а R3 I3 d Потенциалы точек контура: a 0 к а I1R 1 в к Е1 c в I 2 R 2 d c E 2 a d I 3 R 3 0 Потенциальная диаграмма B в в с c R2 R1 R3 a a к d к d R Ом Расчет цепей методом контурных токов В расчет вводятся контурные токи – это фиктивные токи, которые замыкаются в независимых замкнутых контурах, отличающихся друг от друга наличием хотя бы одной новой ветви Например Например : I 22 R1 I1 Е1 a I 44 I3 I11 R2 в R3 Е2 I2 с I 33 I11 , I 22 , I 33 , I 44 контурные токи I1 I11 I 22 I 2 I11 I 44 I 3 I 33 I11 токи ветвей контура По второму закону Кирхгофа: R1I1 R3 I3 R2 I 2 E1 E2 или R1 ( I11 I 22 ) R3 ( I33 I11 ) R2 ( I11 I 44 ) E1 E2 Тогда ( R1 R2 R3 ) I11 R1I 22 R3 I33 R2 I 44 E1 E2 В общем виде Rкк I кк Rкm I mm Eкк Rкк суммарное к-контура I кк контурный ток к-контура сопротивление Rкm общее сопротивление между к-контуром и m -контуром I mm соседний контурный ток m-контура Eкк суммарная ЭДС к-контура Контурный ток рассматриваемого контура умножается на сумму сопротивлений своего контура, причем перед этим произведением ставится знак “+” Соседний контурный ток умножается на общее сопротивление между соседним и рассматриваемым контурными токами, причем перед этим произведением ставится знак “+” если направления этих контурных токов в общем сопротивлении совпадают между собой и ставится знак “-” если направления их не совпадают В правой части уравнения записывается алгебраическая сумма ЭДС рассматриваемого контура, причем со знаком “+” берутся те ЭДС, направления которых совпадают с направлением рассматриваемого контурного тока Для контура с источником тока контурное уравнение не составляется, так как контурный ток этого контура известен и равен току источника тока, причем через источник тока должен проходить только один контурный ток Пример 1 R1 E1 I11 E2 I1 I2 R5 I 33 I5 R3 UJ + J I3 I 22 R4 I4 Контурные уравнения I33 J ( R1 R3 ) I11 R3 I 22 0 I33 E1 E2 R3 I11 ( R5 R3 R4 ) I 22 R5 I33 E2 ( R1 R3 ) ( R3 ) ( R3 ) ( R5 R3 R4 ) I11 I 22 E1 E2 E2 R5 J матрица симметрична относительно главной диагонали I1 I11 I 2 I 22 I 33 I11 I3 I 22 I11 I 4 I 22 I 5 I 22 I 33 по 2 закону Кирхгофа U J R4 I 4 R3 I 3