Тема 7. Анализ линейных электрических цепей
реклама
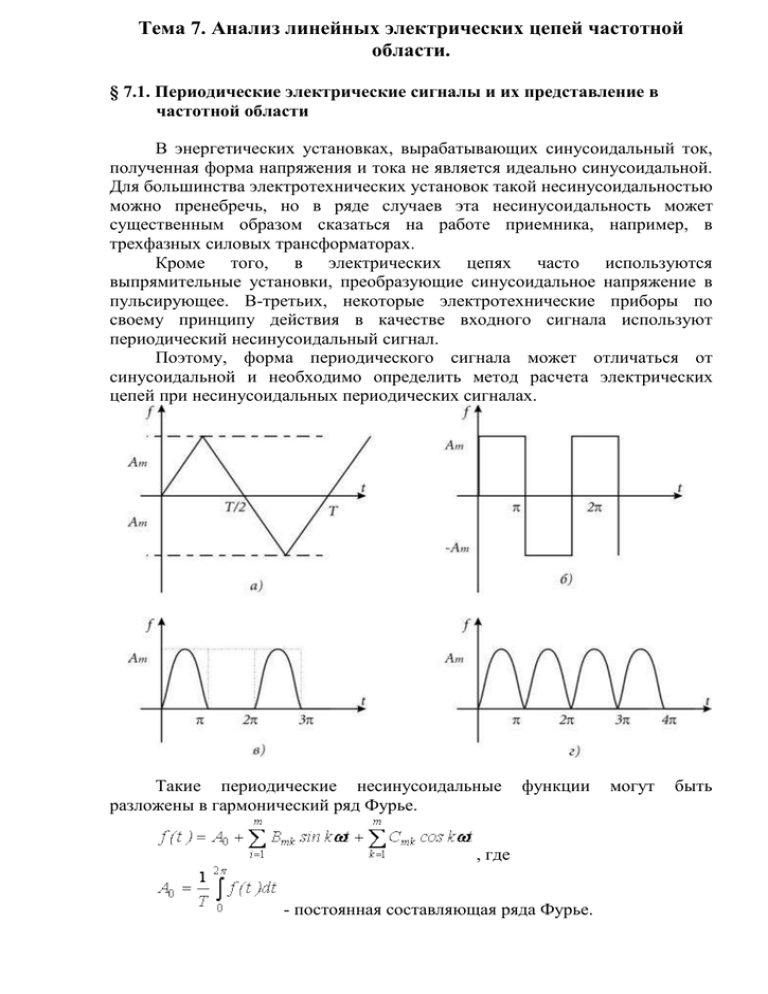
Тема 7. Анализ линейных электрических цепей частотной области. § 7.1. Периодические электрические сигналы и их представление в частотной области В энергетических установках, вырабатывающих синусоидальный ток, полученная форма напряжения и тока не является идеально синусоидальной. Для большинства электротехнических установок такой несинусоидальностью можно пренебречь, но в ряде случаев эта несинусоидальность может существенным образом сказаться на работе приемника, например, в трехфазных силовых трансформаторах. Кроме того, в электрических цепях часто используются выпрямительные установки, преобразующие синусоидальное напряжение в пульсирующее. В-третьих, некоторые электротехнические приборы по своему принципу действия в качестве входного сигнала используют периодический несинусоидальный сигнал. Поэтому, форма периодического сигнала может отличаться от синусоидальной и необходимо определить метод расчета электрических цепей при несинусоидальных периодических сигналах. Такие периодические несинусоидальные разложены в гармонический ряд Фурье. функции , где - постоянная составляющая ряда Фурье. могут быть - гармонические составляющие – гармоники. - основная частота В электротехнике более удобна другая формула: . , - постоянная составляющая. , - первая гармоника. - высшая гармоника. Такое представление позволяет при расчете линейных электрических цепей применять принцип суперпозиции. Считая, сто несинусоидальный сигнал – сигнал от источника, приводят ряд расчетов для каждой составляющей периодического ряда. Полученные при этом результаты складываются. § 7.2. Разложение периодической несинусоидальной функции в ряд Фурье В инженерных задачах используют готовые представления в виде ряда Фурье для типовых периодических функций. Например, а) б) в) г) § 7.3. Действующее значение несинусоидального напряжения и тока (дома) § 7.4. Активная и полная мощность несинусоидального тока (дома) § 7.5. Расчет линейных электрических цепей при несинусоидальных источниках. Если в линейной электрической цепи действует один или несколько несинусоидальных источников, то расчет проводится в 3 этапа: 1) разложение периодической несинусоидальной функции в ряд Фурье. 2) применение принципа наложения и расчет токов и напряжений цепи при действии каждого источника в отдельности. 3) совместное рассмотрение решений, полученных на каждом этапе в отдельности. 1) Обычно используют разложение в ряд Фурье, поскольку с ростом номера гармоники амплитуды синусоид убывают, то достаточно ограничиться тремя-четырьмя гармоническими составляющими. 2) Предположим, что в цепи используется источник напряжения, ЭДС которого изменяется по закону: Допустим, что i(t)-?, тогда сначала строят схему, в которой действует один источник , при закороченных остальных. При построении схемы следует иметь в виду, что цепь не проявляет своих индуктивно-емкостных свойств. Далее, определяется ток при действиях синусоидальной ЭДС . Расчет ведется методом комплексных амплитуд, и по полученной амплитуде записывают полученный ток. . Затем поочередно проводятся расчеты при действии синусоидальных источников: значения токов: , а потом . В результате определяются мгновенные Расчеты производятся методом комплексных амплитуд с одной особенностью, так как частота синусоидального тока с ростом номера гармоники увеличивается, то будут изменяться индуктивные и активные сопротивления элементов электрической цепи: .











