ДЗ-23 (практическая работа по циклам с условиями)

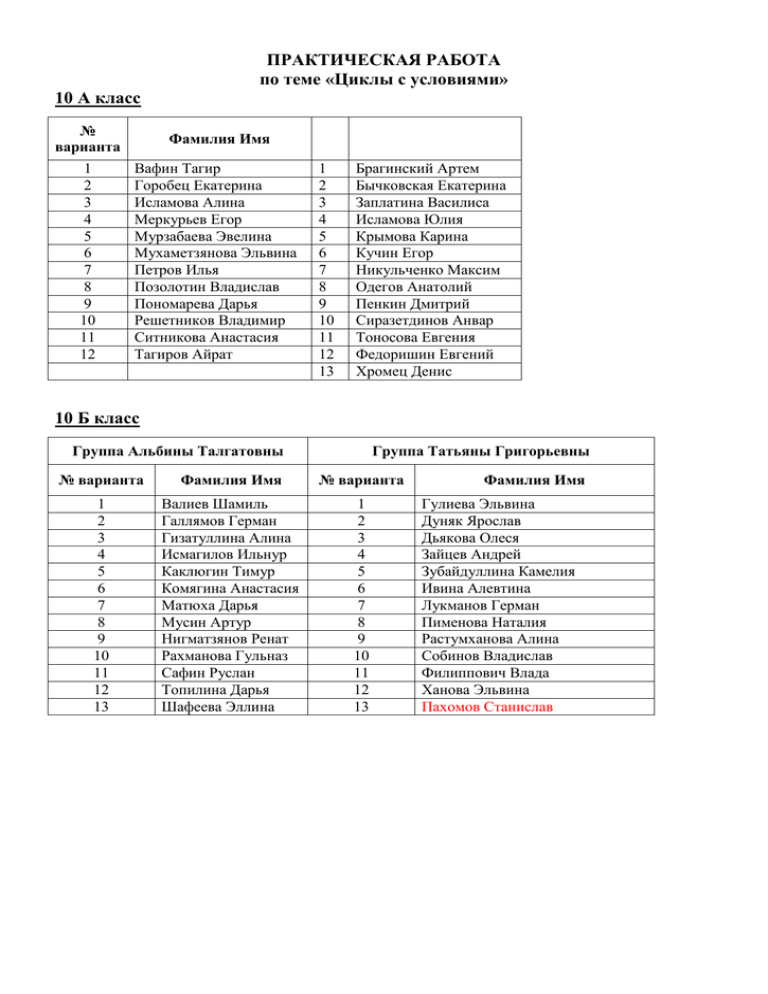
ПРАКТИЧЕСКАЯ РАБОТА
по теме «Циклы с условиями»
10 А класс
№
варианта
Фамилия Имя
1
2
3
4
5
6
7
8
9
10
11
12
Вафин Тагир
Горобец Екатерина
Исламова Алина
Меркурьев Егор
Мурзабаева Эвелина
Мухаметзянова Эльвина
Петров Илья
Позолотин Владислав
Пономарева Дарья
Решетников Владимир
Ситникова Анастасия
Тагиров Айрат
1
2
3
4
5
6
7
8
9
10
11
12
13
Брагинский Артем
Бычковская Екатерина
Заплатина Василиса
Исламова Юлия
Крымова Карина
Кучин Егор
Никульченко Максим
Одегов Анатолий
Пенкин Дмитрий
Сиразетдинов Анвар
Тоносова Евгения
Федоришин Евгений
Хромец Денис
10 Б класс
Группа Альбины Талгатовны
Группа Татьяны Григорьевны
№ варианта
Фамилия Имя
№ варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
Валиев Шамиль
Галлямов Герман
Гизатуллина Алина
Исмагилов Ильнур
Каклюгин Тимур
Комягина Анастасия
Матюха Дарья
Мусин Артур
Нигматзянов Ренат
Рахманова Гульназ
Сафин Руслан
Топилина Дарья
Шафеева Эллина
1
2
3
4
5
6
7
8
9
10
11
12
13
Фамилия Имя
Гулиева Эльвина
Дуняк Ярослав
Дьякова Олеся
Зайцев Андрей
Зубайдуллина Камелия
Ивина Алевтина
Лукманов Герман
Пименова Наталия
Растумханова Алина
Собинов Владислав
Филиппович Влада
Ханова Эльвина
Пахомов Станислав
Вариант 1
1. Даны натуральное число N, действительное число X. Вычислить:
2. Даны
n

i:1
натуральное
число
N,
действительное
число
X.
k  sin k x

k
k 1 tg ( x  2)
n
Вычислить:
x  sin ( x  2)
i  i!
i
i
3. Дано натуральное число n. Поменять местами первую и последнюю цифры
этого числа.
4. Напишите программу перевода числа из двоичной системы счисления в
четверичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x2 x4 x6
   ... , где х<1.
2
4
6
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 2
1. Даны натуральное число N, действительное число X. Вычислить:
k  cos k x

k
k 1 ctg ( x  k )
n
2. Даны натуральное число N, действительное число X. Вычислить:
n
i  cos i x

i
i:1 cos( x )  i!
3. Дано натуральное число n. Найти сумму первой и последней цифры этого
числа.
4. Напишите программу перевода числа из двоичной системы счисления в
восьмеричную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x3 x5
x    ... , где х<1.
3
5
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.001.
Вариант 3
k  tg k x
1. Даны натуральное число N, действительное число X. Вычислить: 
k
k 1 sin( x )
n
2. Даны
n

i:1
натуральное
число
N,
действительное
число
X.
Вычислить:
cos ( x)  tg ( x )
i!
i
i
3. Дано натуральное число n. Проверьте есть ли в записи числа три одинаковые
цифры.
4. Напишите программу перевода числа из двоичной системы счисления в
шестнадцатеричную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x3 x6 x9
   ... , где х<1.
3
6
9
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 4
1. Даны натуральное число N, действительное число X. Вычислить:
2. Даны
натуральное
число
N,
действительное
число
X.
k  sin k x

k
k 1 ctg ( x )
n
Вычислить:
 i tg i ( x) 

 x  i! 
i 1 

n
3. Дано натуральное число n. Дописать цифру k в начало и конец этого числа.
Например, дано n=123, k=8, получить 81238.
4. Напишите программу перевода числа из четверичной системы счисления в
двоичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x  1 ( x  1) 2 ( x  1)3


 ... , где х>0,5.
x
2x2
3x 3
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 5
1. Даны натуральное число N, действительное число X. Вычислить:
2. Даны
натуральное
число
N,
действительное
число
X.
k  tg k x

k
k 1 sin( x  2)
n
Вычислить:
 k!

k
 k  ctg x 


k 1  2
n
3. Дано натуральное число n. Найти максимальную и минимальную цифры этого
числа.
4. Напишите программу перевода числа из восьмеричной системы счисления в
двоичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
1
1
1
 3  5  ... , где х>1.
x 3x
5x
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 6
1. Даны натуральное число N, действительное число X. Вычислить:
2. Даны
натуральное
число
N,
действительное
число
X.
k  sin k x

k
k 1 tg ( x  2)
n
Вычислить:
 k! x
k 

tg
x
xk

k 1
n
 
3. Даны натуральные числа n и k. Определить сколько раз встречается в записи
числа n цифра k.
4. Напишите программу перевода числа из шестнадцатеричной системы
счисления в двоичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
( x  1) 2 ( x  1) 4 ( x  1) 6


 ... , где х<0,5.
2
4
6
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 7
1. Даны натуральное число N и действительное число X. Вычислить:
k  cos k x

k
k 1 ctg ( x  k )
n
2. Даны
натуральное
число
N,
действительное
число
X.
Вычислить:
 k!ctg ( x k ) 



k
sin x 
k 1 
n
3. Дано натуральное число n. Заменить нечетные цифры в записи данного числа
на цифру 2. Например, дано число 3467, получить 2462.
4. Напишите программу перевода числа из десятичной системы счисления в
четверичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x 4 x 8 x12
 
 ... , где х<1.
1
2
3
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 8
1. Даны натуральное число N и действительное число X. Вычислить:
k  tg k x

k
k 1 sin( x  1)
2. Даны
Вычислить:
натуральное
число
N,
действительное
число
X.
n
 k! sin( x k ) 



k
tg
x
k 1 

n
3. Дано натуральное число n. Найти произведение четных цифр данного числа.
4. Напишите программу перевода числа из десятичной системы счисления в
двоичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x  1 ( x  1) 2 ( x  1) 3


... , где х<1.
2
4
6
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.001.
Вариант 9
1. Даны натуральное число N и действительное число X. Вычислить:
k  sin k x

k
k 1 ctg ( x )
2. Даны
Вычислить:
натуральное
число
N,
действительное
число
X.
n
 x  ctg ( x k ) 



k
k
!

sin
x
k 1 

n
3. Дано натуральное число n. Заменить четные цифры в записи данного числа на
цифру 1. Например, дано число 3467, получить 3117.
4. Напишите программу перевода числа из десятичной системы счисления в
восьмеричную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x2 x4 x6
   ... , где х<1.
1
3
5
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 10
1. Даны натуральное число N и действительное число X. Вычислить:
k  tg k x

k
k 1 sin( x  2)
2. Даны
Вычислить:
натуральное
число
N,
действительное
число
X.
n
 x  sin( x k ) 



k
k
!

tg
x
k 1 

n
3. Дано натуральное число n. Найти сумму четных цифр в записи данного числа.
Например, дано число 3467, получить 20.
4. Напишите программу перевода числа из десятичной системы счисления в
восьмеричную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
2! 4!
6!
 2  3  ... , где х>0,5.
x 2x
3x
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 11
1. Даны натуральное число N и действительное число X. Вычислить:
k  sin k x

k
k 1 tg ( x  2)
2. Даны
Вычислить:
натуральное
число
N,
действительное
число
X.
n

ctg ( x k ) 



x 

k
!
k 1 

n
3. Дано натуральное число n. Записать число в обратном порядке. Например,
дано число 3467, получить 7643.
4. Напишите программу перевода числа из восьмеричной системы счисления в
десятичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
1!
3!
5
 2  3  ... , где х>1.
2x 4x
6x
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 12
1. Даны натуральное число N и действительное число X. Вычислить:
k  cos k x

k
k 1 ctg ( x  k )
n
2. Даны
натуральное
число
N,
действительное
число
X.
Вычислить:
 k tg ( x k ) 
 x 


x

k
!
k 1 

n
3. Дано натуральное число n>1000. Получить новое число, удалив из данного
числа четные цифры. Например, дано число 123456, получить 135.
4. Напишите программу перевода числа из восьмеричной системы счисления в
десятичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x 5 x10 x15


 ... , где х>0,5.
1! 2!
3!
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.
Вариант 13
1. Даны натуральное число N и действительное число X. Вычислить:
k  tg k x

k
k 1 sin( x )
2. Даны
Вычислить:
натуральное
число
N,
действительное
число
X.
n
 k
sin( x k ) 
 x 


k
cos
x

k
!
k 1 

n
3. Дано натуральное число n>1000. Получить новое число, удалив из данного
числа нечетные цифры. Например, дано число 123456, получить 246.
4. Напишите программу перевода числа из четверичной системы счисления в
десятичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
3!
6!
9!
 6  9 ... , где х<1.
3
x
2x
3x
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.001.
Вариант 14
k  sin k x
1. Даны натуральное число N и действительное число X. Вычислить: 
k
k 1 ctg ( x )
n
2. Даны
натуральное
число
N,
действительное
число
X.
Вычислить:
 ctg ( x k ) 



k
k 1  cos x  k! 
n
3. Дано натуральное число n>1000. Получить новое число, удалив из данного
числа цифры кратные трем. Например, дано число 123456, получить 1245.
4. Напишите программу перевода числа из двоичной системы счисления в
десятичную.
5. Дано действительное число Х. Вычислить приближенное значение
бесконечной суммы с заданной точностью:
x x3 x5
   ... , где х<1.
3 6
9
Нужное приближение считается достигнутым, если вычислена сумма нескольких
слагаемых, и очередное слагаемое оказалось по модулю меньше заданного числа
=0.0001.