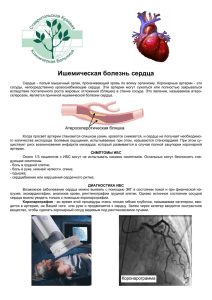
Динамическая модель ауторегуляции кровотока в тонкостенной
реклама

УДК 51(06) Проблемы современной математики Н.А. КУДРЯШОВ, И.Л. ЧЕРНЯВСКИЙ Московский инженерно-физический институт (государственный университет) ДИНАМИЧЕСКАЯ МОДЕЛЬ АУТОРЕГУЛЯЦИИ КРОВОТОКА В ТОНКОСТЕННОЙ АРТЕРИИ Построена математическая модель для процесса ауторегуляции кровотока в тонкостенной артерии при установившемся течении с заданным профилем скоростей. Учтены кинетические процессы, описывающие производство оксида азота и действие кальциевых насосов в стенке артерии. Принята во внимание нелинейная упругость и вязкость кровеносного сосуда. Проведен анализ устойчивости стационарных решений данной динамической системы. На фазовой диаграмме, вблизи точек покоя изучено влияние различных биомеханических факторов на процесс локальной ауторегуляции. Как правило, при описании течения крови в артерии используется приближение пассивного сосуда, что по существу эквивалентно анализу течения жидкости в вязкоэластичной трубке. Однако для реально происходящих процессов характерна обратная связь, которая возникает при учете зависимости концентрации оксида азота (NO), образующегося в эндотелиальном слое стенки артерии от вязкого сдвигового напряжения на ее внутренней поверхности, и последующей реакции сосудистых гладких мышц [1, 2]. В работе [2] обсуждается возможность продуцирования в эндотелии и других агентов в ответ на механическое действие кровотока. В данной модели в качестве сигнальной молекулы учитывается оксид азота. Рассматриваемая в работе модель является развитием ранее предложенной двухслойной диффузионно-кинетической модели [3]. Для описания процесса авторегуляции в тонкостенной артерии используется динамическая система уравнений в виде: где n(t) - концентрация оксида азота в стенке артерии, x(t) - усредненная по объему стенки концентрация ионов кальция в гладкомышечном слое, ISBN 5-7262-0710-6. НАУЧНАЯ СЕССИЯ МИФИ-2007. Том 7 103 УДК 51(06) Проблемы современной математики y(t) = (R(t)-R0)/R0 - относительное отклонение радиуса артерии от равновесного, z(t) - скорость осцилляций радиуса сосуда. Первое уравнение описывает кинетику NO, интенсивность производства которого в эндотелии предполагается пропорциональной величине сдвигового напряжения. Второе уравнение отвечает за баланс ионов кальция в гладкомышечном слое, в предположении соответствия работы кальциевых насосов обобщенному закону Михаэлис-Ментен. Последнее уравнение описывает колебания радиуса с учетом активного напряжения стенки артерии, а также с учетом вязкости и нелинейной упругости материала стенки [4]. Данная система имеет стационарную точку, отвечающую отсутствию колебаний радиуса артерии при выполнении условия баланса между мышечными силами и силами давления, которое в случае s = 1 принимает вид: Численное моделирование поведения системы вблизи точек покоя позволило выделить различные режимы ауторегуляции. Показано, что величина вязкости стенки сосуда влияет на ее устойчивое равновесие, определяет предельный цикл или приводит к сложным осцилляциям радиуса артерии. Результаты решения задачи [5] сравнивались с экспериментальными данными [2]. Список литературы 1. Регирер С.А., Шадрина Н.Х. Элементарная модель сосуда со стенкой, чувствительной к механическим стимулам // Биофизика, 2002. Т. 47, № 5. С. 908-913. 2. Мелкумянц А.М., Балашов С.А. Механочувствительность артериального эндотелия. Тверь:Триада, 2005. 208 с. 3. Кудряшов Н.А., Чернявский И.Л. Модель ауторегуляции течения крови в артерии с учетом эндотелий-зависимого фактора - оксида азота // Научная сессия МИФИ-2006: Сб. науч. тр.: В 16 т. М.:МИФИ, 2006. Т. 7. С. 116-117. 4. Zhou J., Fung Y.C. The degree of nonlinearity and anisotropy of blood vessel elasticity // Proc. Natl. Acad. Sci. USA, 1997, v. 94, pp. 14255-14260. 5. Кудряшов Н.А., Чернявский И.Л. Численное моделирование процесса ауторегуляции потока крови в артерии // IX Всероссийский Съезд по Теоретической и Прикладной Механике, 2006. Т. 1. С. 150-151. ISBN 5-7262-0710-6. НАУЧНАЯ СЕССИЯ МИФИ-2007. Том 7 104