МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ НОМОГРАММ В ЭКСТРЕМАЛЬНОЙ МЕДИЦИНЕ. Соловкина Юлия Владимировна
реклама

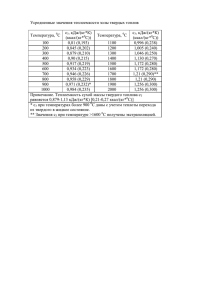
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ НОМОГРАММ В ЭКСТРЕМАЛЬНОЙ МЕДИЦИНЕ. Соловкина Юлия Владимировна Научный руководитель ─ учитель математики Мячкина Эльвира Алексеевна Русская классическая гимназия №2, г. Томск г.Томск, ул. Лебедева, 92. ПЛАН 1. Понятие о номографии. 2. Номограмма переносимости низких температур в зависимости от теплоизолирующих свойств одежды. 3. Расчет времени переносимости человеком холода в одежде с различной теплоизоляцией при разнообразных условиях и физической нагрузке. 4. Математическое моделирование вопросов выживания человека в холодной воде. 5. Заключение. 6. Используемая литература. 1. ПОНЯТИЕ О НОМОГРАФИИ На производстве, в технике, медицине, в военном деле при вычислениях массового характера широко применяются номограммы специальные чертежи, дающие возможность быстро получать готовые результаты сложных вычислений. Номография - часть математики, которая устанавливает способы построения и использования номограмм - позволяет производить математическое моделирование различных видов деятельности человека. Творцом общей теории номограмм является французский математик Морис Окань (1862 – 1932), опубликовавший ряд работ по теории «считающих чертежей». Он и назвал их «номограммами» (от греческого номос - закон, грамма – запись). Основную роль в построении номограмм играет градуирование шкал. С помощью номограмм можно быстро выполнить расчеты, которые позволяют осуществить контроль различных производственных процессов, принять правильные управленческие решения в экстремальных ситуациях, помогают ускорить постановку диагноза заболеваний человека, определить возможный исход поражений при воздействии неблагоприятных факторов среды на организм. Математическое моделирование с помощью номограмм в медицине, в том числе и экстремальной, осуществляется по следующей схеме: 1. Выявляется математическое правило, на основании которого строится номограмма – формула или таблица, с помощью которой задана некоторая определенная функция; 2. Устанавливается область определения функции; 3. Отбираются значения параметра, для которых строятся графики функции; 4. Строится график функции для каждого значения параметра. Я решила изучить применение данной схемы в медицинской практике, рассмотрев построение номограмм при изучении вопросов выживания человека в экстремальных ситуациях, связанных с воздействием на организм низких температур. 2. НОМОГРАММА ПЕРЕНОСИМОСТИ НИЗКИХ ТЕМПЕРАТУР В ЗАВИСИМОСТИ ОТ ТЕПЛОИЗОЛИРУЮЩИХ СВОЙСТВ ОДЕЖДЫ Где бы ни оказались люди, терпящие бедствия, - среди льдов Центрального полярного бассейна или в заснеженной тундре, - главным их врагом с первых же минут становится холод. Борьба с холодом, с воздействием на организм низких температур - важнейшая проблема автономного существования человека, особенно зимой. Очевидно, что большое значение в предупреждении поражений холодом будет играть одежда, которая для пребывания на морозе должна обладать низкой теплопроводностью и высокой воздухопроницаемостью. Существует прямая зависимость времени, в течение которого организм человека сохраняет тепловой комфорт, от величины температуры окружающей среды и теплоизолирующих свойств одежды. Эта зависимость иллюстрируется номограммой (рис. 1). На графике А, данной номограммы видно, что человек, одетый в летний комбинезон, при температуре минус 5˚ будет испытывать тепловой комфорт не более получаса. Столько же времени пройдет, если его одеть в шерстяное белье и ватную куртку при наружной температуре воздуха минус 30˚ (Б) или комплект, состоящий из шерстяного белья, свитера и меховой куртки с брюками при температуре минус 50˚ (В). А если добавить к меховой куртке подстежку (Г), человек начнет мерзнуть через 45-60 минут. Номограмма американского ученого С. Лутц показывает, что рано или поздно теплопотери окажутся больше, чем теплопродукция, и начнется охлаждение организма. Процесс этот начинает быстро развиваться при температуре -12˚. Мною был проведен опыт, доказывающий что эта номограмма действительно верна: несколько человек, одетых в летнюю одежду при температуре минус 5˚ вышли на улицу. Большинство из них испытывало тепловой комфорт около 20-25 минут, и лишь два человека смогли испытывать тепловой комфорт 25-30 минут. При температуре минус 30˚ люди, одетые в теплую ватную куртку, шерстяные свитера, ватные брюки испытывали тепловой комфорт в течение 20-25 минут. К сожалению, опыт при температуре минус 50˚ мне провести не удалось. Но проведенные мной опыты доказали, что номограмма составлена верно. 3. РАСЧЕТ ВРЕМЕНИ ПЕРЕНОСИМОСТИ ЧЕЛОВЕКОМ ХОЛОДА В ОДЕЖДЕ С РАЗЛИЧНОЙ ТЕПЛОПРОВОДНОСТЬЮ ПРИ РАЗНООБРАЗНЫХ УСЛОВИЯХ И ФИЗИЧЕСКОЙ НАГРУЗКЕ Российские ученые В.И Кричагин, В.И. Хроленко и А.И Резников составили специальную номограмму для расчетов ориентировочного времени переносимости человеком холода в одежде с различной теплоизоляцией при разнообразных условиях и физической нагрузке. В основу номограммы была положена формула: Q= S (33 t s ) , где Q - тепловой поток со всей поверхности тела (S-1,6 I факт . кв.м) (в ккал/час) : I - фактическая теплоизоляция одежды в единицах «кло». Кло - единица теплоизоляции, равная 0,18 град/м 2 /час, обеспечивающая состояние комфорта у человека, находящегося в состоянии покоя, при теплообразовании 50ккал/м 2 /час; t s - температура окружающего воздуха. Вторая (нижняя) часть номограммы позволяет вычислить дефицит тепла в организме по формуле Д = Q – M, где Д - дефицит тепла в организме (Д, равное 80 ккал/час, соответствует переходу в состояние дискомфорта II степени, а Д, равное 180 ккал/час - III степени; Q - общие теплопотери (в ккал/час) организма, определяемые по верхней части номограммы; Mтеплопродукция организма (в ккал/час). Пользуясь этой номограммой, можно решать любые задачи по прогнозированию допустимых интервалов времени пребывания человека на холоде. Выбранная величина теплоизоляции одежды откладывается на шкале I факт . На этом уровне проводится горизонталь до пересечения с линией, обозначающей заданную температуру воздуха. Из этой точки опускается перпендикуляр до дугообразной линии, которая имеет соответствующие обозначение уровня физической нагрузки (в ккал/час); из последней точки проводится горизонталь до пересечения с правой или левой шкалой, где указано время наступления дискомфорта II или III степеней, при которых создается угроза трудоспособности человека. Если числовые значения энерготрат находятся правее вертикали, проведенной от первой точки пересечения в нижнюю половину номограмм, то это значит, что теплозатрата через данную одежду недостаточна и организм будет перегреваться. Таким образом, по номограмме можно получать и количественную характеристику перегревания организма. 4. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВОПРОСОВ ВЫЖИВАНИЯ ЧЕЛОВЕКА В ХОЛОДНОЙ ВОДЕ Математическое моделирование вопросов выживания человека в холодной воде является чрезвычайно важной задачей и прежде всего для организации и проведения спасательных и медицинских мероприятий. Известно, что даже в тропиках, где температура океанской воды относительно высока, время пребывания в ней человека ограничено, поскольку она все-таки ниже температуры тела. В результате организм непрерывно теряет тепло и температура тела, постепенно снижаясь, рано или поздно достигает критического предела, при котором невозможна жизнедеятельность организма и его систем. И это не случайно, ведь теплопроводность воды в 27 раз больше, чем воздуха. При температуре воды 22˚ человек за 4 минуты теряет 100 ккал, т.е. примерно столько же, сколько на воздухе при той же температуре за час. Известно, что в апреле 1912 года при гибели «Титаника» от столкновения с айсбергом, спасательные суда, приняв сигнал бедствия, прибыли на место катастрофы всего через 1 час 50 минут. Они подняли на борт людей, находившихся в шлюпках. Но ни одного из 1489 пассажиров оказавшихся в воде, спасти не удалось. Американские ученые Г. Смит и Е. Хэме составили номограмму для расчета времени выживания в холодной воде. Номограмма учитывает характер одежды, теплообразование, вес человека и, наконец, площадь тела, погруженного в воду. В примере, обозначенном мной в номограмме сплошной линией, человек, имеющий теплоизоляцию, равную Н = 0.30 кло, находящийся в воде с t = 4˚ теряет 610 ккал/кв.м /час. Теплопродукция составляет тепла М , 400 ккал/кв.м/час, дефицит А Д - 210 ккал/кв.м/час; площадь тела, погружаемого в воду - 1,75 кв.м. А Уменьшение теплосодержания организма в час должно составлять 365-400 ккал/час. При весе 75 кг (В) температура тела будет падать в час на 6˚. Если за предельно низкую температуру Тула принять 31˚, то человек может находиться в воде при 4˚ в течение 1 часа. 5. ЗАКЛЮЧЕНИЕ Из выше разобранных мной номограмм, можно сделать вывод, что математическое моделирование с помощью номограмм может быть широко использовано для выполнения практических расчетов в различных областях медицины, а также при конструировании и испытании одежды для работы в условиях низких или высоких температур. 6. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА 1. Волович В.Г. Человек в экстремальных условиях природной среды. – М., Мысль, 1990. 2. Волович В.Г., Бычков О.К., Усков В.Н. Некоторые вопросы работоспособности и жизнедеятельности человека при автономном существовании в условиях низких температур. – Фрунзе, Илим, 1987. 3. Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. – М., Просвещение, 1998.