1.09 Изучение прецессии гироскопа.

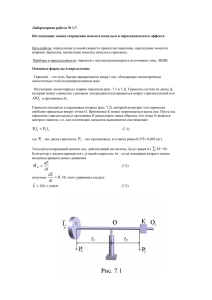
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ «МАМИ»
Кафедра
физики
ЛАБОРАТОРНАЯ РАБОТА 1.09
ИЗУЧЕНИЕ ПРЕЦЕССИИ ГИРОСКОПА
Москва
2005 г.
Лабораторная работа N 109
ИЗУЧЕНИЕ ПРЕЦЕССИИ ГИРОСКОПА
Цель работы: Определение угловой скорости прецессии и момента инерции гироскопа
ВВЕДЕНИЕ
Гироскопом или волчком называется массивное симметричное тело.
вращающееся с большой скоростью вокруг оси симметрии. На рис.1
изображен
гироскоп,
вращающийся с угловой
скоростью ω вокруг

вертикальной
оси симметрии. Угловая скорость ω и момент импульса гирос

копа L  Jω направлены вертикально вверх вдоль оси симметрии.
Одно из свойств гироскопа – способность сохранять неизменным
направление оси вращения
 в пространстве при отсутствии
момента внешних сил M , что следует из закона сохранения

момента импульса: Jω  const , если M  0 .
Другое свойство гироскопа состоит в том, что при
кратковременном воздействии на ось гироскопа она сохраняет
свое направление в пространстве. Действительно, из
основного закона динамики вращательного движения

 d Jω
M
dt


или MΔt  ΔJω

следует, что если момент внешних сил M действует в течение
короткого времени Δt  0 , то изменение момента импульса

гироскопа (ΔJω  0) стремится к нулю, и ось гироскопа сохраняет свое направление в пространстве.
Если момент внешних сил, действующих на
гироскоп,
не равен нулю и не действует
кратковременно, ось гироскопа начинает поворачиваться
в пространстве.
Движение оси
гироскопа под действием момента внешних сил
называется прецессией.
На гироскоп,
изображенный
на рис. 2,



действует момент силы тяжести M  [ r  mg] , где

r – радиус-вектор, проведенный из точки О в точку
приложения силы тяжести mg . Под действием
момента силы тяжести гироскоп совершает прецессию: его ось описывает в пространстве конус.
Угловая скорость прецессии равна
Ω
d
dt
(1)
2
где d – угол поворота оси гироскопа за время dt .
ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ
Упрощенная схема гироскопа,
работе, представлена на рис. 3
используемого в данной лабораторной
Гироскоп имеет одну точку опоры O . Если центр масс системы совпадает
с точкой опоры, гироскоп является уравновешенным.
Если к оси

уравновешенного гироскопа приложена сила F , направленная
вертикально,

 

вниз, момент этой силы относительно точки О равен M  [ r  F] , где r –
радиус–вектор, проведенный из точки О в точку приложения силы.
Момент силы в этом случае направлен вдоль оси х, то есть

перпендикулярно силе, и по модулю равен M  r  F (угол между r и F равен
x
90 градусов).


M
Δt

Δ
L
Из основного закона динамики вращательного
движения


следует, что изменение момента импульса ΔL параллельно вектору M .
Следовательно

через момент времени Δt момент импульса гироскопа станет
равным L  ΔL , и осъ гироскопа изменит свое положение в пространстве,
повернувшись на угол Δ в горизонтальной плоскости вокруг оси z. При этом

момента силы M в новом положении снова перпендикулярен
оси гироскопа.

Снова произойдет изменение момента импульса L и т.д. В результате ось
гироскопа под действием момента внешних сил будет непрерывно вращаться в
горизонтальной плоскости с некоторой угловой скоростью Ω , т.е. будет
наблюдаться прецессия.
3
d
. Из рис. 3 видно, что при
dt
ΔL
малых углах поворота оси гироскопа Δ 
.
Следовательно:
L
d L Mt M
M
Ω



то есть Ω 
(2)
dt Lt Jωt Iω
Jω
В данной работе сила F создается путем смещения груза 2 (рис. 4) из
равновесного положения а на расстояние l в точку б.
Найдем угловую скорость прецессии Ω 
2
На ось гироскопа действуют моменты силы тяжести гироскопа и груза. В
положении равновесия их векторная сумма равна
(3).
mГgl1  mg l2  0
где l1 – расстояние от точки О до центра инерции гироскопа. l2 – расстояние от
точки О до центра инерции груза. mГ – масса гироскопа, m - масса груза.
После смещения груза вправо на расстояние l суммарный момент сил
относительно точки О будет равен
M  mg( l2  l )  mГ gl1
M  mg l
С учетом (3) имеем
(4)
Подставляя момент силы из (4) в формулу (2) получаем формулу для
угловой скорости прецессии
Ω
mg l
,
Iω
(5)
где m – масса груза, l – расстояние, на которое смещают груз, I – момент
инерции гироскопа относительно горизонтальной оси симметрии, ω - угловая
скорость вращения гироскопа.
В данной работе экспериментально определяют угловую скорость
прецессии по формуле
Ω

t
(6)
4
Определив  и пользуясь формулой (5), получим формулу для
определения момента инерции гироскопа относительно оси симметрии.
I
mg l
Ωω
(7)
ОПИСАНИЕ УСТАНОВКИ
Общий вид установки показан на рис. 5.
Массивный маховик 1 (гироскоп)
может
вращаться
вокруг
горизонтальной оси.
Вращение
маховика осуществляется электродвигателем 2. Скорость вращения
маховика
может плавно изменяться от 0 до 6000 об/мин. Рычаг 3,
закрепленный на
корпусе
двигателя,
имеет
нанесенную
метрическую шкалу. На рычаге
расположен груз 4, при помощи
которого
можно
уравновесить
гироскоп.
На лицевой панели прибора
находится: указатель скорости вращения
электродвигателя
5,
регулятор
скорости
вращения
электродвигателя 6. цифровое табло
угла поворота 7 и времени
вращения 8.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Нажать клавишу «сеть».
2. При помощи перемещаемого груза установить рычаг гироскопа
горизонтально (уравновесить гироскоп).
3. Ручкой «регулятор скорости» включить питание электродвигателя.
Отрегулировать обороты двигателя примерно на 4000 об/мин и
поддерживать ее постоянной во время эксперимента. Записать число
оборотов n в таблицу.
4. Переместить груз примерно на 4 см влево или вправо. Измерить
смещение груза l - результаты измерений занести в таблицу.
5. Нажать клавишу «сброс».
5
6. Нажать клавишу «стоп» после того как ось гироскопа повернется на 50°100° (на табло 7 высвечиваются цифры 5-10). Значение угла поворота  и
времени поворота t занести в таблицу 1.
7. Повторить измерения не менее 3 раз. Все экспериментальные результаты
занести в таблицу 1.
Таблица 1.
m  Δm 
l

n
t
Ω  ΔΩ 
I  ΔI 
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1. Вычислить угловую скорость прецессии по формуле
Ω

t
2. Вычислить момент инерции гироскопа по формуле
mg l
mg l

Ωω Ω  2π  n
3. Рассчитать относительные ошибки ε Ω и ε I по формулам
I
εΩ 
ΔΩ Δ Δt
;


Ω

t
εI 
Δm Δl ΔΩ Δn



m
l
Ω
n
4. Рассчитать абсолютные ошибки ΔΩ и ΔI по формулам
ΔΩ  Ω  ε Ω , ΔI  ε I  I
5. Окончательные результаты записать в виде
Ω  Ω  ΔΩ
I  I  ΔI
6
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется гироскопом?
2. Сформулируйте основной закон динамики вращательного движения.
3. Что называется моментом силы и как определяется его направление?
4. Сформулируйте закон сохранения момента импульса.
5. Что называется угловой скоростью и как определяется ее направление?
6. Выведите формулу для угловой скорости прецессии (2).
7. От чего зависит угловая скорость прецессии гироскопа?
ЛИТЕРАТУРА
1.
Детлаф А.А., Яворский Б.М. Курс физики. М.: «Высшая школа».1999 г.
2.
Трофимова Т.И. Курс физики. М.: «Высшая школа». 2003г.
3.
Савельев И.В. Курс общей физики. М.: «Наука».2001 г. Книги 1,4.
4.
Сивухин Д.В. Общий курс физики. М.: «Наука».2003. Т.I.