Некоторые практические задачи, приводящие к

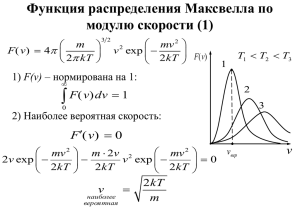
Некоторые практические задачи, приводящие к
дифференциальным уравнениям.
1 .Прохождение  - квантов через вещество
К  - излучению относят электромагнитные волны, длина которых
значительно меньше межатомных расстояний:    , где  имеет порядок
108 см..
В корпускулярной картине это излучение представляет собой поток
частиц, называемых  - квантами.
При прохождении  - квантов через вещество их энергия не меняется (т. е.
частота и длина волны остаются неизменными), но в результате столкновений с
частицами среды постепенно ослабляется интенсивность падающего пучка  квантов. Нетрудно получить закон, по которому происходит это ослабление.
Обозначим через  монохроматический поток падающих частиц, т. е. число
частиц, проходящих через 1 см в 1 с. Пройдя слой вещества толщиной dx, пучок
2
ослабнет на величину d  . Очевидно, что d  , пропорционально потоку и толщине
слоя:
dI   Idx.
Если среда однородна, то коэффициент  постоянен. В этом случае полученное
дифференциальное уравнение легко интегрируется:
I  Ce x
Значение константы С можно определить из условия : С=  0 где  0 - начальная
интенсивность. Заметим, что величина  называется коэффициентом поглощения,
свойства среды по отношению к поглощению

- квантов характеризует полностью
и известна для большого количества веществ, в том числе и для используемых в
строительстве. Очевидно, что для защиты от  - излучения выгодны фильтры с
большими значениями  , однако при этом надо учитывать, что, вообще говоря,
   ( ), хотя на вид полученного дифференциального уравнение и его решения это
обстоятельство не влияет.
2. Хиральность биологических молекул.
Подавляющее большинство сколько-нибудь сложных молекул, содержащих
более чем три атома, не имеет плоскости и центра симметрии. Такие молекулы
дисимметричны, хиральны. Термин «хиральность» (от греческого «хейр» -рука)
означает несовпадение некоторой структуры с её зеркальным отражением.
Хиральные вещества могут фигурировать в двух формах: правой и левой. Эти две
конфигурации нельзя совместить друг с другом никаким поворотом в
пространстве – как правую и левую руки. В мире молекул чаще всего хиральность
обусловлена наличием так называемого асимметрического атома углерода. Атом
углерода становится асимметрическим, если все четыре группы, с которыми он
связан, различаются. Такая молекула не имеет ни плоскости, ни центра симметрии.
В химическом синтезе из исходных симметрических молекул вещество всегда
получается в виде рацемической смеси, содержащей 50 % правого (D) и левого (L)
антипода. Удивительным свойством живой природы является фиксация в
организмах всех важнейших биологических молекул, начиная с аминокислот, в
одной определённой конфигурации. Например, все аминокислотные остатки в
белках всегда являются «левыми», L-формами. Как такое могла осуществить
природа в условиях изотропного пространства, при условии, что D - и L- формы
одинаково реагируют с симметричными молекулами? Для разделения антиподов
необходимо асимметрическое воздействие вещества или существа, знающего
разницу между правым и левым. Такое утверждение открывает обширное поле для
гипотез различного свойства. Однако можно показать, что если система является
автокаталитической ( типа РНК), то рано или поздно левая или правая форма
станет доминирующей. Покажем это. Пусть X 1 и X 2 - числа молекул полимера (
типа РНК), построенного естественно на D – и L –мономеров, количества которых
мы обозначим через M1 и M2 , а концентрация- через m1 и m2. Полимеры строят
свои копии из мономеров – имеется матричная авторепродукция. Кроме того,
полимеры способны распадаться. Кинетические уравнения, описывающие развитие
системы имеют вид (а)
dx1
 ax1w1  bx1 ,
dt
dx2
 ax2 w2  bx2
dt
(
Где а и b-константы скоростей полимеризации и распада.
w1 
m1
,
m1  m 2
w2 
m2
,
m1  m 2
w1  w2  1
Это вероятности встречи матриц 1 и 2 с мономерами D и L соответственно. В
стационарном состоянии
dx1 dx2

 0,
dt
dt
w1  w2 
b
a,
Откуда
И, значит, m1  m2 , т е w1  w2  0,5 a  2b и система рецемична. Нетривиальное
развитие системы возможно при неравенстве m1  m2 в результате флуктуации.
Допустим, что
w1  0,5   ;
w2  0,5  
Причем   const  0 (причины такого отклонения могут быть любыми). Тогда
решение системы(а) имеет вид
x1  x1 (0) exp[( a \ 2  b)t ] exp( at ),
x 2  x 2 (0) exp[ a / 2  b)t ] exp( at )
Рекомендуется провести все выкладки самостоятельно, рационально применить
метод разделения переменных. С течением времени популяция D станет
доминирующей:
x1 x1 (0)

exp( 2at ).
x2 x2 (0)
Последующая биологическая эволюция означает дальнейшее закрепление
хиральности, т. к. хиральные системы, отличая правое от левого, более специфично
взаимодействует с окружающей средой, чем рацемичесние.
3 . Люминесценция.
Спектры люминесценции сложных молекул обычно оказываются размытыми,
поэтому информацию о свойствах вещества несут в основном интенсивность,
поляризация и длительность свечения.
Допустим, что в t=0 имеется n(0) возбудённых молекул. Если вероятность перехода
за 1 с из возбуждённого состояния в невозбуждённое с излучение кванта света есть
f , а вероятность безызлучательного перехода есть g, то
dn  ( f  g )ndt
n(t )  n(0) exp[ ( f  g )t ]
Интенсивность флуоресценции (люминесценции) убывает экспоненциально,
причём время, за которое она уменьшается в e раз, равно   f /( f  g )
4 Модель Вольтера «хищник-жертва»
Физико-математическое моделирование биологических процессов началось с
модели автокаталитической химической реакции, предложенной Лотка(1930 г).
В некотором замкнутом районе живут хищники и их жёртвы, скажем, рыси и
зайцы. Рыси питаются только зайцами, зайцы –растительной пищей, запас которой
избыточен. Число зайцев – X, число рысей-Y. Поведение популяций во времени
описывается уравнениями
X t  k1 X  kXY,
Yt  k XY  k 2Y .
Константа k1 характеризует размножение жертв, k – их убыль в результате встреч с
хищниками, k  - размножение хищников, для которых необходимо питание
хищников, т. е. встречи с жертвами, k 2 -вымирание хищников. Получена
нелинейная система уравнений. Заметим, однако, что трудно ожидать больших
одновременных отклонений X и Y от равновесных значений X 0 и Y0 . Поэтому
удобно искать решения в виде
X (t )  X 0  xet
.
Где X  X 0 , Y  Y0
Y (t )  Y0  ye t
,
Подставив эти выражения для X и Y в исходную систему, получим
X  xe   k X  xe   k X  xe Y  ye 
Y  ye   k X  xe Y  ye   k Y  ye ;
t
t
0
1
t
0
t
t
0
t
o
0
0
t
0
e
2
0
k1 X 0  kX 0Y0  k X 0Y0  k2Yo  0 X  X 0 , Y  Y0 
kk
x  1 y  0
k

k k 2
x  y  0
k
Условие совместимости этих двух уравнений есть характеристическое уравнение
2  k1k 2  0 , и   iw -мнимая величина, таким образом,
X  X 0  Aconstwt, Y  Y0  B coswt   0 
Частота колебаний w  k1k 2  2 и не зависит от k , k  , Амплитуда колебаний, как
1
следует из (б) и характеристического уравнения, относятся как
k
k 2 / k1
A/B= k 
Таким образом, популяции X и Y испытывают периодические колебания
одинаковой частоты, смещённые по фазе. Отражает ли такая модель
действительные свойства изучаемой системы? Приведём рисунок, на котором
представлена динамика популяций зайцев и рысей в Канаде за 1845-1935 г г.
Видим, что основные особенности отражены вполне чётко, и простая модель дала
вполне приемлемые результаты, что и требовалось.
тыс
шт
заяц
рысь
120
80
40
1850
1870
1890
1910
1930
Как видно из приведённых примеров, при составление дифференциальных
уравнений, описывающих систему, необходимо выделить основные
закономерности её развития, пренебрегая менее важными, иногда в процессе
решения отбрасывают лишнюю информацию, введённую в модуль ( как в
последнем примере). Метод матесатического моделирования позволяет получить
хорошие результаты без уточнения механизма происходящего явления, более того,
Позволяет путём анализа результатов сделать определённые выводы, касающиеся
природы изучаемого явления или наметить пути его дальнейшего изучения,
выявить раннее незамеченные закономерности, оценить относительную значимость
составляющих картину и т. д.