ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ
реклама

ÂÛÑØÅÅ ÏÐÎÔÅÑÑÈÎÍÀËÜÍÎÅ ÎÁÐÀÇÎÂÀÍÈÅ
А. К. НАРЫШКИН
ЦИФРОВЫЕ УСТРОЙСТВА
И МИКРОПРОЦЕССОРЫ
Рекомендовано
Учебным управлением Московского энергетического института
(Технического университета) в качестве учебного пособия
для студентов высших учебных заведений
радиотехнических специальностей
Ìîñêâà
2006
1
ÓÄÊ 621.377.6 (075.8)
ÁÁÊ 32.84ÿ73
Í308
Ð å ö å í ç å í ò û:
çàì. äèðåêòîðà ÔÃÓÏ ÍÈÊÔÈ, çàâ. ëàáîðàòîðèåé ýëåêòðîàêóñòèêè ÍÈÊÔÈ,
êàíä. òåõí. íàóê Ê. Â. Íåâåðîâñêèé;
çàâ. ëàáîðàòîðèåé öèôðîâûõ ìåòîäîâ îáðàáîòêè ñèãíàëîâ
ÍÈÊÔÈ Þ. Í. Áàðûøíåíêîâ;
äîöåíò êàôåäðû êîíñòðóèðîâàíèÿ è ïðîèçâîäñòâà
ÐÝÑ ÌÃÈÐÝÀ, êàíä. òåõí. íàóê À. Í. Áîãà÷åíêîâ
Í308
Íàðûøêèí À.Ê.
Öèôðîâûå óñòðîéñòâà è ìèêðîïðîöåññîðû: Ó÷åá. ïîñîáèå
äëÿ ñòóä. âûñø. ó÷åá. çàâåäåíèé / Àëåêñàíäð Êèðèëëîâè÷ Íàðûøêèí. Ì.: Èçäàòåëüñêèé öåíòð «Àêàäåìèÿ», 2006. 320 ñ.
ISBN 5-7695-1618-6
Ðàññìàòðèâàþòñÿ îñíîâû àëãåáðû ëîãèêè, òåîðèè ïåðåêëþ÷àòåëüíûõ
ôóíêöèé, òåîðèè àñèíõðîííûõ ïîòåíöèàëüíûõ è ñèíõðîííûõ àâòîìàòîâ,
ñèíòåç öèôðîâûõ óçëîâ (òðèããåðîâ, ñ÷åò÷èêîâ, ñäâèãàþùèõ ðåãèñòðîâ,
ìóëüòèïëåêñîðîâ, äåìóëüòèïëåêñîðîâ, ñóììàòîðîâ), ïðèìåíåíèå èíòåãðàëüíûõ ñõåì äëÿ ïðîåêòèðîâàíèÿ öèôðîâûõ óñòðîéñòâ, à òàêæå àðõèòåêòóðà, ñèñòåìà êîìàíä, øèííûå ïðèåìîïåðåäàò÷èêè, ïðîåêòèðîâàíèå
ìèêðîêîíòðîëëåðîâ íà ìèêðîïðîöåññîðàõ, ðàçðàáîòêà ïðîãðàììíîãî îáåñïå÷åíèÿ. Íàðÿäó ñ èçâåñòíûìè ïðèâîäÿòñÿ ðàçðàáîòàííûå àâòîðîì â ïîñëåäíèå ãîäû íîâûå ìåòîäèêè àíàëèçà è ñèíòåçà öèôðîâûõ óñòðîéñòâ.
Äëÿ ñòóäåíòîâ âóçîâ ðàäèîòåõíè÷åñêèõ ñïåöèàëüíîñòåé. Ìîæåò áûòü ïîëåçíî ñòóäåíòàì òåõíèêóìîâ ðàäèîòåõíè÷åñêîãî ïðîôèëÿ.
ÓÄÊ 621.377.6(075.8)
ÁÁÊ 32.84ÿ73
Îðèãèíàë-ìàêåò äàííîãî èçäàíèÿ ÿâëÿåòñÿ ñîáñòâåííîñòüþ
Èçäàòåëüñêîãî öåíòðà «Àêàäåìèÿ», è åãî âîñïðîèçâåäåíèå ëþáûì ñïîñîáîì
áåç ñîãëàñèÿ ïðàâîîáëàäàòåëÿ çàïðåùàåòñÿ
ISBN 5-7695-1618-6
2
© Íàðûøêèí À. Ê., 2006
© Èçäàòåëüñêèé öåíòð «Àêàäåìèÿ», 2006
ÎÃËÀÂËÅÍÈÅ
Ñïèñîê ñîêðàùåíèé ..................................................................................... 3
Ñïèñîê óñëîâíûõ îáîçíà÷åíèé ................................................................... 5
Ïðåäèñëîâèå ................................................................................................. 8
Ââåäåíèå ...................................................................................................... 10
ÐÀÇÄÅË I
ÎÑÍÎÂÛ ÀËÃÅÁÐÛ ËÎÃÈÊÈ
à ë à â à 1. Îñíîâíûå îáîçíà÷åíèÿ è ïîñòóëàòû .......................................... 17
1.1. Îñíîâíûå âûñêàçûâàíèÿ è ïåðåìåííûå ........................................ 17
1.2. Îñíîâíûå ëîãè÷åñêèå îïåðàöèè ..................................................... 18
1.3. Îñíîâíûå ïîñòóëàòû àëãåáðû ëîãèêè ............................................ 20
1.4. Îáðàòíûå ëîãè÷åñêèå îïåðàöèè ..................................................... 21
à ë à â à 2. Àíàëèòè÷åñêèå ôîðìû ïðåäñòàâëåíèÿ ëîãè÷åñêèõ ôóíêöèé ....... 23
2.1. Ñîâåðøåííàÿ äèçúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà ........................ 23
2.2. Ñîêðàùåííûå, òóïèêîâûå è ìèíèìàëüíûå äèçúþíêòèâíûå
íîðìàëüíûå ôîðìû ïðåäñòàâëåíèÿ ôóíêöèé ............................... 28
2.3. Ñîâåðøåííàÿ êîíúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà ....................... 31
2.4. Ïðåäñòàâëåíèå ôóíêöèé ñ íå ïîëíîñòüþ çàäàííûìè
àðãóìåíòàìè â äèçúþíêòèâíîé íîðìàëüíîé ôîðìå ..................... 34
à ë à â à 3. Ìèíèìèçàöèÿ ëîãè÷åñêèõ ôóíêöèîíàëîâ ñ ïîìîùüþ ÝÂÌ ..... 37
3.1. Ñòðóêòóðà ïðîãðàììû ìèíèìèçàöèè ëîãè÷åñêîãî
ôóíêöèîíàëà .................................................................................... 37
3.2. Ââîä èñõîäíîãî ëîãè÷åñêîãî ôóíêöèîíàëà â ÝÂÌ ....................... 38
3.3. Îïðåäåëåíèå ôîðìû ïðåäñòàâëåíèÿ ìèíèìèçèðóåìîé
ôóíêöèè ........................................................................................... 39
3.4. Ñêëåèâàíèå ñîïðÿæåííûõ ìèíòåðìîâ è èìïëèêàíò .................... 40
3.5. Èñêëþ÷åíèå èçáûòî÷íûõ èìïëèêàíò ............................................. 43
à ë à â à 4. Ïðåäñòàâëåíèå è ìèíèìèçàöèÿ ëîãè÷åñêèõ ôóíêöèé
ñ ïîìîùüþ äèàãðàìì ................................................................... 46
4.1. Äèàãðàììû Âåé÷à è êàðòû Êàðíî .................................................. 46
4.2. Àëãåáðàè÷åñêèå äèàãðàììû ............................................................ 49
4.3. Âûïîëíåíèå îïåðàöèé íàä ëîãè÷åñêèìè ôóíêöèÿìè
ñ ïîìîùüþ äèàãðàìì Âåé÷à .......................................................... 51
à ë à â à 5. Ëîãè÷åñêèå ôóíêöèè äâóõ ïåðåìåííûõ ....................................... 52
5.1. Òàáëèöû èñòèííîñòè, íàçâàíèÿ, àíàëèòè÷åñêèå âûðàæåíèÿ è
ñâîéñòâà ôóíêöèé äâóõ ïåðåìåííûõ .............................................. 52
315
5.2. Ïðèíöèï äâîéñòâåííîñòè ............................................................... 54
5.3. Îáðàòíûå ëîãè÷åñêèå ôóíêöèè äâóõ ïåðåìåííûõ ........................ 56
5.4. Ôóíêöèîíàëüíàÿ ïîëíîòà ëîãè÷åñêèõ ôóíêöèé ........................... 57
5.5. Ïðåäñòàâëåíèå ëîãè÷åñêèõ ôóíêöèé â ñèñòåìå Word ................... 58
Ð À Ç Ä Å Ë II
ÊÎÌÁÈÍÀÖÈÎÍÍÛÅ ÖÈÔÐÎÂÛÅ ÓÑÒÐÎÉÑÒÂÀ
à ë à â à 6. Îñíîâíûå ëîãè÷åñêèå ýëåìåíòû ................................................. 61
6.1. Áàçîâûå ëîãè÷åñêèå ýëåìåíòû, ðåàëèçóþùèå ôóíêöèè
äâóõ àðãóìåíòîâ ............................................................................... 61
6.2. Âçàèìîçàìåíÿåìîñòü ëîãè÷åñêèõ ýëåìåíòîâ .................................. 65
6.3. Ëîãè÷åñêèå ýëåìåíòû È ÈËÈ è È ÈËÈ ÍÅ ....................... 72
à ë à â à 7. Ìåòîäèêà àíàëèçà è ñèíòåçà êîìáèíàöèîííûõ öèôðîâûõ
óñòðîéñòâ ..................................................................................... 76
7.1. Ïðåîáðàçîâàòåëü êîäà Ãðåÿ â íàòóðàëüíûé äâîè÷íûé êîä ........... 76
7.2. Ìåòîäèêà ñèíòåçà êîìáèíàöèîííûõ öèôðîâûõ óñòðîéñòâ .......... 80
7.3. Ñèíòåç øèôðàòîðà è äåøèôðàòîðà êîäà,
ïîçâîëÿþùåãî îáíàðóæèâàòü îäèíî÷íûå îøèáêè ........................ 81
7.4. Øèôðàòîð è äåøèôðàòîð êîäà Õýììèíãà,
èñïðàâëÿþùåãî îäèíî÷íóþ îøèáêó .............................................. 84
à ë à â à 8. Øèôðàòîðû è äåøèôðàòîðû ...................................................... 89
8.1. Øèôðàòîðû ...................................................................................... 89
8.2. Ïðèîðèòåòíûå øèôðàòîðû ............................................................. 92
8.3. Äåøèôðàòîðû ................................................................................... 96
à ë à â à 9. Ìóëüòèïëåêñîðû è äåìóëüòèïëåêñîðû ..................................... 100
9.1. Ìóëüòèïëåêñîðû ............................................................................ 100
9.2. Äåìóëüòèïëåêñîðû ......................................................................... 107
à ë à â à 10. Ñóììàòîðû ............................................................................... 108
10.1. Îäíîðàçðÿäíûå ñóììàòîðû ......................................................... 108
10.2. Ìíîãîðàçðÿäíûå àðèôìåòè÷åñêèå ñóììàòîðû .......................... 111
10.3. Îäíî- è ìíîãîðàçðÿäíûå àëãåáðàè÷åñêèå ñóììàòîðû .............. 116
10.4. Ñóììàòîðû ÷èñåë, ïðåäñòàâëåííûõ â ôîðìàòå
ñ ïëàâàþùåé çàïÿòîé ................................................................. 120
10.5. Àðèôìåòè÷åñêèå óìíîæèòåëè ..................................................... 123
à ë à â à 11. Öèôðîâûå êîìïàðàòîðû ......................................................... 125
11.1. Îäíîðàçðÿäíûå êîìïàðàòîðû ..................................................... 125
11.2. Ìíîãîðàçðÿäíûå êîìïàðàòîðû ................................................... 126
à ë à â à 12. Êîìáèíàöèîííûå öèôðîâûå óñòðîéñòâà íà îñíîâå
ïðîãðàììèðóåìûõ èíòåãðàëüíûõ ñõåì .................................... 131
12.1. Êëàññèôèêàöèÿ ïðîãðàììèðóåìûõ èíòåãðàëüíûõ ñõåì ............ 131
12.2. Ïðîãðàììèðóåìûå ïîñòîÿííûå çàïîìèíàþùèå óñòðîéñòâà .... 134
12.3. Ïðîãðàììèðóåìûå ëîãè÷åñêèå ìàòðèöû .................................... 136
12.4. Ïðîãðàììèðóåìûå ëîãè÷åñêèå èíòåãðàëüíûå ñõåìû ................ 138
316
Ð À Ç Ä Å Ë III
ÏÎÑËÅÄÎÂÀÒÅËÜÍÎÑÒÍÛÅ ÖÈÔÐÎÂÛÅ ÓÑÒÐÎÉÑÒÂÀ
à ë à â à 13. Îáùèå ñâåäåíèÿ î ïîñëåäîâàòåëüíîñòíûõ öèôðîâûõ
óñòðîéñòâàõ .............................................................................. 146
13.1. Îïðåäåëåíèå ïîíÿòèÿ .................................................................. 146
13.2. Êëàññèôèêàöèÿ ............................................................................ 147
13.3. Ìåòîäèêà ñèíòåçà ........................................................................ 148
à ë à â à 14. Òðèããåðû .................................................................................. 150
14.1. RS-òðèããåðû .................................................................................. 150
14.2. Ñèíõðîííûå D-òðèããåðû ............................................................. 158
14.3. T-òðèããåðû .................................................................................... 163
14.4. JK-òðèããåðû .................................................................................. 168
14.5. Âçàèìîçàìåíÿåìîñòü òðèããåðîâ ................................................... 173
à ë à â à 15. Ñ÷åò÷èêè .................................................................................. 179
15.1. Êëàññèôèêàöèÿ è îñíîâíûå ïàðàìåòðû .................................... 179
15.2. Ñèíõðîííûå äâîè÷íûå ñ÷åò÷èêè ................................................ 180
15.3. Àñèíõðîííûå äâîè÷íûå ñ÷åò÷èêè .............................................. 194
15.4. Àñèíõðîííûå íåäâîè÷íûå ñ÷åò÷èêè .......................................... 198
à ë à â à 16. Ðåãèñòðû .................................................................................. 206
16.1. Îáùèå ñâåäåíèÿ ........................................................................... 206
16.2. Ðåãèñòðû ïàìÿòè .......................................................................... 207
16.3. Ðåãèñòðû ñäâèãà ........................................................................... 217
16.4. Êîìáèíèðîâàííûå ðåãèñòðû ....................................................... 227
16.5. Ðåãèñòðû ïîñëåäîâàòåëüíûõ ïðèáëèæåíèé ................................ 230
Ð À Ç Ä Å Ë IV
ÌÈÊÐÎÏÐÎÖÅÑÑÎÐÛ
à ë à â à 17. Àðõèòåêòóðà ............................................................................. 239
17.1. Ñòðóêòóðà è ïðèíöèï ôóíêöèîíèðîâàíèÿ ÝÂÌ ...................... 239
17.2. Êëàññèôèêàöèÿ ìèêðîïðîöåññîðíûõ êîìïëåêòîâ
èíòåãðàëüíûõ ñõåì ...................................................................... 240
17.3. Îäíîêðèñòàëüíûå ìèêðîïðîöåññîðû ......................................... 242
17.4. Ïðèíöèïû ïîñòðîåíèÿ ìîäóëüíûõ ìèêðîïðîöåññîðîâ ............ 247
à ë à â à 18. Ñèñòåìû êîìàíä ...................................................................... 252
18.1. Îáùèå ñâåäåíèÿ ........................................................................... 252
18.2. Êîìàíäû îäíîêðèñòàëüíûõ ìèêðîïðîöåññîðîâ ........................ 254
18.3. Ðàñøèðåííûå íàáîðû êîìàíä ìèêðîïðîöåññîðîâ .................... 259
à ë à â à 19. Øèííûå ïðèåìîïåðåäàò÷èêè .................................................. 264
19.1. Ìíîãîðåæèìíûå áóôåðíûå ðåãèñòðû ........................................ 264
19.2. Äðàéâåðû äâóíàïðàâëåííîé ìàãèñòðàëè .................................... 266
à ë à â à 20. Àðèôìåòèêî-ëîãè÷åñêîå óñòðîéñòâî ....................................... 267
20.1. Ñòðóêòóðà àðèôìåòèêî-ëîãè÷åñêîãî óñòðîéñòâà ....................... 267
20.2. Ôîðìèðîâàíèå îïåðàíäîâ X è Y ñóììàòîðà .............................. 267
317
20.3. Ñóììàòîð ÀËÓ .............................................................................. 273
20.4. Ñäâèãàòåëü ÀËÓ ............................................................................ 277
20.5. Ìóëüòèïëåêñîð I è ìóëüòèïëåêñîð àêêóìóëÿòîðà ..................... 278
20.6. Îïåðàöèè ïåðåñûëêè èíôîðìàöèè â ÀËÓ ................................ 279
20.7. Áûñòðîäåéñòâèå ÀËÓ ................................................................... 281
à ë à â à 21. Ðàçðàáîòêà ïðîãðàììíîãî îáåñïå÷åíèÿ .................................. 283
21.1. Îáùèå ñâåäåíèÿ ........................................................................... 283
21.2. ßçûêè ïðîãðàììèðîâàíèÿ ........................................................... 284
21.3. Ñïîñîáû àäðåñàöèè ...................................................................... 287
21.4. Ñòàíäàðòíàÿ ôîðìà ïðåäñòàâëåíèÿ ïðîãðàììû
íà ÿçûêå àññåìáëåðà ................................................................... 292
à ë à â à 22. Ìèêðîêîíòðîëëåðû ................................................................. 296
22.1. Êëàññèôèêàöèÿ ............................................................................ 296
22.2. Ïðîãðàììíîå îáåñïå÷åíèå ìèêðîêîíòðîëëåðîâ ....................... 297
22.3. Ñòðóêòóðà ìèêðîêîíòðîëëåðîâ ñåìåéñòâà AT89C ..................... 301
à ë à â à 23. Ôóíêöèîíàëüíûå óçëû ìèêðîïðîöåññîðíîé ñèñòåìû ............ 303
23.1. Óñòðîéñòâà êîäèðîâàíèÿ ñèãíàëîâ êëàâèàòóðû
ïóëüòà îïåðàòîðà ......................................................................... 303
23.2. Óñòðîéñòâà è àëãîðèòìû óñòðàíåíèÿ äðåáåçãà
êëàâèøíûõ êîíòàêòîâ ................................................................. 305
23.3. Ñâåòîâûå èíäèêàòîðíûå óñòðîéñòâà .......................................... 308
Ñïèñîê ëèòåðàòóðû ................................................................................... 312
318
ÑÏÈÑÎÊ ÑÎÊÐÀÙÅÍÈÉ
À
ÀËÓ
ÀÖÏ
ÁÈÑ
ÁÌÊ
ÁÐ
ÁÐÀ
ÁÐÄ
ÃÏÌÑ
ÃÒÈ
ÄÁß
ÄÍÔ
ÄØÊ
ÇÓ
ÇÝ
ÈÌÑ
ÈÑ
ÊÁß
ÊÌÎÏ
ÊÎÈ
ÊÖÓ
ËÁ
ËÈÏÇ
ËÝ
ÌÀ
ÌÁÀ
ÌÁÐ
ÌÄ
ÌÊ
ÌËÁ
ÌÍÎÏ
ÌÎÏ
ÌÏ
ÌÏÊ
ÌÓ
ÍÄÊ
ÍÌÄ
ÎÇÓ
àêêóìóëÿòîð
àðèôìåòèêî-ëîãè÷åñêîå óñòðîéñòâî
àíàëîãî-öèôðîâîé ïðåîáðàçîâàòåëü
áîëüøàÿ èíòåãðàëüíàÿ ñõåìà
áàçîâûé ìàòðè÷íûé êðèñòàëë
áóôåðíûé ðåãèñòð
áóôåðíûé ðåãèñòð àäðåñà
áóôåðíûé ðåãèñòð äàííûõ
ãëîáàëüíàÿ ïðîãðàììèðóåìàÿ ìàòðèöà ñîåäèíåíèé
ãåíåðàòîð òàêòîâûõ èìïóëüñîâ
äèçúþíêòèâíàÿ áèñòàáèëüíàÿ ÿ÷åéêà
äèçúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà
äåøèôðàòîð êîìàíä
çàïîìèíàþùåå óñòðîéñòâî
çàïîìèíàþùèé ýëåìåíò
èíòåãðàëüíàÿ ìèêðîñõåìà
èíòåãðàëüíàÿ ñõåìà
êîíúþíêòèâíàÿ áèñòàáèëüíàÿ ÿ÷åéêà
êîìïëåìåíòàðíûé ÌÎÏ-ýëåìåíò
êîä îïåðàöèè èíäèêàòîðà
êîìáèíàöèîííîå öèôðîâîå óñòðîéñòâî
ëîãè÷åñêèé áëîê
ëàâèííî-èíæåêöèîííûé ñ ïëàâàþùèì çàòâîðîì
ëîãè÷åñêèé ýëåìåíò
ìàãèñòðàëü àäðåñà
ìëàäøèé áàéò àäðåñà
ìíîãîðåæèìíûé áóôåðíûé ðåãèñòð
ìàãèñòðàëü äàííûõ
ìèêðîêîíòðîëëåð
ìàòðè÷íûé ëîãè÷åñêèé áëîê
ìåòàëë íèòðèä êðåìíèÿ îêñèä êðåìíèÿ ïîëóïðîâîäíèê
ìåòàëë îêñèä ïîëóïðîâîäíèê
ìèêðîïðîöåññîð
ìèêðîïðîöåññîðíûé êîìïëåêò
ìàãèñòðàëü óïðàâëåíèÿ
íàòóðàëüíûé äâîè÷íûé êîä
êîíòðîëëåð íà æåñòêîì ìàãíèòíîì äèñêå
îïåðàòèâíîå çàïîìèíàþùåå óñòðîéñòâî
3
ÎÓ
ÏÂÌ
ÏÇÓ
ÏÊÌÁ
ÏËÈÑ
ÏËÌ
ÏÌË
ÏÏÇÓ
ÏÖÓ
ÐÀ
ÐÊ
ÐÌÏ
ÐÎÍ
ÐÏ
ÐÏÇÓ
ÑÀÏÐ
ÑÁÀ
ÑÄÍÔ
ÑÈÑ
ÑÊÍÔ
ÑÓÏ
ÒÏ
ÒÒË
ÒÒËØ
ÓÂÂ
ÓÂÕ
ÓÃÎ
ÓÓ
ÔÑÓ
ÖÀÏ
ÖÂÌ
ÖÎÑ
ÖÏÝ
ÖÓ
ØÄ
ØÔ
ÝÏË
ÝÏÏÇÓ
ÝÑË
ÝÔË
4
îïåðàöèîííûé óñèëèòåëü
ïðîãðàììèðóåìàÿ âåíòèëüíàÿ ìàòðèöà
ïîñòîÿííîå çàïîìèíàþùåå óñòðîéñòâî
ïðîãðàììèðóåìûé êîììóòèðóåìûé ìàòðè÷íûé áëîê
ïðîãðàììèðóåìàÿ ëîãè÷åñêàÿ èíòåãðàëüíàÿ ñõåìà
ïðîãðàììèðóåìàÿ ëîãè÷åñêàÿ ìàòðèöà
ïðîãðàììèðóåìàÿ ìàòðè÷íàÿ ëîãèêà, ïðîãðàììèðóåìàÿ ìàêðîëîãèêà
ïðîãðàììèðóåìîå ïîñòîÿííîå çàïîìèíàþùåå óñòðîéñòâî
ïîñëåäîâàòåëüíîñòíîå öèôðîâîå óñòðîéñòâî
ðåãèñòð àäðåñà
ðåãèñòð êîìàíä
ðåêîíôèãóðèðóåìûé ìîäóëü ïàìÿòè
ðåãèñòð îáùåãî íàçíà÷åíèÿ
ðåãèñòð ïðèçíàêîâ
ðåïðîãðàììèðóåìîå ïîñòîÿííîå çàïîìèíàþùåå óñòðîéñòâî
ñèñòåìà àâòîìàòèçèðîâàííîãî ïðîåêòèðîâàíèÿ
ñòàðøèé áàéò àäðåñà
ñîâåðøåííàÿ äèçúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà
ñðåäíÿÿ èíòåãðàëüíàÿ ñõåìà
ñîâåðøåííàÿ êîíúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà
ñåêöèÿ óñêîðåííîãî ïåðåíîñà
òàáëèöà ïåðåêîäèðîâêè
òðàíçèñòîðíî-òðàíçèñòîðíàÿ ëîãèêà
ÒÒË ñ äèîäàìè Øîòòêè
óñòðîéñòâî ââîäà-âûâîäà
óñòðîéñòâî âûáîðêè è õðàíåíèÿ
óñëîâíîå ãðàôè÷åñêîå îáîçíà÷åíèå
óñòðîéñòâî óïðàâëåíèÿ
ôîðìèðîâàòåëü ñèãíàëîâ óïðàâëåíèÿ
öèôðîàíàëîãîâûé ïðåîáðàçîâàòåëü
öèôðîâàÿ âû÷èñëèòåëüíàÿ ìàøèíà
öèôðîâàÿ îáðàáîòêà ñèãíàëà
öåíòðàëüíûé ïðîöåññîðíûé ýëåìåíò
öèôðîâîå óñòðîéñòâî
øèííûé äðàéâåð
øèííûé ôîðìèðîâàòåëü
ëîãèêà íà ýìèòòåðíûõ ïîâòîðèòåëÿõ
ýëåêòðè÷åñêè ïðîãðàììèðóåìîå ïîñòîÿííîå çàïîìèíàþùåå
óñòðîéñòâî
ýìèòòåðíî-ñâÿçàííàÿ ëîãèêà
ýìèòòåðíî-ôóíêöèîíàëüíàÿ ëîãèêà
ÑÏÈÑÎÊ ÓÑËÎÂÍÛÕ ÎÁÎÇÍÀ×ÅÍÈÉ
&, ·, ∧
⊕
∼
∆
↓
⊃
∗, ½
/
\
==
=1
1, ∨
A
ÀÂ
AC
A/D
ALU
B
BUBR
C, CLK
CARG
c.d.
c.u.
CD
CLR
CRG
CRI
CRO
CRP
CS
CT
CY
D
NOT, ÍÅ îïåðàöèÿ ëîãè÷åñêîãî îòðèöàíèÿ (èíâåðñèÿ)
AND, È îïåðàöèÿ ëîãè÷åñêîãî óìíîæåíèÿ (êîíúþíêöèÿ)
îïåðàöèÿ ñóììèðîâàíèÿ ïî ìîäóëþ 2, íåðàâíîçíà÷íîñòü
ðàâíîçíà÷íîñòü
îïåðàöèÿ çàïðåòà
ñòðåëêà Ïèðñà
èìïëèêàöèÿ
øòðèõ Øåôôåðà
íåîïðåäåëåííîñòü, ôàêóëüòàòèâ, çàïðåùåííîå ñîñòîÿíèå
ëîãè÷åñêîå äåëåíèå
ëîãè÷åñêîå âû÷èòàíèå
êîìïàðàòîð
ýëåìåíò íåðàâíîçíà÷íîñòè, ñóììàòîð ïî ìîäóëþ 2
OR, ÈËÈ îïåðàöèÿ ëîãè÷åñêîãî ñëîæåíèÿ (äèçúþíêöèÿ)
address àäðåñ; accumulator àêêóìóëÿòîð
address bus àäðåñíàÿ øèíà
analog comparator àíàëîãîâûé êîìïàðàòîð
analog-digital àíàëîãî-öèôðîâîé
arithmetic and logic unit àðèôìåòèêî-ëîãè÷åñêîå óñòðîéñòâî
binary áèíàðíûé; äâîè÷íûé; bit áèò, äâîè÷íûé ðàçðÿä
bidirectional unibus buffer register äâóíàïðàâëåííûé áóôåðíûé ðåãèñòð îáùåé øèíû
clock ñèãíàë ñèíõðîíèçàöèè
consecutive approximation register ðåãèñòð ïîñëåäîâàòåëüíûõ
ïðèáëèæåíèé
count down ñ÷èòàòü â îáðàòíîì íàïðàâëåíèè
count up ñ÷èòàòü â ïðÿìîì íàïðàâëåíèè
coder øèôðàòîð
clear î÷èùàòü
carry of group ñèãíàë ãðóïïîâîãî ïåðåíîñà
carry input âõîäíîé ñèãíàë ïåðåíîñà
carry out put âûõîäíîé ñèãíàë ïåðåíîñà
carry prompting ðàçðåøåíèå ãðóïïîâîãî ïåðåíîñà
chi p select âûáîð ìèêðîñõåìû
counter ñ÷åò÷èê
carry ïåðåíîñ; ñèãíàë ïåðåíîñà
datà èíôîðìàöèîííûå äàííûå; delay çàäåðæêà, çàïàçäûâàíèå; decimal äåñÿòè÷íûé
5
DA
D/A
DB
DC
DD
DM
DVD
DVS
E, EN
F
FR
G
GRD
GS
H
HA
HS
I
IB
INT
I/OR
I/OW
L
l
MBR
MD
MEMR
MEMW
MPL
MX
O
OB
OF
P
PAL
PC
PCD
PLA
PLD
PR
PROM
Q
6
differential amplifier äèôôåðåíöèàëüíûé óñèëèòåëü
digital-analog öèôðîàíàëîãîâûé
data bus øèíà äàííûõ, èíôîðìàöèîííàÿ øèíà
decoder äåøèôðàòîð
digital device öèôðîâîé ýëåìåíò
demulti plexer äåìóëüòèïëåêñîð
dividend äåëèìîå
divisor äåëèòåëü
enable ðàçðåøàþùèé ñèãíàë, ðàçðåøåíèå; ðàçðåøàþùèé
âõîä
function ôóíêöèÿ
flag register ôëàãîâûé ðåãèñòð; ðåãèñòð ïðèçíàêà
carry generator ãåíåðàòîð ñèãíàëà ïåðåíîñà; generator ãåíåðàòîð
ground îáùàÿ øèíà, çåìëÿ
gate signal ñòðîá-ñèãíàë ñòðîáèðóþùèé ñèãíàë
high âûñîêèé; hexadecimal øåñòíàäöàòåðè÷íûé
half-adder ïîëóñóììàòîð
half-summator ïîëóñóììàòîð
input âõîä
input bus âõîäíàÿ øèíà
interrupt ïðåðûâàíèå
input/output read ñ÷èòûâàíèå èç óñòðîéñòâà ââîäà/âûâîäà
input/output write çàïèñü â óñòðîéñòâî ââîäà/âûâîäà
low íèçêèé
line ñòðîêà
multiregime buffer register ìíîãîðåæèìíûé áóôåðíûé ðåãèñòð
mode ðåæèì ðàáîòû
memory read ñ÷èòûâàíèå èç ïàìÿòè
memory write çàïèñü â ïàìÿòü
multi plier ìíîæèòåëü; ñîìíîæèòåëü; óìíîæèòåëü
multi plexer ìóëüòèïëåêñîð; êîììóòàòîð
output âûõîä; âûâîä; âûõîäíîå óñòðîéñòâî; óñòðîéñòâî âûâîäà
output bus âûõîäíàÿ øèíà
overflow ïåðåïîëíåíèå; ïðèçíàê ïåðåïîëíåíèÿ
propagation ðàñïðîñòðàíåíèå; product ïðîèçâåäåíèå äâóõ ÷èñåë
programmable array logic ïðîãðàììèðóåìàÿ ìàòðè÷íàÿ ëîãèêà
program counter ïðîãðàììíûé ñ÷åò÷èê, ñ÷åò÷èê êëìàíä; parity
of carry êîíòðîëü ÷åòíîñòè ïåðåíîñà
priority-oriented coder ïðèîðèòåòíûé øèôðàòîð
programmable logic array ïðîãðàììèðóåìàÿ ëîãè÷åñêàÿ ìàòðèöà
programmable logic device ïðîãðàììèðóåìîå ëîãè÷åñêîå óñòðîéñòâî
parity of result êîíòðîëü ÷åòíîñòè ïåðåíîñà
programmable read-only memory ïðîãðàììèðóåìàÿ ïîñòîÿííàÿ ïàìÿòü, ïðîãðàììèðóåìîå ïîñòîÿííîå ÇÓ
quotien ÷àñòíîå; îòíîøåíèå
R reset âîññòàíàâëåíèå, âîçâðàò â èñõîäíîå ïîëîæåíèå; óñòàíîâêà â «0»; reverse ðåâåðñ, îáðàòíûé õîä; receiver ïðèåìíèê
RG register ðåãèñòð
S set óñòàíàâëèâàòü; sign çíàê; sum ñóììà; switch ïåðåêëþ÷àòåëü
SIB scale index byte áàéò ìàñøòàáèðóåìîãî èíäåêñà
SM summator ñóììàòîð, ñóììèðóþùåå óñòðîéñòâî
SP stack pointer óêàçàòåëü ñòåêà
STB strobe ñòðîá-èìïóëüñ, ñòðîáèðóþùèé èìïóëüñ
T trigger òðèããåð; ïóñêîâàÿ ñõåìà; transmitter ïåðåäàò÷èê;
topple îïðîêèäûâàòüñÿ; time âðåìÿ
V veto çàïðåò
W write çàïèñü
Z zero íóëü
ZD zero definition çàäàíèå íóëÿ; zero drift øóìîïîäàâèòåëü
7
ÏÐÅÄÈÑËÎÂÈÅ
Ó÷åáíîå ïîñîáèå ÿâëÿåòñÿ îáîáùåíèåì ìíîãîëåòíåãî íàó÷íîìåòîäè÷åñêîãî è ïðàêòè÷åñêîãî îïûòà àâòîðà.
Ïîìèìî èçâåñòíûõ ìåòîäèê àâòîð èñïîëüçóåò ðàçðàáîòàííûå
èì íîâûå ìåòîäèêè àíàëèçà è ñèíòåçà öèôðîâûõ óñòðîéñòâ.  êà÷åñòâå ïðèìåðîâ ïðèâîäÿòñÿ ôóíêöèè, èìåþùèå ïðàêòè÷åñêîå çíà÷åíèå.
 ïåðâîì ðàçäåëå ïðåäëàãàåìîãî ó÷åáíîãî ïîñîáèÿ ïðèâåäåíû
âñå îñíîâíûå ïîëîæåíèÿ ñîâðåìåííîé àëãåáðû ëîãèêè.
 ïåðâîé ãëàâå ïðèâåäåíû îñíîâíûå îáîçíà÷åíèÿ è ïîñòóëàòû
áèíàðíîé (àðèñòîòåëåâîé) àëãåáðû ëîãèêè.
Âî âòîðîé ãëàâå ðàññìîòðåíû îñíîâíûå ëîãè÷åñêèå ôóíêöèè è
èõ ñâîéñòâà.
 òðåòüåé ãëàâå îáñóæäàþòñÿ àëãîðèòìû ïðîãðàìì, ïîçâîëÿþùèõ ìèíèìèçèðîâàòü ëîãè÷åñêèå ôóíêöèè ñ ïîìîùüþ êîìïüþòåðíîé òåõíèêè.
 ÷åòâåðòîé ãëàâå ïðåäñòàâëåíî ïðèìåíåíèå àðèôìåòè÷åñêèõ è
àëãåáðàè÷åñêèõ äèàãðàìì.
 ïÿòîé ãëàâå èññëåäîâàíû âñå ôóíêöèè äâóõ ïåðåìåííûõ, èõ
ñâîéñòâà è âçàèìîñâÿçü.
Âòîðîé ðàçäåë ïîñâÿùåí êîìáèíàöèîííûì öèôðîâûì óñòðîéñòâàì, êîòîðûå îòëè÷àþòñÿ îò ïîñëåäîâàòåëüíîñòíûõ òåì, ÷òî ó
íèõ íåò ïàìÿòè ïî ïðåäûäóùåìó ñîñòîÿíèþ. Êîìáèíàöèîííûå öèôðîâûå óñòðîéñòâà (ÊÖÓ) ðåàëèçóþò çàäàííûå ìàòåìàòè÷åñêèå è
ëîãè÷åñêèå îïåðàöèè íàä äåéñòâóþùèìè â äàííûé ìîìåíò âðåìåíè êîìáèíàöèÿìè âõîäíûõ èíôîðìàöèîííûõ ñèãíàëîâ â ñîîòâåòñòâèè ñ ïîäàííûìè óïðàâëÿþùèìè ñèãíàëàìè è íå çàâèñÿò îò
ïðåäûäóùèõ ñèãíàëîâ. Ìåòîäû ñèíòåçà öèôðîâûõ óñòðîéñòâ îñíîâàíû íà èñïîëüçîâàíèè ïîëîæåíèé àëãåáðû ëîãèêè, èçëîæåííûõ
â ïåðâîì ðàçäåëå ïîñîáèÿ.
 øåñòîé ãëàâå ðàññìàòðèâàþòñÿ îñíîâíûå ëîãè÷åñêèå ýëåìåíòû, ñ ïîìîùüþ êîòîðûõ ñèíòåçèðóþòñÿ ÊÖÓ. Çäåñü ïðèâîäÿòñÿ
òîëüêî ñàìûå îáùèå ïàðàìåòðû ëîãè÷åñêèõ ýëåìåíòîâ áåç èõ ñõåìíûõ ïîäðîáíîñòåé. Òàêæå â ýòîé ãëàâå äåìîíñòðèðóåòñÿ âîçìîæíîñòü âçàèìíîé çàìåíû ëîãè÷åñêèõ ýëåìåíòîâ, ïðèâîäÿòñÿ ïðèìåðû ôóíêöèîíàëüíî ïîëíûõ ëîãè÷åñêèõ ýëåìåíòîâ, óïîìèíàþòñÿ ýëåìåíòû È ÈËÈ è È ÈËÈ ÍÅ.
8
Ñåäüìàÿ ãëàâà ïîñâÿùåíà èçó÷åíèþ ìåòîäèêè àíàëèçà è ñèíòåçà êîìáèíàöèîííûõ öèôðîâûõ óñòðîéñòâ íà îñíîâå ïðåîáðàçîâàòåëÿ êîäà Ãðåÿ â íàòóðàëüíûé äâîè÷íûé êîä. Çäåñü ðàññìîòðåíû
ìåðû, ïîçâîëÿþùèå óñòðàíÿòü ýôôåêò ãîíîê; ñèíòåç ôîðìèðîâàòåëÿ è ïðèåìíîãî óñòðîéñòâà êîäà ñ ïðîâåðêîé íà ÷åòíîñòü, ïîçâîëÿþùåãî îáíàðóæèâàòü îäèíî÷íûå îøèáêè, à òàêæå øèôðàòîðà è äåøèôðàòîðà êîäà Õýììèíãà, èñïðàâëÿþùåãî îäèíî÷íûå
îøèáêè.
Øèôðàòîðû è äåøèôðàòîðû â óçêîì çíà÷åíèè ýòèõ ïîíÿòèé,
ò. å. êàê ïðåîáðàçîâàòåëè êîäà «1 èç m» â íàòóðàëüíûé äâîè÷íûé è
îáðàòíî, èçó÷àþòñÿ â âîñüìîé ãëàâå, ãäå òàêæå ðàññìàòðèâàþòñÿ
íàçíà÷åíèå è ïðèìåíåíèå ïðèîðèòåòíûõ øèôðàòîðîâ.
Ñâåäåíèÿ î ìóëüòèïëåêñîðàõ è äåìóëüòèïëåêñîðàõ è èõ ïðèìåíåíèè èçëîæåíû â äåâÿòîé ãëàâå.
 äåñÿòîé ãëàâå ðàññìîòðåíû îäíî- è ìíîãîðàçðÿäíûå àðèôìåòè÷åñêèå è àëãåáðàè÷åñêèå ñóììàòîðû, ïðåäñòàâëåííûå â ôîðìàòå ñ ôèêñèðîâàííîé è ïëàâàþùåé çàïÿòûìè, ïðèâåäåíû êðàòêèå
ñâåäåíèÿ îá àðèôìåòè÷åñêèõ óìíîæèòåëÿõ.
 îäèííàäöàòîé ãëàâå ñèíòåçèðóþòñÿ îäíî- è ìíîãîðàçðÿäíûå
êîìïàðàòîðû, ïîêàçàíû ñïîñîáû íàðàùèâàíèÿ ðàçðÿäíîñòè è
ïðèâåäåíû ïðèìåðû èõ èñïîëüçîâàíèÿ.
Äâåíàäöàòàÿ ãëàâà ïîñâÿùåíà âîçìîæíîñòè ðåàëèçàöèè êîìáèíàöèîííûõ öèôðîâûõ óñòðîéñòâ íà îñíîâå ïðîãðàììèðóåìûõ
èíòåãðàëüíûõ ñõåì. Îñîáîå âíèìàíèå çäåñü óäåëåíî ïåðñïåêòèâíûì â íàñòîÿùåå âðåìÿ ïðîãðàììèðóåìûì ëîãè÷åñêèì èíòåãðàëüíûì ñõåìàì (ÏËÈÑ).
 òðåòüåì ðàçäåëå ïîñëå îáùèõ ñâåäåíèé, ïðèâåäåííûõ â ãë. 13,
ðàññìîòðåíû âî âñåì èõ ðàçíîîáðàçèè íàèáîëåå âàæíûå ïîñëåäîâàòåëüíîñòíûå öèôðîâûå óñòðîéñòâà, òàêèå êàê òðèããåðû (ãë. 14),
ñ÷åò÷èêè (ãë. 15) è ðåãèñòðû (ãë. 16).
 ÷åòâåðòîì ðàçäåëå îïèñàíû ìèêðîïðîöåññîðû: èõ êëàññèôèêàöèÿ è àðõèòåêòóðà (ãë. 17), ñèñòåìû êîìàíä (ãë. 18), øèííûå
ïðèåìîïåðåäàò÷èêè (ãë. 19), ñòðóêòóðà è îñíîâíûå ýëåìåíòû àðèôìåòèêî-ëîãè÷åñêîãî óñòðîéñòâà (ãë. 20), äàíû ñâåäåíèÿ î ðàçðàáîòêå ïðîãðàììíîãî îáåñïå÷åíèÿ (ãë. 21), ìèêðîêîíòðîëëåðàõ (ãë. 22)
è íåêîòîðûõ ôóíêöèîíàëüíûõ óçëàõ ìèêðîïðîöåññîðíûõ ñèñòåì
(ãë. 23).
 êîíöå êàæäîé ãëàâû ïðåäëàãàþòñÿ êîíòðîëüíûå âîïðîñû è
óïðàæíåíèÿ.
9
ÂÂÅÄÅÍÈÅ
 íàñòîÿùåå âðåìÿ ïðàêòè÷åñêè âî âñåõ ðàäèîòåõíè÷åñêèõ óñòðîéñòâàõ è ñèñòåìàõ èñïîëüçóåòñÿ öèôðîâàÿ òåõíèêà. Ýòî ñâÿçàíî
ñ öåëûì ðÿäîì ïðåèìóùåñòâ öèôðîâûõ ñèãíàëîâ ïåðåä àíàëîãîâûìè è, â ïåðâóþ î÷åðåäü, ñ òî÷íîñòüþ, ïîìåõîóñòîé÷èâîñòüþ è
âîçìîæíîñòüþ õðàíåíèÿ èíôîðìàöèè. Óòî÷íèì íåêîòîðûå îñíîâíûå îïðåäåëåíèÿ è ïîíÿòèÿ, èñïîëüçóÿ ýíöèêëîïåäè÷åñêèé [6] è
òîëêîâûå ñëîâàðè [10, 32].
Öèôðû (îò ïîçäíåëàòèíñêîãî cifra) çíàêè äëÿ îáîçíà÷åíèÿ
÷èñåë. Ïåðâûå öèôðû ïîÿâèëèñü ó åãèïòÿí è âàâèëîíÿí. Ó ðÿäà
íàðîäîâ (äðåâíèõ ãðåêîâ, ôèíèêèÿí, åâðååâ, ñèðèéöåâ) öèôðàìè ñëóæèëè áóêâû àëôàâèòà, ÷òî ñîõðàíèëîñü ÷àñòè÷íî â øåñòíàäöàòåðè÷íîé ñèñòåìå ñ÷èñëåíèÿ; àíàëîãè÷íàÿ ñèñòåìà äî XVI â.
ïðèìåíÿëàñü è â Ðîññèè. Â ñðåäíèå âåêà â Åâðîïå ïîëüçîâàëèñü
ñèñòåìîé ðèìñêèõ öèôð (I, II, III, IV, V, VI è ò. ä.), îñíîâàííîé
íà óïîòðåáëåíèè îñîáûõ çíàêîâ äëÿ äåñÿòè÷íûõ ðàçðÿäîâ I = 1,
X = 10, C = 100, M = 1000 è èõ ïîëîâèí V = 5, L = 50, D = 500.
Ñîâðåìåííûå öèôðû (àðàáñêèå), ïåðåíåñåííûå â Åâðîïó àðàáàìè â XIII â. (ïî-âèäèìîìó, èç Èíäèè), ïîëó÷èëè øèðîêîå ðàñïðîñòðàíåíèå âî âòîðîé ïîëîâèíå XV â.  óçêîì ñìûñëå ñëîâà öèôðàìè íàçûâàþòñÿ çíàêè: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Ñ÷èñëåíèå (íóìåðàöèÿ) âûðàæåíèå è îáîçíà÷åíèå ÷èñåë.
 ðàçâèòûõ ñèñòåìàõ ñ÷èñëåíèÿ íåêîòîðîå ÷èñëî n åäèíèö (íàïðèìåð, äåñÿòü) îáúåäèíÿåòñÿ â îäíó åäèíèöó 2-ãî ðàçðÿäà (äåñÿòîê), òî æå ÷èñëî åäèíèö 2-ãî ðàçðÿäà îáúåäèíÿåòñÿ â åäèíèöó
3-ãî ðàçðÿäà (ñîòíþ) è ò. ä.
×èñëî åäèíèö n íàçûâàåòñÿ îñíîâàíèåì ñèñòåìû ñ÷èñëåíèÿ, à
çíàêè, óïîòðåáëÿåìûå äëÿ îáîçíà÷åíèÿ êîëè÷åñòâà åäèíèö êàæäîãî ðàçðÿäà, öèôðàìè. Íàèáîëåå ïðèìåíÿåìàÿ ñèñòåìà ñ÷èñëåíèÿ äåñÿòè÷íàÿ, ñ öèôðàìè 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ïðîèñõîæäåíèå äåñÿòè÷íîé ñèñòåìû ñ÷èñëåíèÿ ñâÿçàíî ñ ïàëüöåâûì
ñ÷åòîì. Íåêîòîðûå íàðîäû ïîëüçîâàëèñü ïÿòåðè÷íîé ñèñòåìîé ñ÷èñëåíèÿ; â Äðåâíåì Âàâèëîíå áûëà ðàñïðîñòðàíåíà øåñòèäåñÿòåðè÷íàÿ ñèñòåìà, ñëåäû êîòîðîé ñîõðàíèëèñü â äåëåíèè ÷àñà è ãðàäóñà íà 60 ìèíóò è ìèíóòû íà 60 ñåêóíä.
 ýëåêòðîííûõ âû÷èñëèòåëüíûõ ìàøèíàõ (ÝÂÌ) ïðèìåíÿåòñÿ
äâîè÷íàÿ ñèñòåìà ñ÷èñëåíèÿ, â êîòîðîé êàæäîå ÷èñëî âûðàæàåòñÿ
10
ïðè ïîìîùè äâóõ öèôð 0 è 1. Â ñïåöèàëèçèðîâàííûõ ýëåêòðîííûõ
öèôðîâûõ óñòðîéñòâàõ èíîãäà èñïîëüçóþòñÿ êîìáèíèðîâàííûå (ñìåøàííûå) ñèñòåìû, â êîòîðûõ êàæäûé ðàçðÿä èìååò ñâîé èíäèâèäóàëüíûé âåñîâîé êîýôôèöèåíò. Íàïðèìåð, â êîäå 321 ñòàðøèé
ðàçðÿä èìååò âåñîâîé ìíîæèòåëü 3, ñðåäíèé 2 è ìëàäøèé 1.
Óñòðîéñòâî êîíñòðóêòèâíî çàêîí÷åííîå òåõíè÷åñêîå ñðåäñòâî, èìåþùåå îïðåäåëåííîå ôóíêöèîíàëüíîå íàçíà÷åíèå.
Öèôðîâîå óñòðîéñòâî (ÖÓ) îáðàáàòûâàåò öèôðîâûå âîçäåéñòâèÿ
ðàçëè÷íîé ôèçè÷åñêîé ïðèðîäû.
Ïåðâûå àðèôìåòè÷åñêèå ÖÓ áûëè ïîçèöèîííîãî òèïà ìåõàíè÷åñêîãî äåéñòâèÿ è íàçûâàëèñü àáàêè (îò ãðå÷. àbax äîñêà).
Àáàê äîñêà, ðàçäåëåííàÿ íà ïîëîñû, ãäå ïåðåäâèãàëèñü êàìåøêè, êîñòè (êàê â ðóññêèõ ñ÷åòàõ), èñïîëüçîâàëàñü äëÿ àðèôìåòè÷åñêèõ âû÷èñëåíèé â Äðåâíåé Ãðåöèè, Ðèìå, à çàòåì è â Çàïàäíîé Åâðîïå äî XVIII â.
 50-å ãîäû XX â. åùå øèðîêî ïðèìåíÿëèñü àðèôìîìåòðû «Ôåëèêñ» ìåõàíè÷åñêîãî òèïà è íà÷èíàëè ïðèìåíÿòüñÿ êëàâèøíûå è
ñ÷åòíî-ïåðôîðàöèîííûå ìàøèíû íà ýëåêòðîííûõ ëàìïàõ.
Èñêëþ÷èòåëüíî âàæíîå çíà÷åíèå äëÿ âñåãî ïîñëåäóþùåãî ðàçâèòèÿ ýëåêòðîííûõ öèôðîâûõ óñòðîéñòâ èìåëî îòêðûòèå, ñäåëàííîå â 1918 ã. ñîâåòñêèì ó÷åíûì Ì. À. Áîí÷-Áðóåâè÷åì, îáíàðóæèâøèì, ÷òî íàïðÿæåíèå è òîê â àïåðèîäè÷åñêîì óñèëèòåëå ñ
çàìêíóòîé ïåòëåé ïîëîæèòåëüíîé îáðàòíîé ñâÿçè ïðèîáðåòàþò ñïîñîáíîñòü ê ñêà÷êàì (ðåãåíåðàòèâíûì ïðîöåññàì, ò. å. î÷åíü áûñòðûì èçìåíåíèÿì). Èçîáðåòåííîå èì ñïóñêîâîå óñòðîéñòâî, â êîòîðîì èñïîëüçîâàëîñü ýòî îòêðûòèå, ÿâèëîñü îñíîâîé äëÿ ïîëó÷èâøèõ øèðîêîå ïðèìåíåíèå â ðàçëè÷íûõ îáëàñòÿõ òåõíèêè (â
òîì ÷èñëå è âû÷èñëèòåëüíîé) âñÿêîãî ðîäà ðåëå (òðèããåðîâ) è
ðåëàêñàöèîííûõ ãåíåðàòîðîâ (ìóëüòèâèáðàòîðîâ è äðóãèõ óñòðîéñòâ).
 öèôðîâîé âû÷èñëèòåëüíîé òåõíèêå èñïîëüçóþòñÿ öèôðîâûå
ñèãíàëû, êîòîðûå â ïðîìåæóòêàõ ìåæäó áûñòðûìè ïåðåïàäàìè
ïðèíèìàþò ëèøü îïðåäåëåííûå êâàíòîâàííûå çíà÷åíèÿ.  áîëåå
óçêîì ñìûñëå ñëîâà, áûñòðûå ïåðåïàäû öèôðîâûõ ñèãíàëîâ äîëæíû ïðîèñõîäèòü â ñòðîãî îïðåäåëåííûå ìîìåíòû âðåìåíè, çàäàííûå ñèñòåìîé ñèíõðîíèçàöèè.
Äâîè÷íûé öèôðîâîé ñèãíàë èìååò äâà ôèêñèðîâàííûõ óðîâíÿ, óñëîâíî îáîçíà÷àåìûå íóëåì x 0 è åäèíèöåé x1, ðàçäåëåííûå
ìåæäó ñîáîé ïîðîãîâûì óðîâíåì xïîð.
Ðàçëè÷àþò ïîòåíöèàëüíîå è èìïóëüñíîå êîäèðîâàíèå. Ïðè ïîòåíöèàëüíîì êîäèðîâàíèè ñèãíàë, ïðåâûøàþùèé ïîðîãîâûé óðîâåíü (x > xïîð), îáîçíà÷àåòñÿ ëîãè÷åñêîé åäèíèöåé (ëîã. 1), à ñèãíàë,
êîòîðûé íèæå ïîðîãîâîãî óðîâíÿ (x < xïîð) îáîçíà÷àåòñÿ ëîãè÷åñêèì íóëåì (ëîã. 0).
Ïðè èìïóëüñíîì êîäèðîâàíèè ñóùåñòâåííûì ÿâëÿåòñÿ íå àáñîëþòíûé óðîâåíü ñèãíàëà, à çíàê (íàïðàâëåíèå) ïåðåïàäà. Åñëè
11
ïðèíÿòî, ÷òî ðàáîòà ïðîèñõîäèò ïî ïîëîæèòåëüíîìó ïåðåïàäó,
ôðîíò èìïóëüñà êîäèðóåòñÿ ëîãè÷åñêîé åäèíèöåé, à âñÿ îñòàëüíàÿ ÷àñòü ñèãíàëà ëîãè÷åñêèì íóëåì. Ïðè ðàáîòå ïî îòðèöàòåëüíîìó ïåðåïàäó ñðåç èìïóëüñà êîäèðóåòñÿ ëîãè÷åñêîé åäèíèöåé, à âñå îñòàëüíîå ëîãè÷åñêèì íóëåì.
Òàêèì îáðàçîì, êîäèðîâàíèå öèôðîâîãî ñèãíàëà èíôîðìàöèîííûìè (ëîãè÷åñêèìè) ñèìâîëàìè ÿâëÿåòñÿ óñëîâíûì è òðåáóåò
îáÿçàòåëüíîé îãîâîðêè.
Öèôðîâàÿ âû÷èñëèòåëüíàÿ ìàøèíà (ÖÂÌ) âûïîëíÿåò ïî çàäàííîé ïðîãðàììå îáðàáîòêó èíôîðìàöèè, ïðåäñòàâëåííîé â öèôðîâîé ôîðìå. Êàæäîé öèôðå â ÖÂÌ ñîîòâåòñòâóåò îäèí èëè íåñêîëüêî äèñêðåòíûõ ñèãíàëîâ, íàïðèìåð ýëåêòðè÷åñêèõ èìïóëüñîâ. Ïðîöåññ îáðàáîòêè èíôîðìàöèè íà ÖÂÌ ñâîäèòñÿ ê òàêîìó
ïðåîáðàçîâàíèþ ñèãíàëîâ, ïðè êîòîðîì ðåçóëüòèðóþùèé ñèãíàë
÷èñëåííî ðàâåí èòîãó ñîîòâåòñòâóþùåé âû÷èñëèòåëüíîé îïåðàöèè. Ïðèíöèïèàëüíî ÖÂÌ ñîñòîèò èç ñëåäóþùèõ óñòðîéñòâ: àðèôìåòè÷åñêîãî, ïàìÿòè, óïðàâëåíèÿ è ââîäà-âûâîäà äàííûõ.
Áëîê ÖÂÌ, êîòîðûé óïðàâëÿåò åå ðàáîòîé, íàçûâàåòñÿ ïðîöåññîðîì. Ïðîöåññîð, ñîçäàííûé íà îñíîâå èíòåãðàëüíîé ìèêðîñõåìû, íàçûâàåòñÿ ìèêðîïðîöåññîðîì (ÌÏ).
Èçîáðåòåíèå òðàíçèñòîðà Ä. Áàðäèíûì, Ó. Áðàòòåéíîì è
Ó. Øîêëè (ÑØÀ) â êîíöå 40-õ ãîäîâ XX â. ïðîèçâåëî ðåâîëþöèîííîå äåéñòâèå â ýëåêòðîíèêå, ðàäèîòåõíèêå è âû÷èñëèòåëüíîé
òåõíèêå. Ïîëóïðîâîäíèêîâûå ïðèáîðû, èìåþùèå çíà÷èòåëüíî
ìåíüøèå ãàáàðèòû è ìàññû, ÷åì ðàäèîëàìïû, îáóñëîâèëè ïîâûøåíèå íàäåæíîñòè ðàáîòû ðàäèîàïïàðàòóðû, ñ÷åòíî-ìàòåìàòè÷åñêèõ ìàøèí è äðóãèõ óñòàíîâîê.
 ðàäèîòåõíèêå öèôðîâûå âû÷èñëèòåëüíûå óñòðîéñòâà îáåñïå÷èâàþò:
1) ôîðìèðîâàíèå è îáðàáîòêó ñèãíàëîâ â ñèñòåìàõ ðàäèîëîêàöèè, òåëåâèäåíèÿ, ðàäèîíàâèãàöèè, ðàäèîóïðàâëåíèÿ, ïåðåäà÷è
èíôîðìàöèè;
2) ìîäåëèðîâàíèå ðåàëüíûõ ðàäèîòåõíè÷åñêèõ óñòðîéñòâ, ñèñòåì è êîìïëåêñîâ;
3) àíàëèç è îïòèìèçàöèþ õàðàêòåðèñòèê îòäåëüíûõ óñòðîéñòâ
(íàïðèìåð, ðàñïðåäåëåíèÿ ýëåêòðîìàãíèòíîãî ïîëÿ â áëèæíåé çîíå
ðàñêðûâà àíòåííû);
4) ðàáîòó ñèñòåì àâòîìàòèçèðîâàííîãî ïðîåêòèðîâàíèÿ.
Âñå ïåðå÷èñëåííûå çàäà÷è, çà èñêëþ÷åíèåì ïåðâîé, ðåøàþòñÿ
ñ ïîìîùüþ óíèâåðñàëüíûõ öèôðîâûõ âû÷èñëèòåëüíûõ ìàøèí. ×òî
êàñàåòñÿ ïåðâîé çàäà÷è, êàê ïðàâèëî, îíà ðåøàåòñÿ ïóòåì èñïîëüçîâàíèÿ êàê ñïåöèàëèçèðîâàííûõ öèôðîâûõ âû÷èñëèòåëüíûõ óñòðîéñòâ (ñèíõðîíèçàòîðîâ, ôîðìèðîâàòåëåé çîíäèðóþùèõ øèðîêîïîëîñíûõ ñèãíàëîâ, àíàëîãî-öèôðîâûõ è öèôðîàíàëîãîâûõ ïðåîáðàçîâàòåëåé, óñòðîéñòâ ïåðâè÷íîé ïî îäíîìó öèêëó îáçîðà îáðàáîòêè èíôîðìàöèè, ò. å. óñòðîéñòâ îáíàðóæåíèÿ è îöåíêè ïàðà12
ìåòðîâ ñèãíàëà), òàê è óíèâåðñàëüíûõ (îò ìèêðî- äî áîëüøèõ
ÝÂÌ).
Âñå ïðîáëåìû âû÷èñëèòåëüíîé òåõíèêè ñêëàäûâàþòñÿ èç òðåõ
îñíîâíûõ êîìïîíåíòîâ: ñîçäàíèÿ ýëåìåíòíîé áàçû; ðàçðàáîòêè
ñàìèõ ÝÂÌ è ïðîãðàììíîãî îáåñïå÷åíèÿ ê íèì; ýêîíîìè÷åñêè
âûãîäíîãî èñïîëüçîâàíèÿ âû÷èñëèòåëüíîé òåõíèêè â íàðîäíîì
õîçÿéñòâå.
Ñëåäóåò îòìåòèòü, ÷òî ðåçêîå èçìåíåíèå ýëåìåíòíîé áàçû ïóòåì ïåðåõîäà îò ñõåì íà äèñêðåòíûõ ýëåìåíòàõ ê èíòåãðàëüíûì
ìèêðîñõåìàì ðàçëè÷íîé ñòåïåíè èíòåãðàöèè ïðèâåëî ê êà÷åñòâåííîìó ñêà÷êó â îáëàñòè èíæåíåðíûõ ìåòîäîâ ñèíòåçà öèôðîâûõ
âû÷èñëèòåëüíûõ óñòðîéñòâ íà èõ îñíîâå.
Ïîíèìàíèå ðàáîòû öèôðîâûõ óñòðîéñòâ, à òåì áîëåå èõ ðàçðàáîòêà, íåâîçìîæíû áåç ãëóáîêîãî çíàíèÿ îñíîâ àëãåáðû ëîãèêè.
Àëãåáðà ëîãèêè ñèñòåìà àëãåáðàè÷åñêèõ ìåòîäîâ ðåøåíèÿ ëîãè÷åñêèõ çàäà÷; â óçêîì ñìûñëå ýòî òàáëè÷íîå, ìàòðè÷íîå ïîñòðîåíèå ëîãèêè âûñêàçûâàíèé, îïðåäåëÿþùåå ëîãè÷åñêèå îïåðàöèè íàä íèìè.
Èñòîðè÷åñêèå êîðíè àëãåáðû ëîãèêè îáíàðóæèâàþòñÿ â Äðåâíåé Ãðåöèè è ñâÿçàíû â ïåðâóþ î÷åðåäü ñ èìåíåì ôèëîñîôà Ãåðàêëèòà (êîíåö VI íà÷àëî V ââ. äî í. ý.), îäíîãî èç îñíîâàòåëåé
äèàëåêòèêè.
Çàêîí, êîòîðûì ñâÿçàíî âñÿêîå èçìåíåíèå è äâèæåíèå, Ãåðàêëèò íàçûâàåò Ëîãîñîì (îò ãðå÷. logos ðå÷ü, ñëîâî, ðàçóìíîå îñíîâàíèå). Ýòîò òåðìèí âïåðâûå ââîäèòñÿ â ôèëîñîôèþ Ãåðàêëèòîì äëÿ îáîçíà÷åíèÿ çàêîíîìåðíîñòåé ñâÿçè âåùåé [5].
Äèàëåêòèêà (îò ãðå÷. dialektike èñêóññòâî âåñòè áåñåäó, ñïîð)
ýòî ôèëîñîôñêîå ó÷åíèå î ñòàíîâëåíèè è ðàçâèòèè áûòèÿ è ïîçíàíèÿ è îñíîâàííûé íà ýòîì ó÷åíèè ìåòîä ìûøëåíèÿ.  èñòîðèè
ôèëîñîôèè âûäâèãàëèñü ðàçëè÷íûå òîëêîâàíèÿ äèàëåêòèêè: êàê
ó÷åíèÿ î âå÷íîì ñòàíîâëåíèè è èçìåí÷èâîñòè áûòèÿ (Ãåðàêëèò);
èñêóññòâà äèàëîãà, äîñòèæåíèÿ èñòèíû ïóòåì ïðîòèâîáîðñòâà ìûñëåé (Ñîêðàò, 470 399 ãã. äî í. ý.); ìåòîäà ðàñ÷ëåíåíèÿ è ñâÿçûâàíèÿ ïîíÿòèé ñ öåëüþ ïîñòèæåíèÿ ñâåðõ÷óâñòâåííîé (èäåàëüíîé)
ñóùíîñòè âåùåé (Ïëàòîí, 428/427 348/347 ãã. äî í. ý.) è äð. [6].
Àëãåáðà (àðàáñêîå ñëîâî) ÷àñòü ìàòåìàòèêè, ñâÿçàííàÿ ñ ðåøåíèåì àëãåáðàè÷åñêèõ óðàâíåíèé (ïðèðàâíèâàíèåì äâóõ àëãåáðàè÷åñêèõ âûðàæåíèé).  ñîâðåìåííîé àëãåáðå èçó÷àþòñÿ àëãåáðàè÷åñêèå îïåðàöèè, àíàëîãè÷íûå äåéñòâèÿì íàä ÷èñëàìè. Òàêèå îïåðàöèè ìîãóò âûïîëíÿòüñÿ íàä ìíîãî÷ëåíàìè, âåêòîðàìè, ìàòðèöàìè è ò. ä.
Àëãåáðàè÷åñêîå âûðàæåíèå ñîñòàâëÿåòñÿ èç áóêâ è ÷èñåë, ñîåäèíåííûõ èëè îòìå÷åííûõ çíàêàìè àëãåáðàè÷åñêèõ äåéñòâèé è çíàêàìè ïîñëåäîâàòåëüíîñòè âûïîëíåíèÿ ýòèõ äåéñòâèé.
Ëîãèêà (îò ãðå÷. logike) íàóêà î ñïîñîáàõ äîêàçàòåëüñòâ è
îïðîâåðæåíèé; ñîâîêóïíîñòü íàó÷íûõ òåîðèé, â êàæäîé èç êî13
òîðûõ ðàññìàòðèâàþòñÿ îïðåäåëåííûå ñïîñîáû äîêàçàòåëüñòâ è
îïðîâåðæåíèé. Îñíîâàòåëåì ëîãèêè ñ÷èòàåòñÿ ó÷åíèê Ïëàòîíà,
äðåâíåãðå÷åñêèé ôèëîñîô è ó÷åíûé Àðèñòîòåëü1 (384 322 ãã.
äî í. ý.).
Ñèëëîãèñòèêà (îò ãðå÷. syllogistikos âûâîäÿùèé óìîçàêëþ÷åíèå) èñòîðè÷åñêè ïåðâîå, ñîçäàííîå Àðèñòîòåëåì ó÷åíèå î
ëîãè÷åñêîé äåäóêöèè, â êîòîðîì ðàññìàòðèâàþòñÿ ðàññóæäåíèÿ â
ôîðìå ñèëëîãèçìîâ.
×òîáû îòëè÷èòü ëîãè÷åñêèå ôîðìû îò ñîäåðæàíèÿ è ëîãè÷åñêèå êîíñòàíòû îò ëîãè÷åñêèõ ïåðåìåííûõ, Àðèñòîòåëü ïåðâûé ââåë
ñïåöèàëüíûå îáîçíà÷åíèÿ äëÿ òåõ è äðóãèõ: ëîãè÷åñêèå êîíñòàíòû îí îáîçíà÷àë ñëîâåñíî, à ëîãè÷åñêèå ïåðåìåííûå áóêâàìè
ãðå÷åñêîãî àëôàâèòà2.
 êà÷åñòâå ïðèìåðà ìîæíî ïðèâåñòè âûðàæåíèå ïåðâîé ôèãóðû ñèëëîãèçìà: «Åñëè À ñêàçûâàåòñÿ î âñÿêîì Â, à  ñêàçûâàåòñÿ î
âñÿêîì Ã, òî À íåîáõîäèìî ñêàçûâàåòñÿ î âñÿêîì û. Çäåñü ñëîâàìè «åñëè ..., òî» è «ñêàçûâàåòñÿ î âñÿêîì» âûðàæàþòñÿ ëîãè÷åñêèå êîíñòàíòû ñëåäîâàíèÿ è ñóæäåíèÿ, ò. å. ëîãè÷åñêèå ñâÿçè çàêîí÷åííûõ ìûñëåé äðóã ñ äðóãîì è ýëåìåíòîâ îòäåëüíûõ çàêîí÷åííûõ ìûñëåé ïîñûëîê, à áóêâàìè ãðå÷åñêîãî àëôàâèòà îáîçíà÷àþòñÿ ëîãè÷åñêèå ïåðåìåííûå, äîïóñêàþùèå ïîäñòàíîâêó íà
èõ ìåñòî îïðåäåëåííûõ òåðìèíîâ [5].
1
Àðèñòîòåëü ðîäèëñÿ â 384 ã. äî í. ý. â Ñòàãèðå ãðå÷åñêîé êîëîíèè íà Ôðàêèéñêîì ïîáåðåæüå. Åãî îòåö Íèêîìàõ áûë ïðèäâîðíûì âðà÷îì è äðóãîì ìàêåäîíñêîãî öàðÿ Àìèíòû II.  343 ã. ìàêåäîíñêèé öàðü Ôèëèïï ïðèãëàøàåò Àðèñòîòåëÿ çàíÿòüñÿ âîñïèòàíèåì ñâîåãî ñûíà Àëåêñàíäðà (áóäóùåãî Àëåêñàíäðà Ìàêåäîíñêîãî), êîòîðîìó òîãäà èñïîëíèëîñü 13 ëåò. Àðèñòîòåëü îòïðàâëÿåòñÿ â Ïåëëó, ãäå è ðóêîâîäèò âîñïèòàíèåì Àëåêñàíäðà áîëåå òðåõ ëåò. Ïîñëå òîãî êàê
Àëåêñàíäð ñòàë öàðåì, Àðèñòîòåëü ïåðååõàë â ñâîé ðîäíîé ãîðîä Ñòàãèð, à â 335 ã.
âåðíóëñÿ ñíîâà â Àôèíû.  ïðåäìåñòüå Àôèí Ëèêåå (Ëèöåå) îêîëî õðàìà Àïîëëîíà Ëèêåéñêîãî îí ñîçäàåò ñâîþ ñîáñòâåííóþ øêîëó.  ýòîò ïåðèîä ó Àðèñòîòåëÿ ñîçðåâàåò êðèòè÷åñêîå îòíîøåíèå ê ó÷åíèþ Ïëàòîíà (â ÷àñòíîñòè, ê ó÷åíèþ
îá èäåÿõ) [6]. Íåîáõîäèìî çàìåòèòü, ÷òî ñî÷èíåíèÿ Àðèñòîòåëÿ îõâàòûâàþò âñå
îáëàñòè òîãäàøíèõ çíàíèé.
Àðèñòîòåëü âèäåë ñâîþ çàñëóãó ãëàâíûì îáðàçîì â òîì, ÷òî îí îòêðûë ñèëëîãèçì, êîòîðûé åñòü ïðåæäå âñåãî ñðåäñòâî äîêàçûâàíèÿ îáúåêòèâíîé èñòèíû.
Ëîãèêà Àðèñòîòåëÿ îñíîâàíà íà îáúåêòèâíîì ðàçëè÷åíèè èñòèíû è ëæè (îò
ãðå÷. pseudos ïñåâäî). Èñòèíà ïîíèìàåòñÿ Àðèñòîòåëåì ìàòåðèàëèñòè÷åñêè
êàê ñîîòâåòñòâèå óòâåðæäåíèÿ èëè îòðèöàíèÿ áûòèÿ, äåéñòâèòåëüíîñòè, íåçàâèñèìîé îò ñîçíàíèÿ, à ëîæü êàê íåñîîòâåòñòâèå.
Èíäóêöèÿ ïî Àðèñòîòåëþ ýòî òà æå ñèëëîãèñòè÷åñêàÿ ñâÿçü, íî â îáðàòíîì
ïîðÿäêå: ýòî íå âûâîä ÷åðåç çíàíèå ïðè÷èíû èëè ñëåäñòâèÿ, à âûâîä î ïðè÷èíå
è ñëåäñòâèè ÷åðåç çíàíèå íîñèòåëåé ïðè÷èíû è ñëåäñòâèÿ. Îñóùåñòâëÿåòñÿ ëè
ïîçíàíèå â íàïðàâëåíèè îò îáùåãî ê åäèíè÷íîìó (â ñèëëîãèçìå) èëè îò åäèíè÷íîãî ê îáùåìó (â èíäóêöèè), ñâÿçü ìåæäó îáùèì è åäèíè÷íûì, îïðåäåëÿþùèì è îïðåäåëÿåìûì îñòàåòñÿ îäíîé è òîé æå.
2
Áóêâû, óïîòðåáëÿåìûå Àðèñòîòåëåì ïåðâîíà÷àëüíî äëÿ ñîêðàùåíèÿ ñëîâ
(âïîñëåäñòâèè èõ ñòàëè íàçûâàòü àááðåâèàòóðîé), ïîçæå ñòàëè èñïîëüçîâàòüñÿ èì
â êà÷åñòâå íàñòîÿùèõ ëîãè÷åñêèõ ïåðåìåííûõ.
14
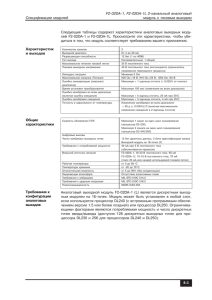
 ñîîòâåòñòâèè ñ ó÷åíèåì î I
ñóæäåíèè êàê óòâåðæäåíèè èëè
x1x2x3
îòðèöàíèè Àðèñòîòåëü ðàçëè÷àåò â ñóæäåíèè äâà ýëåìåíòà: ïîäx1x2x3 x1x2x3
x1x2x3
ëåæàùåå òî, îòíîñèòåëüíî
÷åãî ÷òî-òî ñêàçûâàåòñÿ, ðàçóìåÿ
ïîä ïîäëåæàùèì òî, íà ÷òî íàx1x2x3
x1x2x3
ïðàâëåíà ìûñëü, è ñêàçóåìîå,
ò. å. âñå òî, ÷òî óòâåðæäàåòñÿ èëè
x1x2x3
x1x2x3
îòðèöàåòñÿ [5].
Âïîñëåäñòâèè Áîýöèé1 îáúåäèíèë âñå âîçìîæíûå ÷åòûðå
Ðèñ. Â.1. Äèàãðàììà Ýéëåðà
ñëó÷àÿ îòðèöàíèÿ ÷ëåíîâ ñîåäèíåíèÿ êîííåêñèè (îòðèöàíèå îòñóòñòâèÿ äâóõ ÷ëåíîâ êîííåêñèè;
îòðèöàíèå ñîñóùåñòâîâàíèÿ äâóõ ÷ëåíîâ êîííåêñèè; îòðèöàíèå
íàëè÷èÿ îäíîãî è îòñóòñòâèÿ äðóãîãî; îòðèöàíèå îòñóòñòâèÿ îäíîãî è íàëè÷èÿ äðóãîãî) è ñîçäàë ó÷åíèå îá ýêâèâàëåíòíîñòè ôîðì
êîííåêñèè, äèçúþíêöèè è óñëîâíîé ñâÿçè [5] ýòî òî, ÷òî òåïåðü íàçûâàþò ôîðìóëàìè Ìîðãàíà [6] 2.
Ëåîíàðä Ýéëåð3 ïðåäëîæèë èçîáðàæàòü ëîãè÷åñêèå îáúåêòû â
âèäå äèàãðàìì (ðèñ. Â.1). Ñïóñòÿ áîëåå ÷åì 100 ëåò ýòî æå ïðåäëîæèë Äæîí Âåíí4. Òàêèå äèàãðàììû èëëþñòðèðóþò îòíîøåíèÿ â
àëãåáðå êëàññîâ. Åñëè ïðÿìîóãîëüíèê, êðóã, êâàäðàò è òðåóãîëüíèê îáîçíà÷åíû ñîîòâåòñòâåííî I, x1, x2, x3, òî äèàãðàììà ïîêàçûâàåò, ÷òî âñÿêàÿ ëîãè÷åñêàÿ ôóíêöèÿ îò x1, x2, x3 ìîæåò áûòü ïðåäñòàâëåíà êàê îáúåäèíåíèå ìèíèìàëüíûõ ìíîãî÷ëåíîâ (ìèíòåðìîâ) îò x1, x2, x3 [13]. Ýòî ïî ñóùåñòâó ïðåäâîñõèùàåò òåîðåìó
Êëîäà Øåííîíà5 î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé â êàíîíè÷åñêîì âèäå: â ñîâåðøåííîé äèçúþíêòèâíîé íîðìàëüíîé ôîðìå
(ÑÄÍÔ) èëè, ÷òî òî æå ñàìîå, òåîðåìó î ðàçëîæåíèè ëîãè÷åñêèõ
1
Áîýöèé (Bo¸tius) Àíèöèé Ìàíëèé Ñåâåðèí (470525) õðèñòèàíñêèé
ôèëîñîô è ðèìñêèé ãîñóäàðñòâåííûé äåÿòåëü. Ïåðåâåë íà ëàòèíñêèé ÿçûê ëîãè÷åñêèå ñî÷èíåíèÿ Àðèñòîòåëÿ è Ïîðôèðèÿ, «Àðèôìåòèêó» Íèêîìàõà, «Íà÷àëà»
Åâêëèäà.
2
Ìîðãàí (De Morgan) Îãàñòåñ (Àâãóñòóñ) (1806 1871) øîòëàíäñêèé ìàòåìàòèê è ëîãèê. Ñîçäàë òðóäû ïî àëãåáðå, òåîðèè ðÿäîâ. Íåçàâèñèìî îò Äæ. Áóëÿ
ïðèøåë ê îñíîâíûì èäåÿì ìàòåìàòè÷åñêîé ëîãèêè.
3
Ýéëåð (Euler) Ëåîíàðä (1707 1783) ìàòåìàòèê, ìåõàíèê, ôèçèê è àñòðîíîì, øâåéöàðåö ïî ïðîèñõîæäåíèþ, â 1726 ã. áûë ïðèãëàøåí â Ïåòåðáóðãñêóþ Àêàäåìèþ Íàóê è â 1727 ã. ïåðååõàë â Ðîññèþ. Âïîñëåäñòâèè àêàäåìèê Ïåòåðáóðãñêîé ÀÍ.
4
Âåíí (Venn) Äæîí (1834 1923) àíãëèéñêèé ëîãèê, ðàçðàáîòàë ãðàôè÷åñêèé àïïàðàò äèàãðàìì, ôàêòè÷åñêè ýêâèâàëåíòíûé ëîãèêå êëàññîâ. Ñîçäàë
òðóäû â îáëàñòè âåðîÿòíîñòíîé è èíäóêòèâíîé ëîãèêè.
5
Øåííîí (Shannon) Êëîä Ýëâóä (1916 2001) àìåðèêàíñêèé èíæåíåð è
ìàòåìàòèê. Îäèí èç ñîçäàòåëåé ìàòåìàòè÷åñêîé òåîðèè èíôîðìàöèè. Åãî îñíîâíûå òðóäû ïî òåîðèè ðåëåéíî-êîíòàêòíûõ ñõåì, ìàòåìàòè÷åñêîé òåîðèè ñâÿçè,
êèáåðíåòèêå.
15
ôóíêöèé â ðÿä ïî ìèíòåðìàì. Âî âòîðîé ïîëîâèíå XX â. ýòè äèàãðàììû ïðèîáðåëè ìàòðè÷íûé âèä è ñòàëè íàçûâàòüñÿ â ÷åñòü èõ
ñîçäàòåëåé êàðòàìè Êàðíî è äèàãðàììàìè Âåé÷à1.
È íàêîíåö («Last of list is not last of means!»), î Äæîðäæå Áóëå2,
îáîáùèâøåì àëãåáðó ëîãèêè, êîòîðàÿ ïîýòîìó, êàê ïðàâèëî, íàçûâàåòñÿ áóëåâîé àëãåáðîé.
Âîïðîñ î òîì, â êàêèõ îòíîøåíèÿõ íàõîäÿòñÿ ñòàðàÿ ëîãèêà è
ëîãèêà íîâàÿ, ñîâðåìåííàÿ, âñåãäà èíòåðåñîâàë èññëåäîâàòåëåé è
äî ñèõ ïîð ÿâëÿåòñÿ ïðåäìåòîì äèñêóññèé è îáñóæäåíèé. Ñ îäíîé
ñòîðîíû, ðå÷ü èäåò î òîì, êàê âïèñûâàþòñÿ â ñîâðåìåííóþ ëîãèêó ðåçóëüòàòû ìíîãîâåêîâîãî îïûòà ïî èññëåäîâàíèþ ñèëëîãèñòèêè, è íà ýòîò âîïðîñ â êàêîé-òî ìåðå îòâå÷àåò àíàëèç, ïðåäïðèíÿòûé â [7]. Ñ äðóãîé ñòîðîíû, ïðåäñòàâëÿåò èíòåðåñ è îáðàòíàÿ çàäà÷à óòî÷íåíèå òîãî, êàêàÿ ÷àñòü ñîâðåìåííîé ëîãèêè
ìîæåò áûòü îïèñàíà ñèëëîãèñòè÷åñêè. Ïðåäëàãàåìûé â [7] îòâåò
ñîñòîèò â ñëåäóþùåì: ÷òî «âñÿ ýëåìåíòàðíàÿ áóëåâà àëãåáðà îêàçûâàåòñÿ ñîäåðæàùåéñÿ â íåêîòîðîé ñèëëîãèñòè÷åñêîé òåîðèè.
À òàê êàê ýëåìåíòàðíàÿ áóëåâà àëãåáðà ýêâèâàëåíòíà îäíîìåñòíîìó ïåðâîïîðÿäêîâîìó èñ÷èñëåíèþ ïðåäèêàòîâ, òî äàííûé îòâåò
îçíà÷àåò, ÷òî îäíîìåñòíûé ôðàãìåíò èñ÷èñëåíèÿ ïðåäèêàòîâ ñîäåðæèòñÿ â ñèëëîãèñòèêå».
Êîíòðîëüíûå âîïðîñû
1. Êòî ÿâëÿåòñÿ îñíîâàòåëåì àëãåáðû ëîãèêè?
2. Ïðèâåäèòå îïðåäåëåíèå ïîíÿòèÿ àëãåáðû ëîãèêè.
3. Äàéòå îïðåäåëåíèå ïîíÿòèÿ ñèëëîãèçìà.
4. ×åì îòëè÷àåòñÿ èíäóêöèÿ îò ñèëëîãèçìà?
1
Ïðåäëàãàåòñÿ îòëè÷íèêàì ñàìîñòîÿòåëüíî ðàçãàäàòü ïðèíöèï, ïî êîòîðîìó
êàæäîìó ó÷àñòêó äèàãðàììû íà ðèñ. Â.1 ïðèñâîåíà íàäïèñü èç òðåõ áóêâ, ñ ÷åðòî÷êàìè íàä íåêîòîðûìè.
2
Áóëü (Bool ) Äæîðäæ (1815 1864) àíãëèéñêèé ìàòåìàòèê è ëîãèê, îäèí
èç îñíîâîïîëîæíèêîâ ìàòåìàòè÷åñêîé ëîãèêè, óñîâåðøåíñòâîâàâøèé åå äî ñîâðåìåííîãî ñîñòîÿíèÿ [5,7,13]. Êñòàòè, îí îòåö èçâåñòíîé ðîìàíèñòêè Ýòåëü
Ëèëèàí Âîéíè÷, àâòîðà «Îâîäà».
16
ÐÀÇÄÅË I
ÎÑÍÎÂÛ ÀËÃÅÁÐÛ ËÎÃÈÊÈ *
ÃËÀÂÀ 1
ÎÑÍÎÂÍÛÅ ÎÁÎÇÍÀ×ÅÍÈß È ÏÎÑÒÓËÀÒÛ
1.1. Îñíîâíûå âûñêàçûâàíèÿ è ïåðåìåííûå
Êàæäîå âûñêàçûâàíèå â áèíàðíîé (àðèñòîòåëåâîé) àëãåáðå
ëîãèêè ìîæåò áûòü ïðåäñòàâëåíî ïåðåìåííîé, êîòîðàÿ îáû÷íî
îáîçíà÷àåòñÿ ëàòèíñêèìè ñòðî÷íûìè áóêâàìè x èëè y. Âûñêàçûâàíèÿ ìîãóò áûòü óòâåðäèòåëüíûìè (îïðåäåëåííûìè) è íåîïðåäåëåííûìè (áåçðàçëè÷íûìè).
Óòâåðäèòåëüíûõ âûñêàçûâàíèé äâà: èñòèííîå è ëîæíîå, íåîïðåäåëåííîå òîëüêî îäíî (òàáë. 1.1).
Ñëåäóåò îòìåòèòü, ÷òî âûñêàçûâàíèÿ Ëîæü è Èñòèíà â ñîâðåìåííûõ êîìïüþòåðíûõ ïðîãðàììàõ òàêæå èñïîëüçóþòñÿ êàê
îáîçíà÷åíèÿ. Íàïðèìåð, åñëè â WinWord êóðñîðîì ìûøè â ñòðîêå ìåíþ íàæàòü êíîïêó Òàáëèöà, à çàòåì Ôîðìóëà è Âñòàâèòü
ôóíêöèþ è âûáðàòü îäíó èç ôóíêöèé: FALSE èëè TRUE, íà
ýêðàíå áóäåò íàïå÷àòàíî 0 èëè 1. Ïîïðîáóéòå ýòî ñàìè ïðîâåðèòü.
Îáîçíà÷åíèå íåîïðåäåëåííîñòè ïîêà åùå íå óñòàíîâëåíî. Ïðåäëîæåíèå èñïîëüçîâàòü â êà÷åñòâå ñèìâîëà ½ (èëè 0,5) îáîñíîâàíî
äàëåå.
Ò à á ë è ö à 1.1
Îáîçíà÷åíèå ëîãè÷åñêèõ âûñêàçûâàíèé è ïåðåìåííûõ
Âûñêàçûâàíèå
Îáîçíà÷åíèå
Ëîæü (False)
ëîã.0 (log.0); 0
Èñòèíà (True)
ëîã.1 (log.1); 1
Íåîïðåäåëåííîñòü (Uncertainty)
x, *, ½
*  çàðóáåæíûõ èçäàíèÿõ àëãåáðó ëîãèêè â ïðèìåíåíèè ê öèôðîâûì óñòðîéñòâàì íàçûâàþò àëãåáðîé ïåðåêëþ÷àòåëüíûõ ôóíêöèé (algebra of the switching
functions).
17
1.2. Îñíîâíûå ëîãè÷åñêèå îïåðàöèè
Âñåãî ëîãè÷åñêèõ îïåðàöèé òðè: îäíà óíàðíàÿ èíâåðñèÿ è äâå
áèíàðíûõ äèçúþíêöèÿ è êîíúþíêöèÿ (òàáë. 1.2).
×àùå âñåãî èíâåðñèÿ (îò ëàò. inversio ïåðåñòàíîâêà) îáîçíà), äèçúþíêöèÿ (îò ëàò. disjunctio
÷àåòñÿ ÷åðòîé íàä àðãóìåíòîì (x
ðàçîáùåíèå) çíà÷êîì ∨, à êîíúþíêöèÿ (îò ëàò. conjunctio
ñîþç, ñâÿçü) ñèìâîëîì îáû÷íîãî óìíîæåíèÿ (⋅) [6].
Ñìûñë ëîãè÷åñêèõ îïåðàöèé ðàñêðûâàåòñÿ ñ ïîìîùüþ äèàãðàìì Ýéëåðà (ðèñ. 1.1) è ïåðåáîðà âñåõ âîçìîæíûõ çíà÷åíèé àðãóìåíòîâ, íàä êîòîðûìè ïðîâîäÿòñÿ ýòè îïåðàöèè (òàáë. 1.3).
Ïðîàíàëèçèðóåì äàííûå òàáë. 1.3.
Èíâåðñèÿ. Ñîïîñòàâëåíèå ñòîëáöîâ òàáëèöû x1 ñ
x 1 è x0 ñ
x 0 ïîêàçûâàåò, ÷òî îïåðàöèþ èíâåðñèè ìîæíî âûïîëíÿòü ÷èñòî àðèôìåòè÷åñêè:
0 = 1 − 0;
1 = 1 − 1 è àëãåáðàè÷åñêè:
x = 1 − x. Îòñþäà è
âîçíèêëî åùå îäíî íàçâàíèå ýòîé îïåðàöèè äîïîëíåíèå.  ñëó÷àå
íåîïðåäåëåííîñòè (åñëè åå îáîçíà÷èòü ½), ïîëó÷èì ½ = 1 − ½ = ½,
ò. å. èíâåðñèÿ íåîïðåäåëåííîñòè ðàâíà ñàìîé íåîïðåäåëåííîñòè, ÷òî
î÷åâèäíî. Îòñþäà æå ìîæíî ñäåëàòü âûâîä, ÷òî äâîéíàÿ èíâåðñèÿ
ïðèâîäèò ê èñõîäíîìó àðãóìåíòó, ò. å.
x= 1 −
x = 1 − (1 − x) = x, è ýòî
íàçûâàåòñÿ çàêîíîì äâîéíîãî îòðèöàíèÿ.
Ò à á ë è ö à 1.2
Íàçâàíèÿ è îáîçíà÷åíèÿ ëîãè÷åñêèõ îïåðàöèé
Íàçâàíèå îïåðàöèè
Ñëîâî
Èíâåðñèÿ, îòðèöàíèå, äîïîëíåíèå
Äèçúþíêöèÿ, ëîãè÷åñêîå ñëîæåíèå,
îáúåäèíåíèå
Kîíúþíêöèÿ, ëîãè÷åñêîå óìíîæåíèå,
ïåðåñå÷åíèå
Çíàê
ÍÅ (NOT )
ÈËÈ (OR)
∨, ∪, +
È (AND)
∧, ∩, ⋅
, , ~
Ò à á ë è ö à 1.3
Òàáëèöà èñòèííîñòè ëîãè÷åñêèõ îïåðàöèé
Àðãóìåíòû
18
Ëîãè÷åñêèå îïåðàöèè
N1
N0
N1
N0
N1 ∨ N0
N1 · N0
0
0
1
1
0
0
0
1
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
1
x
x
x1 x0
x 1 x0
x1
x1 x0
x1· x 0
x1
x0
x0
à
á
â
Ðèñ. 1.1. Äèàãðàììû Ýéëåðà äëÿ îñíîâíûõ îïåðàöèé àëãåáðû ëîãèêè:
à èíâåðñèÿ; á äèçúþíêöèÿ; â êîíúþíêöèÿ
Çàêîí ëîæíîãî ïîëîæåíèÿ, ò. å. åñëè x1 = x0, òî è
x1 =
x 0, ìîæåò
áûòü äîêàçàí ñëåäóþùèì îáðàçîì. Ïîñêîëüêó 1 = 1, òî âû÷èòàÿ
èç ëåâîé è ïðàâîé åäèíèöû ðàâíûå çíà÷åíèÿ x1 è x0, ïîëó÷èì
x1 =
x 0.
1 − x1 = 1 − x0, ÷òî è ñîîòâåòñòâóåò èñêîìîìó
Äèçúþíêöèÿ.  îòëè÷èå îò îáû÷íîãî àðèôìåòè÷åñêîãî èëè àëãåáðàè÷åñêîãî ñóììèðîâàíèÿ çäåñü íàëè÷èå äâóõ åäèíèö äàåò â
ðåçóëüòàòå åäèíèöó. Èìåííî ïîýòîìó ïðè îáîçíà÷åíèè ëîãè÷åñêîãî ñóììèðîâàíèÿ íå ðåêîìåíäóåòñÿ èñïîëüçîâàòü çíàê ñëîæåíèÿ (+). Îïåðàöèåé, ýêâèâàëåíòíîé äèçúþíêöèè, ÿâëÿåòñÿ âûáîð
ìàêñèìàëüíîãî çíà÷åíèÿ èç äâóõ: MAX(x1; x0). Ýòî ñïðàâåäëèâî è
ïðè îáîçíà÷åíèè íåîïðåäåëåííîñòè ÷èñëîì ½.
Àíàëèç òàáë. 1.3 ïîçâîëÿåò ïåðåéòè ê ñîêðàùåííîé åå ôîðìå
àëãåáðàè÷åñêîé òàáëèöå èñòèííîñòè (òàáë. 1.4). Ïåðâûå äâå ñòðîêè òàáë. 1.3 (x1 = 0) îïðåäåëÿþò çàêîí ñëîæåíèÿ ñ íóëåì: x ∨ 0 = x,
à âòîðûå äâå ñòðîêè (x 1 = 1) çàêîí ñëîæåíèÿ ñ åäèíèöåé:
x ∨ 1 = 1.
Êîíúþíêöèÿ. Òàáë. 1.3 óáåäèòåëüíî ïîêàçûâàåò òîæäåñòâåííîñòü
îïåðàöèé îáû÷íîãî è ëîãè÷åñêîãî óìíîæåíèé. Ýêâèâàëåíòíîé îïåðàöèåé â äàííîì ñëó÷àå ÿâëÿåòñÿ âûáîð íàèìåíüøåãî çíà÷åíèÿ èç
äâóõ: MIN(x1; x0), ÷òî òàêæå ñïðàâåäëèâî è ïðè îáîçíà÷åíèè íåîïðåäåëåííîñòè ÷åðåç ½.  ýòîì ñëó÷àå óìåñòåí ïåðåõîä ê ñîêðàùåííîé àëãåáðàè÷åñêîé òàáë. 1.4. Ïåðâûå äâå ñòðîêè òàáë. 1.3 äîêàçûâàþò çàêîí óìíîæåíèÿ íà íóëü: x ⋅ 0 = 0 è âòîðûå äâå çàêîí óìíîæåíèÿ íà åäèíèöó: x ⋅ 1 = x.
Åùå íåñêîëüêî çàêîíîâ ìîæÒ à á ë è ö à 1.4
íî èçâëå÷ü èç àíàëèçà òàáë. 1.3,
Àëãåáðàè÷åñêàÿ òàáëèöà èñòèííîñòè
ïðèðàâíÿâ â îäíîì ñëó÷àå îáà
äèçúþíêöèè è êîíúþíêöèè
àðãóìåíòà äðóã äðóãó: x1 = x0 = x
ýòî çàêîí èäåìïîòåíòíîñòè 1,
N1
N1 ∨ N0
N1 · N0
èëè òàâòîëîãèè, à â äðóãîì ñëóN0
÷àå îäèí àðãóìåíò èíâåðñíî0
0
ìó çíà÷åíèþ äðóãîãî: x 1 =
x0
N0
1
1
(òàáë. 1.5).
1
Îò ëàò. idem òî æå ñàìîå è potente ìîãó÷èé, ìîùíûé, âëàñòü èìóùèé,
ò. å. â öåëîì, èìåþùèé òî æå ñàìîå çíà÷åíèå.
19
Ò à á ë è ö à 1.5
Çàêîíû òàâòîëîãèè è äîïîëíèòåëüíîñòè
Íàçâàíèå çàêîíà
Èäåìïîòåíòíûé, òàâòîëîãèè
Äîïîëíèòåëüíîñòè
Èñêëþ÷åííîãî òðåòüåãî
Ïðîòèâîðå÷èÿ
Äèçúþíêöèÿ
Kîíúþíêöèÿ
N∨N=N
N⋅N=N
N∨N=1
N⋅N=0
Ò à á ë è ö à 1.6
Òàáëèöà èñòèííîñòè, ïîäòâåðæäàþùàÿ çàêîííîñòü çàìåíû îïåðàöèé
èíâåðòèðîâàíèÿ, äèçúþíêöèè è êîíúþíêöèè
N1
N0
N1 ∨ N0
MAX
(N1; N0)
N1 ⋅ N0
MIN
(N1; N0)
N1
1 − N1
N0
1 − N0
0
0
0
0
0
0
1
1
1
1
0
½
½
½
0
0
1
1
½
½
0
1
1
1
0
0
1
1
0
0
½
0
½
½
0
0
½
½
1
1
½
½
½
½
½
½
½
½
½
½
½
1
1
1
½
½
½
½
0
0
1
0
1
1
0
0
0
0
1
1
1
½
1
1
½
½
0
0
½
½
1
1
1
1
1
1
0
0
0
0
Ñëåäóåò îáðàòèòü âíèìàíèå íà òî, ÷òî â òàáë. 1.5 ïðèâåäåíû
äàííûå, ñïðàâåäëèâûå òîëüêî äëÿ îïðåäåëåííûõ çíà÷åíèé ïåðåìåííîé x. Îäíàêî çàêîí òàâòîëîãèè âûïîëíÿåòñÿ òàêæå è â ñëó÷àå
íåîïðåäåëåííîãî çíà÷åíèÿ x = ½. Çàêîíû æå èñêëþ÷åííîãî òðåòüåãî è ïðîòèâîðå÷èÿ ïðè x = ½ íå äåéñòâóþò, ïîñêîëüêó íåîïðåäåëåííîñòü ñîõðàíÿåòñÿ: x ∨
x = ½ è x ⋅
x = ½.
Äëÿ äîêàçàòåëüñòâà ñïðàâåäëèâîñòè çàìåíû îïåðàöèè èíâåðñèè x íà 1 − x, äèçúþíêöèè íà îïðåäåëåíèå ìàêñèìóìà è êîíúþíêöèè íà âû÷èñëåíèå ìèíèìóìà ïðèâåäåíà òàáë. 1.6.
1.3. Îñíîâíûå ïîñòóëàòû àëãåáðû ëîãèêè
Ïðåæäå âñåãî íåîáõîäèìî óÿñíèòü ïîðÿäîê âûïîëíåíèÿ ëîãè÷åñêèõ îïåðàöèé. Åñëè íåò ñêîáîê, ñíà÷àëà ïðîèçâîäèòñÿ èíâåðòèðîâàíèå îòäåëüíûõ ïåðåìåííûõ, ïîòîì êîíúþíêöèÿ è çàòåì
20
Ò à á ë è ö à 1.7
Îñíîâíûå ïîñòóëàòû
Íàçâàíèå ïîñòóëàòà
Ïåðåìåñòèòåëüíûé (êîììóòàòèâíû é)
Ôîðìóëû
x 1 ⋅ x0 = x0 ⋅ x1 ;
x 1 ∨ x 0 = x1 ∨ x 0
Ñî÷åòàòåëüíûé (àññîöèàòèâíûé)
x2 ⋅ (x1 ⋅ x0) = (x2 ⋅ x1) ⋅ x0;
x2 ∨ (x1 ∨ x0) = (x2 ∨ x1) ∨ x0
Ðàñïðåäåëèòåëüíûé (äèñòðèáóòèâíû é)
x2 ⋅ (x1 ∨ x0) = x2 ⋅ x1 ∨ x2 ⋅ x0
äèçúþíêöèÿ. Èíâåðñèÿ ôóíêöèé, ñîñòîÿùèõ èç íàáîðà àðãóìåíòîâ, ñâÿçàííûõ ìåæäó ñîáîé äðóãèìè îïåðàöèÿìè, îñóùåñòâëÿåòñÿ
â ïîñëåäíþþ î÷åðåäü.
Ïðè íàëè÷èè ñêîáîê ñíà÷àëà âûïîëíÿþò îïåðàöèè âíóòðè íèõ,
ò. å. çäåñü íàáëþäàåòñÿ ïîëíàÿ àíàëîãèÿ ñ ïîðÿäêîì âûïîëíåíèÿ
îïåðàöèé â îáû÷íîé àëãåáðå, òîëüêî âîçâåäåíèå â ñòåïåíü çàìåíÿåòñÿ èíâåðñèåé, óìíîæåíèå êîíúþíêöèåé, à ñëîæåíèå äèçúþíêöèåé. Îñòàëüíûå ïîñòóëàòû íè÷åì íå îòëè÷àþòñÿ îò îáû÷íîé àëãåáðû (òàáë. 1.7).
1.4. Îáðàòíûå ëîãè÷åñêèå îïåðàöèè
Ëîãè÷åñêèå îïåðàöèè, ðàññìîòðåííûå â ïîäðàçä. 1.2, ïîçâîëÿþò ñëåäîâàòü îò àðãóìåíòîâ ê ôóíêöèè, ò. å. îò ïðè÷èí ê ñëåäñòâèþ. Îäíàêî àíàëîãè÷íî òîìó, êàê áûâàåò â ñëåäñòâåííûõ îðãàíàõ, ãäå èñõîäÿ èç ñîáûòèÿ èùóò ïðè÷èíû, òàê è ïðè ïðîåêòèðîâàíèè è ýêñïëóàòàöèè öèôðîâûõ óñòðîéñòâ è ñèñòåì, ÷àñòî
òðåáóåòñÿ ïî çàäàííûì âûõîäíûì ñèãíàëàì ïðè èçâåñòíîì âûõîäíîì óñòðîéñòâå îïðåäåëèòü ñèãíàëû, êîòîðûå íåîáõîäèìî
ïîäàòü íà åãî âõîäû, ÷òîáû ñïðîåêòèðîâàòü óñòðîéñòâî, ñîãëàñóþùåå îñíîâíûå âõîäû ñèñòåìû ñ âõîäàìè âûõîäíîãî óñòðîéñòâà.
Ýòî ìîæíî ñäåëàòü, èñïîëüçóÿ ëîãè÷åñêèå îïåðàöèè, îáðàòíûå
ðàññìîòðåííûì ðàíåå. Ïîäîáíî òîìó, êàê â îáû÷íîé àëãåáðå âû÷èòàíèå ÿâëÿåòñÿ îïåðàöèåé, îáðàòíîé ñëîæåíèþ, à äåëåíèå
óìíîæåíèþ, òàê è â àëãåáðå ëîãèêè îïåðàöèåé, îáðàòíîé äèçúþíêöèè, ÿâëÿåòñÿ ëîãè÷åñêîå âû÷èòàíèå (óñëîâíîå îáîçíà÷åíèå \),
à îïåðàöèåé, îáðàòíîé êîíúþíêöèè, ëîãè÷åñêîå äåëåíèå (óñëîâíîå îáîçíà÷åíèå /). ×òî êàñàåòñÿ èíâåðñèè, òî çäåñü íåò íåîáõîäèìîñòè ïðèäóìûâàòü íîâóþ îáðàòíóþ îïåðàöèþ, ïîñêîëüêó,
âûðàæàÿñü ðàäèîòåõíè÷åñêèì ÿçûêîì, îíà ÿâëÿåòñÿ âçàèìíî-îáðàòèìîé.
Äëÿ òîãî ÷òîáû óñòàíîâèòü â îòíîøåíèè îáðàòíûõ îïåðàöèé
ñîîòâåòñòâóþùèå çàêîíîìåðíîñòè, ñîñòàâèì äëÿ íèõ òàáëèöó èñòèííîñòè (òàáë. 1.8), èñïîëüçóÿ òàáë. 1.3.
21
Ò à á ë è ö à 1.8
Òàáëèöà èñòèííîñòè äëÿ îáðàòíûõ ëîãè÷åñêèõ îïåðàöèé
y
x0
x 1 = y \ x0
x1 = y / x0
0
0
0
Íåîïðåäåëåííîñòü
0
1
Çàïðåò
0
1
0
1
Çàïðåò
1
1
Íåîïðåäåëåííîñòü
1
Êàê âèäíî èç ïåðâîé ñòðîêè òàáë. 1.8, ðåçóëüòàò îïåðàöèè ëîãè÷åñêîãî äåëåíèÿ ïîëó÷èëñÿ íåîïðåäåëåííûì, ÷òî àíàëîãè÷íî
ðåçóëüòàòó îáû÷íîãî äåëåíèÿ íóëÿ íà íóëü.
Âòîðàÿ ñòðîêà ëîãè÷åñêîãî âû÷èòàíèÿ íèêàê íå ñâÿçàíà ñ
òàáë. 1.3, òàê êàê åå èñõîäíûå äàííûå ïðîòèâîðå÷àò çàêîíó äèçúþíêöèè. Òàêîé ðåçóëüòàò â àëãåáðå ëîãèêè íàçûâàåòñÿ çàïðåùåííûì.
 òðåòüåé ñòðîêå òàáë. 1.8 ðåçóëüòàò ëîãè÷åñêîãî äåëåíèÿ ÿâëÿåòñÿ çàïðåùåííûì àíàëîãè÷íî òîìó, êàê ðåçóëüòàò îáû÷íîãî äåëåíèÿ ÷èñëà, îòëè÷íîãî îò íóëÿ, íà íóëü ñòðåìèòñÿ ê áåñêîíå÷íîñòè.
È íàêîíåö, â ÷åòâåðòîé ñòðîêå òàáëèöû â ðåçóëüòàòå ëîãè÷åñêîãî âû÷èòàíèÿ ïîëó÷àåòñÿ íåîïðåäåëåííîñòü, âïîëíå îáúÿñíèìàÿ ïðèðîäîé äèçúþíêöèè: 1 ∨ x = 1.
 îòìå÷åííûõ çäåñü íåîïðåäåëåííûõ è çàïðåùåííûõ ñëó÷àÿõ
ìîæíî èñïîëüçîâàòü äëÿ îáîçíà÷åíèÿ ñèìâîë ½.
Äðóãèå ïîëó÷åííûå çíà÷åíèÿ àðãóìåíòà x1 âïîëíå îáúÿñíèìû
çàêîíàìè äèçúþíêöèè è êîíúþíêöèè.
 çàêëþ÷åíèå ïðèâåäåì ïîêà áåç âûâîäà (ñì. ïîäðàçä. 2.2) ôîðìóëû, ïîçâîëÿþùèå îñóùåñòâëÿòü îïåðàöèè ëîãè÷åñêîãî âû÷èòàíèÿ è ëîãè÷åñêîãî äåëåíèÿ:
x 0 ∨ ½ ⋅ x 0;
x1 = y \ x0 = y ⋅
x 0.
x1 = y / x0 = y ⋅ x0 ∨ ½ ⋅
Ñ ó÷åòîì íåîïðåäåëåííîñòåé ýòè ôîðìóëû ìîæíî ñóùåñòâåííî
óïðîñòèòü: x1 = y \ x0 = y / x0 = y. Óêàçàííûå ñîîòíîøåíèÿ ïîçâîëÿþò
ñôîðìóëèðîâàòü ñëåäóþùóþ òåîðåìó.
Äëÿ ïîëó÷åíèÿ òðåáóåìîãî çíà÷åíèÿ ðåçóëüòàòà äèçúþíêöèè èëè
êîíúþíêöèè ïðè îäíîì èçâåñòíîì îïåðàíäå, çíà÷åíèå êîòîðîãî íå ïðîòèâîðå÷èò çíà÷åíèþ çàäàííîé ôóíêöèè, äðóãîé îïåðàíä äîëæåí ðàâíÿòüñÿ çíà÷åíèþ ýòîé ôóíêöèè.
Âûâåäåííûå ôîðìóëû áóäóò ñïðàâåäëèâû, åñëè â íèõ x1 è x0
ïîìåíÿòü ìåñòàìè.
22
Êîíòðîëüíûå âîïðîñû
1. Êàêàÿ îïåðàöèÿ ñâÿçûâàåò èñòèííîå è ëîæíîå âûñêàçûâàíèÿ? Êàêèìè çíàêàìè îíè îáîçíà÷àþòñÿ?
2. Ñîñòàâüòå òàáëèöû èñòèííîñòè äëÿ òðåõ îñíîâíûõ ëîãè÷åñêèõ îïåðàöèé.
3.  êàêîé ïîñëåäîâàòåëüíîñòè äîëæíû ïðîèçâîäèòüñÿ ëîãè÷åñêèå îïåðàöèè?
4. ×åì îòëè÷àåòñÿ äèçúþíêöèÿ îò îáû÷íîãî ñóììèðîâàíèÿ?
5. Ïîÿñíèòå ëîãè÷åñêèå îïåðàöèè íà äèàãðàììàõ Ýéëåðà.
6. ×òî ïðåäñòàâëÿåò ñîáîé çàêîí äâîéíîãî îòðèöàíèÿ?
7. Íà êîìïüþòåðå â ñèñòåìå Word îïðåäåëèòå çíà÷åíèÿ NOT(FALSE),
NOT(0), NOT(TRUE), NOT(1), OR(0;0), OR(0;1), OR(1;1), AND(0;0),
AND(0;1), AND(1;1). Óáåäèòåñü â ýêâèâàëåíòíîñòè îïåðàöèé OR è MAX,
AND è MIN ñ âêëþ÷åíèåì ñèìâîëà íåîïðåäåëåííîñòè ½.
8. Êàê äîêàçàòü çàêîí ëîæíîãî ïîëîæåíèÿ?
9. Îáúÿñíèòå çàêîí òàâòîëîãèè.
10. Ñôîðìóëèðóéòå çàêîíû äîïîëíèòåëüíîñòè.
11.  ÷åì çàêëþ÷àåòñÿ ñìûñë îáðàòíûõ ëîãè÷åñêèõ îïåðàöèé?
12. ×òî òàêîå ïåðåìåñòèòåëüíûå çàêîíû?
13. Îáúÿñíèòå ñî÷åòàòåëüíûå çàêîíû.
14.  ÷åì çàêëþ÷àåòñÿ ðàñïðåäåëèòåëüíûé çàêîí?
ÃËÀÂÀ 2
ÀÍÀËÈÒÈ×ÅÑÊÈÅ ÔÎÐÌÛ ÏÐÅÄÑÒÀÂËÅÍÈß
ËÎÃÈ×ÅÑÊÈÕ ÔÓÍÊÖÈÉ
2.1. Ñîâåðøåííàÿ äèçúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà
ÑÄÍÔ, íàçûâàåìàÿ åùå êàíîíè÷åñêîé, ïîçâîëÿåò ëåãêî ïðîèçâîäèòü ñ÷èòûâàíèå â àíàëèòè÷åñêîì âèäå ôóíêöèè, ïðåäñòàâëåííîé â òàáëè÷íîé ôîðìå. Ïðàâèëî, ïî êîòîðîìó âûïîëíÿåòñÿ ýòî
ïðåäñòàâëåíèå, îñíîâàíî íà òåîðåìå Øåííîíà, êîòîðàÿ ôîðìóëèðóåòñÿ ñëåäóþùèì îáðàçîì: ëþáóþ ñêîëü óãîäíî ñëîæíóþ ëîãè÷åñêóþ ôóíêöèþ m àðãóìåíòîâ ìîæíî ïðåäñòàâèòü äèçúþíêöèåé äâóõ
êîíúþíêöèé, ò. å.
y (xm−1, xm−2, ¾ , xi, ¾ , x1, x0) =
xi ∨
= y (xm−1, xm−2, ¾ , 0, ¾ , x1, x0) ⋅
∨ y (xm−1, xm−2, ¾ , 1, ¾ , x1, x0) ⋅ xi.
(2.1)
Ñïðàâåäëèâîñòü ýòîé òåîðåìû óñòàíàâëèâàåòñÿ ïîñëåäîâàòåëüíîé ïîäñòàíîâêîé âîçìîæíûõ çíà÷åíèé ïåðåìåííîé xi.
23
Ò à á ë è ö à 2.1
Òàáëèöà èñòèííîñòè ôóíêöèè O(: )
Íîìåð
âàðèàíòà
xi
z1
z0
y (X )
Ïðèìå÷àíèÿ
0
0
0
0
0
Äîëæíî áûòü y (xi = 0)
1
0
0
1
y (xi = 1)
Äîëæíî áûòü y (xi = 0)
2
0
1
0
y (xi = 0)
z 1 = xi
3
0
1
1
y (xi = 0) ∨ y (xi = 1)
Äîëæíî áûòü y (xi = 0)
4
1
0
0
0
Äîëæíî áûòü y (xi = 1)
5
1
0
1
y (xi = 1)
z0 = xi
6
1
1
0
y (xi = 0)
Äîëæíî áûòü y (xi = 1)
7
1
1
1
y (xi = 0) ∨ y (xi = 1)
Äîëæíî áûòü y (xi = 1)
Îòìåòèì, ÷òî âûðàæåíèå (2.1) íàïîìèíàåò ôîðìóëó, âûâåäåííóþ äëÿ ïðåäñòàâëåíèÿ îáðàòíûõ ôóíêöèé, ãäå â îäíî ñëàãàåìîå
âõîäèò îïðåäåëåííàÿ ïåðåìåííàÿ x0 â ïðÿìîé ôîðìå, à â äðóãîå
â èíâåðñíîé.
Äîêàçàòåëüñòâî òåîðåìû íà÷íåì ñ òîãî, ÷òî ïðåäñòàâèì èñõîäíóþ ôóíêöèþ â âèäå äèçúþíêöèè äâóõ êîíúþíêöèé, â êàæäîé èç êîòîðûõ ñîìíîæèòåëÿìè âîçüìåì íåîïðåäåëåííûå ôóíêöèè z1 è z0:
y (xm−1, ¾ , xi, ¾, x0) =
= y (xm−1, ¾, 0, ¾, x0) ⋅ z1 ∨ y (xm−1, ¾ , 1, ¾ , x0) ⋅ z0.
Ñîñòàâèì òàáëèöó, ñîîòâåòñòâóþùóþ óêàçàííîìó ñîîòíîøåíèþ
(òàáë. 2.1).
Àíàëèç âñåõ âîñüìè âîçìîæíûõ âàðèàíòîâ èç òàáë. 2.1 ïîêàçûâàåò, ÷òî òîëüêî äâà èç íèõ (âòîðîé è ïÿòûé) ïîäõîäÿò äëÿ òðåáóåìîãî ïðåäñòàâëåíèÿ ôóíêöèè. Âî âòîðîì âàðèàíòå çíà÷åíèÿ àðãóìåíòîâ xi è z1 íå ñîâïàäàþò, ïîýòîìó îäèí èç íèõ äîëæåí áûòü
ïðîèíâåðòèðîâàí.  ïÿòîì âàðèàíòå çíà÷åíèÿ xi è z0 ñîâïàäàþò, ò. å.
îíè ðàâíû.
Ïðè÷èíû íåãîäíîñòè îñòàëüíûõ øåñòè âàðèàíòîâ ïðèâåäåíû â
ïðèìå÷àíèÿõ òàáëèöû. Òàêèì îáðàçîì, òåîðåìà ìîæåò ñ÷èòàòüñÿ
äîêàçàííîé.
Òåïåðü íå ñîñòàâèò òðóäà äîêàçàòü òåîðåìó î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé â ñîâåðøåííîé äèçúþíêòèâíîé íîðìàëüíîé ôîðìå.
Âñÿêàÿ ñêîëü óãîäíî ñëîæíàÿ ëîãè÷åñêàÿ ôóíêöèÿ y îò m ïåðåìåííûõ ìîæåò áûòü ïðåäñòàâëåíà â ÑÄÍÔ, ò. å. äèçúþíêöèåé ïðî24
èçâåäåíèé çíà÷åíèé ýòîé ôóíêöèè yX íà ìèíòåðìû MnX, ñîîòâåòñòâóþùèå íàáîðàì àðãóìåíòîâ X:
X max
y = ∨ y X ⋅ Mn X ,
X =0
ãäå X ïîðÿäêîâûé íîìåð íàáîðà àðãóìåíòîâ (âåêòîð àðãóìåíòîâ); Xmax = 2m − 1 ìàêñèìàëüíîå çíà÷åíèå íîìåðà íàáîðà àðãóìåíòîâ; MnX ìèíòåðì, ÿâëÿþùèéñÿ êîíúþíêöèåé âñåõ àðãóìåíòîâ, ôîðìà ïðåäñòàâëåíèÿ êîòîðûõ (ïðÿìàÿ èëè èíâåðñíàÿ)
çàâèñèò îò òîãî, ÷åìó ðàâåí äàííûé àðãóìåíò xi â äàííîì íàáîðå
X: åñëè îí ðàâåí íóëþ â èíâåðñíîé, åñëè åäèíèöå â ïðÿìîé.
Ïðèìåíèì òåîðåìó Øåííîíà, ïîäñòàâèâ â ôîðìóëó (2.1) âìåñòî xi ñàìûé ìëàäøèé àðãóìåíò x0, çàòåì ðàñêðîåì ôóíêöèþ ïî
ñëåäóþùåìó àðãóìåíòó x1 è òàê äàëåå äî ñàìîãî ïîñëåäíåãî çíà÷åíèÿ xm-1 âêëþ÷èòåëüíî:
y (xm−1, ¾ , x1, x0) = y (xm−1, ¾ , x1, 0) ⋅
x 0 ∨ y (xm−1, ¾ , x1, 1) ⋅ x0 =
x 1 ⋅
x 0 ∨ y (xm−1, ¾ , 0, 1) ⋅
x 1 ⋅ x0 ∨
= y (xm−1, ¾ , 0, 0) ⋅
∨ y (xm−1, ¾ , 1, 0) ⋅ x1 ⋅
x 0 ∨ y (xm−1, ¾ , 1, 1) ⋅ x1 ⋅ x0 =
..................
= y (0, ¾ , 0, 0) ⋅
x
m − 1 ⋅ ... ⋅ x 1 ⋅ x 0 ∨ ¾ ∨ y (1, ¾ , 1, 1) ⋅ xm−1 ⋅ ¾ ⋅ x1 ⋅ x0 =
X max
= ∨ y X ⋅ Mn X ,
X =0
÷òî è òðåáîâàëîñü äîêàçàòü.
Ëåãêî çàìåòèòü, ÷òî ÑÄÍÔ àíàëîãè÷íà èçâåñòíûì ðàçëîæåíèÿì ôóíêöèé â ðÿäû Ôóðüå, Óîëøà è äð. Ïîýòîìó ðàññìîòðåííóþ
òåîðåìó ìîæíî íàçâàòü òåîðåìîé î ðàçëîæåíèè ëîãè÷åñêèõ ôóíêöèé
â ðÿä ïî ìèíòåðìàì.
Òåïåðü ïîñìîòðèì, êàêèìè ñâîéñòâàìè îáëàäàþò ìèíòåðìû. Äëÿ
ýòîãî ñîñòàâèì èõ òàáëèöó èñòèííîñòè (òàáë. 2.2).
Ò à á ë è ö à 2.2
Òàáëèöà èñòèííîñòè ìèíòåðìîâ
Àðãóìåíòû
Ìèíòåðìû
:
N1
N0
Mn0
Mn1
Mn2
Mn3
0
0
0
1
0
0
0
1
0
1
0
1
0
0
2
1
0
0
0
1
0
3
1
1
0
0
0
1
25
Ò à á ë è ö à 2.3
Òàáëèöà èñòèííîñòè ïðåîáðàçîâàòåëÿ êîäà «1 èç 4»
â íàòóðàëüíûé äâîè÷íûé êîä
Àðãóìåíòû
Ôóíêöèè
:
N3
N2
N1
N0
O1
O0
1
0
0
0
1
0
0
2
0
0
1
0
0
1
4
0
1
0
0
1
0
8
1
0
0
0
1
1
Îáðàòèì âíèìàíèå íà òî, ÷òî àðãóìåíòû x1 è x0 ïðåäñòàâëÿþò
ñîáîé äâîè÷íûå ðàçðÿäû ÷èñëà X. Êðîìå òîãî, êàæäûé ìèíòåðì
ñòàíîâèòñÿ ðàâíûì åäèíèöå òîëüêî â îäíîì èç íàáîðîâ, à èìåííî
â òîì, êîòîðîìó ñîîòâåòñòâóåò åãî íîìåð. Ïîñëåäíåå îáñòîÿòåëüñòâî, âî-ïåðâûõ, ðîäíèò äîêàçàííóþ òåîðåìó ñ òåîðåìîé îòñ÷åòîâ, èçâåñòíóþ ó íàñ ïîä íàçâàíèåì òåîðåìû Êîòåëüíèêîâà. Âîâòîðûõ, ïîçâîëÿåò îòíåñòè ìèíòåðìû ê êîäàì «îäèí èç m» è,
ñëåäîâàòåëüíî, ñ÷èòàòü òàáë. 2.2 òàáëèöåé èñòèííîñòè ïðåîáðàçîâàòåëÿ íàòóðàëüíîãî äâîè÷íîãî êîäà â êîä «1 èç m» (â äàííîì
êîíêðåòíîì ñëó÷àå â êîä «1 èç 4»).
 êà÷åñòâå ïðèìåðà ïðèìåíåíèÿ ðàññìîòðåííîé òåîðåìû ïîëó÷èì àíàëèòè÷åñêèå âûðàæåíèÿ â ÑÄÍÔ ïðåîáðàçîâàòåëÿ êîäà
«1 èç 4» â íàòóðàëüíûé äâîè÷íûé êîä. Ñîñòàâèì äëÿ íà÷àëà òàáëèöó èñòèííîñòè òàêîãî êîäîïðåîáðàçîâàòåëÿ (òàáë. 2.3).
Ñëåäóåò çàìåòèòü, ÷òî òàáë. 2.3 ÿâëÿåòñÿ ñîêðàùåííîé, òàê êàê
â íåé îòñóòñòâóþò çàïðåùåííûå êîìáèíàöèè àðãóìåíòîâ, ïîýòîìó ïðèâåäåì äëÿ íàãëÿäíîñòè ñîîòâåòñòâóþùóþ ïîëíóþ òàáëèöó
(òàáë. 2.4).
Èç òàáë. 2.4 âèäíî, ÷òî çàïðåùåííûìè ÿâëÿþòñÿ òå íàáîðû àðãóìåíòîâ, êîòîðûå íå ñîîòâåòñòâóþò êîäó «1 èç 4». Ðàçðåøåííûå
íàáîðû àðãóìåíòîâ çäåñü âûäåëåíû ñåðûì ôîíîì.
 ñîîòâåòñòâèè ñ ðàññìîòðåííîé òåîðåìîé çàïèøåì â ÑÄÍÔ
âûðàæåíèÿ äëÿ äâóõ èñêîìûõ ôóíêöèé, îïóñêàÿ ìèíòåðìû, ñîîòâåòñòâóþùèå íóëåâûì çíà÷åíèÿì ýòèõ ôóíêöèé â íàáîðàõ àðãóìåíòîâ, è óìíîæàÿ èõ íà ½ ïðè çàïðåùåííûõ íàáîðàõ àðãóìåíòîâ, êàê ýòî áûëî îãîâîðåíî ðàíåå:
x 3 ·
x 2 ·
x 1 ·
x0 ∨
x 3 ·
x 2 · x1 ·
x 0 ∨ ½
x 3 ·
x 2 · x1 · x 0 ∨ ½
x 3 · x2 ·
x 1 · x0 ∨
y0 = ½
x 0 ∨ ½
x 3 · x 2 · x1 · x 0 ∨ x 3 ·
x 2 ·
x 1 ·
x 0 ∨ ½ x3 ·
x 2 ·
x 1 · x0 ∨
∨ ½
x 3 · x 2 · x1 ·
∨ ½ x3 ·
x 2 · x1 ·
x 0 ∨ ½ x3 ·
x 2 · x1 · x 0 ∨ ½ x 3 · x2 ·
x 1 ·
x 0 ∨ ½ x3 · x 2 ·
x 1 · x0 ∨
26
Ò à á ë è ö à 2.4
Ïîëíàÿ òàáëèöà èñòèííîñòè ïðåîáðàçîâàòåëÿ êîäà «1 èç 4»
â íàòóðàëüíûé äâîè÷íûé êîä
Àðãóìåíòû
Ôóíêöèè
:
N3
N2
N1
N0
O1
O0
0
0
0
0
0
½
½
1
0
0
0
1
0
0
2
0
0
1
0
0
1
3
0
0
1
1
½
½
4
0
1
0
0
1
0
5
0
1
0
1
½
½
6
0
1
1
0
½
½
7
0
1
1
1
½
½
8
1
0
0
0
1
1
9
1
0
0
1
½
½
10
1
0
1
0
½
½
11
1
0
1
1
½
½
12
1
1
0
0
½
½
13
1
1
0
1
½
½
14
1
1
1
0
½
½
15
1
1
1
1
½
½
∨ ½ x3 · x 2 · x 1 ·
x 0 ∨ ½ x 3 · x 2 · x 1 · x 0;
x 3 ·
x 2 ·
x 1 ·
x 0 ∨ ½
x 3 ·
x 2 · x1 · x 0 ∨
x 3 · x2 ·
x 1 ·
x 0 ∨ ½
x 3 · x2 ·
x 1 · x0 ∨
y1 = ½
x 0 ∨ ½
x 3 · x2 · x 1 · x 0 ∨ x 3 ·
x 2 ·
x 1 ·
x 0 ∨ ½ x3 ·
x 2 ·
x 1 · x0 ∨
∨ ½
x 3 · x2 · x1 ·
x 2 · x1 ·
x 0 ∨ ½ x3 ·
x 2 · x 1 · x 0 ∨ ½ x3 · x 2 ·
x 1 ·
x 0 ∨ ½ x3 · x2 ·
x 1 · x0 ∨
∨ ½ x3 ·
x 0 ∨ ½ x3 · x 2 · x 1 · x0 .
∨ ½ x 3 · x 2 · x1 ·
Íåðåäêî ïðèìåíÿþò óñëîâíûå âûðàæåíèÿ ôóíêöèé â ÑÄÍÔ.
Íàïðèìåð, äëÿ ðàññìîòðåííîãî ñëó÷àÿ ìîæíî çàïèñàòü
y0 = ∨ (2, 8, ½ (0, 3, 5 ... 7, 9 ... 15));
y1 = ∨ (4, 8, ½ (0, 3, 5 ... 7, 9 ... 15)).
27
 êà÷åñòâå äðóãîãî ïðèìåðà ïðèìåíåíèÿ ðàññìîòðåííîé òåîðåìû ïîëó÷èì â ÑÄÍÔ ôóíêöèþ, îïðåäåëåííóþ äèçúþíêöèåé. Èç
òàáë. 1.3 èìååì
y =
x 1 · x0 ∨ x 1 ·
x 0 ∨ x 1 · x 0.
Èñïîëüçóÿ ñâîéñòâà äèçúþíêöèè, ìîæíî ïåðåéòè îò ÑÄÍÔ ê
áîëåå êîðîòêèì àíàëèòè÷åñêèì âûðàæåíèÿì.
 ðàçâèòèå çàêîíà ëîæíîãî ïîëîæåíèÿ è â êà÷åñòâå ñëåäñòâèÿ
òåîðåìû î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé â ÑÄÍÔ ìîæíî
çàêëþ÷èòü, ÷òî èíâåðñèÿ îòñ÷åòîâ ëîãè÷åñêîé ôóíêöèè ïðèâîäèò
ê èíâåðñèè ñàìîé ôóíêöèè:
X max
y ( X ) = ∨ y X ⋅ Mn X .
X =0
Ýòî ñâîéñòâî áóäåì èñïîëüçîâàòü â äàëüíåéøåì.
Ñëåäóåò îòìåòèòü, ÷òî äëÿ ïðåäñòàâëåíèÿ ëîãè÷åñêèõ ôóíêöèé
ïîìèìî ÑÄÍÔ ïðèìåíÿåòñÿ (õîòÿ è íå ÷àñòî) è ñîâåðøåííàÿ êîíúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà (ñì. ïîäðàçä. 2.3).
2.2. Ñîêðàùåííûå, òóïèêîâûå è ìèíèìàëüíûå
äèçúþíêòèâíûå íîðìàëüíûå ôîðìû ïðåäñòàâëåíèÿ ôóíêöèé
Ëîãè÷åñêèå ôóíêöèè, ïðåäñòàâëåííûå â ÑÄÍÔ, óäîáíû ïðè
èõ ñ÷èòûâàíèè ñ òàáëèö èñòèííîñòè, îäíàêî â îáùåì îíè ãðîìîçäêè è äëÿ èõ ñîêðàùåíèÿ èñïîëüçóþò ìåòîäû ìèíèìèçàöèè.
Ïðè÷åì ìèíèìèçàöèþ ïðîâîäÿò â òðè ýòàïà, ïîëó÷àÿ íà ïåðâîì ýòàïå ñîêðàùåííûå ôóíêöèè, íà âòîðîì òóïèêîâûå è íà
òðåòüåì ìèíèìàëüíûå. Ðàññìîòðèì ïîñëåäîâàòåëüíî ýòè ýòàïû.
Íà ïåðâîì ýòàïå ïðîèçâîäèòñÿ ñêëåèâàíèå ñîñåäíèõ ìèíòåðìîâ è èìïëèêàíò, íà âòîðîì èñêëþ÷åíèå èçáûòî÷íûõ1 èìïëèêàíò, íà òðåòüåì âûáîð íàèìåíüøåãî âàðèàíòà òóïèêîâîé ôóíêöèè, ïîëó÷åííîãî â ðåçóëüòàòå âòîðîãî ýòàïà.
Ñîïðÿæåííûìè2 (ñîñåäíèìè, èëè ñìåæíûìè)3 ÿâëÿþòñÿ ìèíòåðìû, îòëè÷àþùèåñÿ òîëüêî îäíîé ïåðåìåííîé (ò. å. â îäèí ìèíòåðì ïåðåìåííàÿ xi âõîäèò â ïðÿìîé ôîðìå, à â äðóãîé â èíâåðñíîé). Íàïðèìåð, åñëè ìèíòåðì âåêòîðà àðãóìåíòîâ X
1
Èçáûòî÷íûìè îíè íàçûâàþòñÿ ïîòîìó, ÷òî â ñîâîêóïíîñòè ñ äðóãèìè ìèíòåðìàìè è èìïëèêàíòàìè íå îêàçûâàþò íèêàêîãî âëèÿíèÿ íà çíà÷åíèÿ ôóíêöèè
ïðè ëþáûõ çíà÷åíèÿõ åå àðãóìåíòîâ.
2
Ñîïðÿæåííûìè îíè íàçûâàþòñÿ ïî àíàëîãèè ñ êîìïëåêñíûìè ïåðåìåííûìè, ñóììà êîòîðûõ ïðè ðàâåíñòâå èõ ìíèìûõ ñîñòàâëÿþùèõ ïî àáñîëþòíîìó
çíà÷åíèþ è ðàçëè÷èè òîëüêî â çíàêàõ ëèøåíà ìíèìîé ñîñòàâëÿþùåé.
3
Ñîñåäíèìè, èëè ñìåæíûìè, îíè íàçûâàþòñÿ ïîòîìó, ÷òî ïðè âíåñåíèè â
òàáëèöó èñòèííîñòè êîäà Ãðåÿ, èõ ñòðîêè îêàçûâàþòñÿ ñîñåäíèìè.
28
MnX = xm−1 · xm−2 · ... · xi+1 · xi · xi−1· ... · x1 · x0,
òî ñîïðÿæåííûì åìó ïî ïåðåìåííîé xi áóäåò ìèíòåðì
MnX*(i ) = xm−1 · xm−2 · ... · xi+1 ·
x i · xi−1 · ... · x1 · x0.
Äèçúþíêöèÿ äâóõ ñîïðÿæåííûõ ìèíòåðìîâ (ñêëåèâàíèå) ïðèâîäèò ê îáðàçîâàíèþ èìïëèêàíòû ïåðâîãî óðîâíÿ ïðîñòîé êîíúþíêöèè, ñîäåðæàùåé (m − 1) ïåðåìåííóþ:
MnX ∨ MnX*(i ) = xm−1 · xm−2 · ... · xi+1 · (xi ∨
x i) · xi−1 · ... · x1 · x0 =
= xm−1 · xm−2 · ... · xi+1 · xi−1 · ... · x1 · x0 = ImpX (i ).
Àíàëîãè÷íî îñóùåñòâëÿåòñÿ äàëüíåéøàÿ ìèíèìèçàöèÿ ëîãè÷åñêîé ôóíêöèè ïóòåì ïîèñêà è ñêëåèâàíèÿ ñîïðÿæåííûõ èìïëèêàíò ïåðâîãî, âòîðîãî, òðåòüåãî óðîâíåé è ò. ä.
 ðåçóëüòàòå ïåðâîãî ýòàïà ìèíèìèçàöèè ìîãóò îáðàçîâàòüñÿ
èçáûòî÷íûå èìïëèêàíòû, êîòîðûå íåîáõîäèìî èñêëþ÷èòü èç ñîñòàâà ëîãè÷åñêîé ôóíêöèè, ÷òî è âûïîëíÿåòñÿ íà âòîðîì ýòàïå.
Ïîÿñíèì ýòó ìåòîäèêó íà ïðèìåðå îáðàòíûõ ëîãè÷åñêèõ ôóíêöèé: âû÷èòàíèÿ è äåëåíèÿ. Íà îñíîâå òàáë. 1.8 ñîñòàâèì òàáëèöó
èìïëèêàíò (òàáë. 2.5).
 òàáë. 2.5 äëÿ íàãëÿäíîñòè ïðèâåäåíû ïàðû èìïëèêàíò, êîòîðûå ïî çàêîíó èäåìïîòåíòíîñòè ïðåâðàùàþòñÿ â îäèíî÷íûå. Èìïëèêàíòû ñ ñèìâîëîì íåîïðåäåëåííîñòè ½ â îêîí÷àòåëüíîå âûðàæåíèå äëÿ êðàòêîñòè íå âíîñÿòñÿ. Îñòàþòñÿ ëèøü èìïëèêàíòû,
ïðåäñòàâëåííûå çíà÷åíèåì ñàìîé ôóíêöèè y. Òàêèì îáðàçîì, ïðèõîäèì ê òðèâèàëüíîìó âûðàæåíèþ x1 = y \ x0 = y / x0 = y.
Ðàññìîòðèì åùå îäèí ïðèìåð îïðåäåëåíèÿ ìèíèìèçèðîâàííûõ ôóíêöèé ïðåîáðàçîâàòåëÿ íàòóðàëüíîãî äâîè÷íîãî êîäà â êîä
Ãðåÿ (òàáë. 2.6).
Êàê âèäíî èç òàáë. 2.6, êîä Ãðåÿ öèêëè÷åñêèé, ò. å. ìîæåò íåïðåðûâíî ïîâòîðÿòüñÿ. Êðîìå òîãî, â ñîñåäíèõ ñòðîêàõ òàáëèöû
êîäîâûå íàáîðû ðàçëè÷àþòñÿ ìåæäó ñîáîé òîëüêî â îäíîì èç ðàçÒ à á ë è ö à 2.5
Òàáëèöà èìïëèêàíò ôóíêöèé ëîãè÷åñêîãî âû÷èòàíèÿ è äåëåíèÿ
Íîìåð
Ìèíòåðì
ìèíòåðìà
Ëîãè÷åñêîå âû÷èòàíèå
Ëîãè÷åñêîå äåëåíèå
O5
Imp1(O)
Imp2(N0)
O5
Imp0(O)
Imp2(N0)
0
O · N0
0
½
½ N0
1
O · N0
½
½ N0
0
2
O · N0
1
O
½
½ N0
O
3
O · N0
½
½ N0
O
1
O
29
Ò à á ë è ö à 2.6
Òàáëèöà èñòèííîñòè êîäà Ãðåÿ
X
x
x
x
y
y
y
!
"
#
$
%
ðÿäîâ, âñëåäñòâèå ÷åãî åãî íàçûâàþò ýâîëþöèîííûì. Áëàãîäàðÿ ýòèì
ñâîéñòâàì êîä Ãðåÿ øèðîêî ïðèìåíÿåòñÿ â àíàëîãî-öèôðîâûõ
ïðåîáðàçîâàòåëÿõ è êîäîâûõ äèàãðàììàõ (ñì. ãë. 4).
 äàííîì ïðèìåðå ïðåäñòàâëåí òðåõðàçðÿäíûé êîä, ñëåäîâàòåëüíî, è ôóíêöèé òîæå òðè. Ñîñòàâèì ñîîòâåòñòâóþùóþ òàáëèöó
ìèíòåðìîâ è èìïëèêàíò (òàáë. 2.7).
Óáðàâ ïîâòîðíûå èìïëèêàíòû, ïîëó÷èì
1 ∨ x1) ∨ x2(x
0 ∨ x0 ) = x2 ;
y2 = x2
x 1 ∨ x2 x1 ∨ x2
x 0 ∨ x2 x0 = x2(x
x 2 x1 ∨ x2
x 1 = x2 ⊕ x1; y0 =
x 1 x0 ∨ x1
x 0 = x 1 ⊕ x 0.
y1 =
Ò à á ë è ö à 2.7
Òàáëèöà ìèíòåðìîâ è èìïëèêàíò êîäà Ãðåÿ
30
:
Mn:
O2
Imp(0)
Imp(1)
O1
Imp(0)
O0
Imp(2)
0
N2 N1 N0
0
0
0
1
N2 N1 N0
0
0
1
N1 N0
2
N2 N1 N0
0
1
N2 N1
1
N1 N0
3
N2 N1 N0
0
1
N2 N1
0
4
N2 N1 N0
1
N2 N1
N2 N0
1
N2 N1
0
5
N2 N1 N0
1
N2 N1
N2 N0
1
N2 N1
1
N1 N0
6
N2 N1 N0
1
N2 N1
N2 N0
0
1
N1 N0
7
N2 N1 N0
1
N2 N1
N2 N0
0
0
Ïîñëåäíèå äâå ôóíêöèè èìåþò ñïåöèàëüíûå íàçâàíèÿ íåðàâíîçíà÷íîñòè, èëè ñóììèðîâàíèÿ ïî ìîäóëþ äâà, è ñîêðàùåííîå
îáîçíà÷åíèå êðåñòèê âíóòðè êðóæêà.
Âûâåäåííûå âûðàæåíèÿ ìîæíî îáîáùèòü íà áîëåå ìíîãîðàçðÿäíûé êîäîïðåîáðàçîâàòåëü: yi = xi+1 ⊕ xi;
 êà÷åñòâå åùå îäíîãî ïðèìåðà ðàññìîòðèì ìèíèìèçàöèþ ôóíêöèè îïåðàöèè äèçúþíêöèè, ïîëó÷åííîé ðàíåå â ÑÄÍÔ:
y =
x 1 · x0 ∨ x 1 ·
x 0 ∨ x 1 · x0 =
x 1 · x 0 ∨ x 1 · x0 ∨ x 1 ·
x 0 ∨ x1 · x 0 =
1 ∨ x1) ⋅ x0 ∨ x1 · (x
0 ∨ x0) = x0 ∨ x1.
= (x
Êàê è ñëåäîâàëî îæèäàòü, â ðåçóëüòàòå ìèíèìèçàöèè ïîëó÷èëè
â ÷èñòîì âèäå äèçúþíêöèþ.
Áîëåå ñëîæíûå ôóíêöèè ïðîùå ìèíèìèçèðîâàòü ñ ïîìîùüþ
ÝÂÌ (ñì. ãë. 3) èëè ñïåöèàëüíûõ ãðàôè÷åñêèõ ìåòîäîâ, îñíîâàííûõ íà ïðèìåíåíèè äèàãðàìì (ñì. ãë. 4).
2.3. Ñîâåðøåííàÿ êîíúþíêòèâíàÿ íîðìàëüíàÿ ôîðìà
ÑÊÍÔ, íàçûâàåìàÿ òàê æå, êàê è ÑÄÍÔ, åùå è êàíîíè÷åñêîé,
óäîáíà òåì, ÷òî ïîçâîëÿåò ëåãêî ïðîèçâîäèòü ñ÷èòûâàíèå â àíàëèòè÷åñêîì âèäå ôóíêöèè, ïðåäñòàâëåííîé â òàáëè÷íîé ôîðìå.
Ïðàâèëî, ïî êîòîðîìó âûïîëíÿåòñÿ ýòî ïðåäñòàâëåíèå, îñíîâàíî
íà ñëåäóþùåé òåîðåìå: ëþáóþ ñêîëü óãîäíî ñëîæíóþ ëîãè÷åñêóþ
ôóíêöèþ m àðãóìåíòîâ ìîæíî ïðåäñòàâèòü êîíúþíêöèåé äâóõ äèçúþíêöèé, ò. å.
y (xm−1, xm−2, ... , xi, ... , x1, x0) =
= [y (xm−1, xm−2, ... , 0, ... , x1, x0) ∨ xi] ½
½ [y (xm−1, xm−2, ... , 1, ... , x1, x0) ∨
x i].
(2.2)
Ñïðàâåäëèâîñòü ýòîé òåîðåìû óñòàíàâëèâàåòñÿ ïîñëåäîâàòåëüíîé ïîäñòàíîâêîé âîçìîæíûõ çíà÷åíèé ïåðåìåííîé xi, (ñì. ïîäðàçä. 2.1).
Äîêàçàòåëüñòâî òåîðåìû íà÷íåì ñ òîãî, ÷òî ïðåäñòàâèì èñõîäíóþ ôóíêöèþ â âèäå êîíúþíêöèè äâóõ äèçúþíêöèé, â êàæäîé èç êîòîðûõ ñîìíîæèòåëÿìè âîçüìåì íåîïðåäåëåííûå ôóíêöèè z1 è z0:
y (xm−1, ... , xi, ... , x0) =
= [y (xm−1, ... , 0, ... , x0) ∨ z1] ⋅ [y (xm−1, ... , 1, ... , x0) ∨ z0].
31
Ò à á ë è ö à 2.8
Òàáëèöà èñòèííîñòè ôóíêöèè O (: )
Íîìåð
âàðèàíòà
xi
z1
z0
y (X)
Ïðèìå÷àíèÿ
0
0
0
0
y (xi = 0) ⋅ y (xi = 1)
Äîëæíî áûòü y (xi = 0)
1
0
0
1
y (xi = 0)
z1 = xi
2
0
1
0
y (xi = 1)
Äîëæíî áûòü y (xi = 0)
3
0
1
1
1
Äîëæíî áûòü y (xi = 0)
4
1
0
0
y (xi = 0) ⋅ y (xi = 1)
Äîëæíî áûòü y (xi = 1)
5
1
0
1
y (xi = 1)
z0 = xi
6
1
1
0
y (xi = 0)
Äîëæíî áûòü y (xi = 1)
7
1
1
1
1
Äîëæíî áûòü y (xi = 1)
Ñîñòàâèì òàáëèöó, ñîîòâåòñòâóþùóþ ïðèâåäåííîìó âûðàæåíèþ (òàáë. 2.8).
Àíàëèç âñåõ âîñüìè âîçìîæíûõ âàðèàíòîâ èç òàáë. 2.8 ïîêàçûâàåò, ÷òî òîëüêî äâà èç íèõ (ïåðâûé è ïÿòûé) ïîäõîäÿò äëÿ òðåáóåìîãî ïðåäñòàâëåíèÿ ôóíêöèè.  ïåðâîì âàðèàíòå çíà÷åíèÿ xi è z1
ñîâïàäàþò, ÷òî è îòîáðàæåíî èõ ðàâåíñòâîì.  ïÿòîì âàðèàíòå çíà÷åíèÿ xi è z 0 íå ñîâïàäàþò, ïîýòîìó òðåáóåòñÿ èíâåðñèÿ. Ïðè÷èíû
íåãîäíîñòè îñòàëüíûõ øåñòè âàðèàíòîâ ïðèâåäåíû â ïðèìå÷àíèÿõ òàáëèöû. Òàêèì îáðàçîì, òåîðåìà ìîæåò ñ÷èòàòüñÿ äîêàçàííîé.
Òåïåðü äîêàæåì ñïðàâåäëèâîñòü åùå îäíîãî ñîîòíîøåíèÿ, êîòîðîå ïîíàäîáèòñÿ ïðè âûâîäå ôîðìóëû ñîâåðøåííîé êîíúþíêòèâíîé íîðìàëüíîé ôîðìû:
(a ∨ c) ⋅ (b ∨ c) = a ⋅ b ∨ c.
(2.3)
Èñïîëüçóåì äëÿ ëåâîé ÷àñòè âûðàæåíèÿ (2.3) ñâîéñòâî ðàñïðåäåëèòåëüíîãî çàêîíà, ò. å. ðàñêðîåì ñêîáêè:
(a ∨ c) ⋅ (b ∨ c) = a ⋅ b ∨ a ⋅ c ∨ b ⋅ c ∨ c ⋅ c.
Ó÷òåì çàêîí òàâòîëîãèè (c ⋅ c = c) è çàêîí óìíîæåíèÿ íà åäèíèöó (c = c ⋅ 1) è ñíîâà èñïîëüçóåì ðàñïðåäåëèòåëüíûé çàêîí:
a⋅b ∨ a⋅c ∨ b⋅c ∨ c⋅c = a⋅b ∨ a⋅c ∨ b⋅c ∨ c =
= a ⋅ b ∨ a ⋅ c ∨ b ⋅ c ∨ c ⋅ 1 = a ⋅ b ∨ c ⋅ (a ∨ b ∨ 1).
Ïðèìåíèâ ê ïîñëåäíåìó âûðàæåíèþ çàêîí ëîãè÷åñêîãî ñëîæåíèÿ ñ åäèíèöåé (a ∨ b ∨ 1 = 1), çàïèøåì
a ⋅ b ∨ c ⋅ (a ∨ b ∨ 1) = a ⋅ b ∨ c ⋅ 1.
32
Ñíîâà èñïîëüçîâàâ çàêîí óìíîæåíèÿ íà åäèíèöó (c ⋅ 1 = c), ïîëó÷èì èñêîìîå ñîîòíîøåíèå (2.3).
Òåïåðü ïðèñòóïèì ê âûâîäó âûðàæåíèÿ â ÑÊÍÔ. Äëÿ ýòîãî çàïèøåì ñîîòíîøåíèå (2.2) ïðè i = 0:
y (xm−1, xm−2, ... , x2, x1, x0) =
x 0].
= [y (xm−1, xm−2, ... , x2, x1, 0) ∨ x0] ⋅ [y (xm−1, xm−2, ... , x2, x1, x0) ∨
Àíàëîãè÷íî ðàñêðîåì àðãóìåíò x1:
y (xm−1, xm−2, ... , x2, x1, x0) =
x 1] ∨ x0}½
= {[y (xm−1, xm−2, ... , x2, 0, 0) ∨ x1] ⋅ [y (xm−1, xm−2, ... , x2, 1, 0) ∨
½{[y (xm−1, xm−2, ... , x2, 0, 1) ∨ x1] ⋅ [y (xm−1, xm−2, ... , x2, 1, 1) ∨
x 1] ∨
x 0}.
Òåïåðü, èñïîëüçóÿ ôîðìóëó (2.3), îáîçíà÷èì ñîñòàâëÿþùèå,
çàêëþ÷åííûå â ïåðâûõ ôèãóðíûõ ñêîáêàõ ïîñëåäíåé ôîðìóëû,
ñëåäóþùèì îáðàçîì:
y (xm−1, xm−2, ... , x2, 0, 0) ∨ x1 = a;
y (xm−1, xm−2, ... , x2, 1, 0) ∨
x 1 = b;
x0 = c,
à âî âòîðûõ ôèãóðíûõ ñêîáêàõ
y (xm−1, xm−2, ... , x2, 0, 1) ∨ x1 = a;
x 1 = b;
y (xm−1, xm−2, ... , x2, 1, 1) ∨
x 0 = c.
Ïîñëå ÷åãî ïîëó÷èì ñëåäóþùåå âûðàæåíèå:
y (xm−1, xm−2, ... , x2, x1, x0) =
= [y(xm−1, xm−2, ... , x2, 0, 0) ∨ x1 ∨ x0]⋅[y(xm−1, xm−2, ... , x2, 1, 0) ∨
x 1 ∨ x0]½
x 0]⋅[y(xm−1, xm−2, ... , x2, 1, 1) ∨
x 1 ∨
x 0].
½[y(xm−1, xm−2, ... , x2, 0, 1) ∨ x1 ∨
Ðàñêðûâàÿ òàêèì îáðàçîì ïîñëåäîâàòåëüíî âñå îñòàëüíûå àðãóìåíòû, ïîëó÷èì îêîí÷àòåëüíîå âûðàæåíèå ôóíêöèè â ÑÊÍÔ:
X max
y (xm−1, xm−2, ... , x2, x1, x0) = ∧
X =0
[ yX
∨ Mx X ],
ãäå yX çíà÷åíèå ôóíêöèè â íàáîðå àðãóìåíòîâ X; MxX ìàêñòåðì, ò. å. äèçúþíêöèÿ âñåõ àðãóìåíòîâ ôóíêöèè, ïðè÷åì àðãó33
ìåíò â ïðÿìîé ôîðìå (xi), åñëè â äàííîì íàáîðå X îí ðàâåí íóëþ,
i) åñëè îí ðàâåí åäèíèöå.
è â èíâåðñíîé ôîðìå (x
Òåïåðü ïîñìîòðèì, êàêèìè ñâîéñòâàìè îáëàäàþò ìàêñòåðìû.
Äëÿ ýòîãî ñîñòàâèì èõ òàáëèöó èñòèííîñòè (òàáë. 2.9).
Îáðàòèòå âíèìàíèå íà òî, ÷òî êàæäûé ìàêñòåðì ñòàíîâèòñÿ
ðàâíûì íóëþ òîëüêî â îäíîì èç íàáîðîâ, à èìåííî â òîì, êîòîðîìó ñîîòâåòñòâóåò åãî íîìåð. Ýòî íàáëþäåíèå ïîçâîëÿåò ñäåëàòü
x
âûâîä î âçàèìîñâÿçè ìèíòåðìîâ è ìàêñòåðìîâ: MnX = M
X.
2.4. Ïðåäñòàâëåíèå ôóíêöèé ñ íå ïîëíîñòüþ çàäàííûìè
àðãóìåíòàìè â äèçúþíêòèâíîé íîðìàëüíîé ôîðìå
Áûâàþò ñëó÷àè, êîãäà ëîãè÷åñêàÿ ôóíêöèÿ ïðåäñòàâëåíà ñîêðàùåííîé òàáëèöåé èñòèííîñòè, è ïîýòîìó â íåêîòîðûõ åå ñòðîêàõ îòäåëüíûå àðãóìåíòû îêàçûâàþòñÿ çàäàííûìè ôàêóëüòàòèâíî.
 êà÷åñòâå ïðèìåðà ðàññìîòðèì ôóíêöèþ ïðèîðèòåòíîãî øèôðàòîðà, îïðåäåëÿþùåãî ñòàðøèé ðàçðÿä, â êîòîðîì íàõîäèòñÿ åäèíèöà, è ïðåîáðàçóþùåãî íîìåð ýòîãî ðàçðÿäà â íàòóðàëüíûé äâîè÷íûé êîä (òàáë. 2.10).
Äîêàæåì, ÷òî â ÄÍÔ ôóíêöèÿ äîëæíà áûòü ïðåäñòàâëåíà äèçúþíêöèåé èìïëèêàíò, âêëþ÷àþùèõ â ñåáÿ òîëüêî îïðåäåëåííûå
àðãóìåíòû:
y0 =
x 3 ⋅
x 2 ⋅ x1 ∨ x3; y1 =
x 3 ⋅ x2 ∨ x3.
Äëÿ óäîáñòâà ïîëíóþ òàáëèöó èñòèííîñòè ïðèîðèòåòíîãî øèôðàòîðà (òàáë. 2.11) ðàçäåëèì ïîëóæèðíûìè ãîðèçîíòàëüíûìè ëèíèÿìè íà ñåêòîðû ñ îäèíàêîâûì ðàñïîëîæåíèåì ñòàðøèõ åäèíèö
àðãóìåíòîâ.
Ïðîèçâåäåì ñ÷èòûâàíèå ôóíêöèè â ÑÄÍÔ ñ ïîñëåäóþùèì
ñêëåèâàíèåì ñîñåäíèõ (ñîïðÿæåííûõ) ìèíòåðìîâ è èìïëèêàíò:
Ò à á ë è ö à 2.9
Òàáëèöà èñòèííîñòè
ìàêñòåðìîâ
Àðãóìåíòû
Ò à á ë è ö à 2.10
Òàáëèöà èñòèííîñòè ïðèîðèòåòíîãî
øèôðàòîðà
Ìàêñòåðìû
N3
N2
N1
N0
O1
O0
Mx0 Mx1 Mx2 Mx3
0
0
0
0
*
*
:
N1
N0
0
0
0
0
1
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
0
0
1
*
0
1
2
1
0
1
1
0
1
0
1
*
*
1
0
3
1
1
1
1
1
0
1
*
*
*
1
1
34
Ò à á ë è ö à 2.11
Ïîëíàÿ òàáëèöà èñòèííîñòè ïðèîðèòåòíîãî øèôðàòîðà
n
x3
x2
x1
x0
y1
y0
0
0
0
0
0
*
*
1
0
0
0
1
0
0
2
0
0
1
0
0
1
3
0
0
1
1
0
1
4
0
1
0
0
1
0
5
0
1
0
1
1
0
6
0
1
1
0
1
0
7
0
1
1
1
1
0
8
1
0
0
0
1
1
9
1
0
0
1
1
1
10
1
0
1
0
1
1
11
1
0
1
1
1
1
12
1
1
0
0
1
1
13
1
1
0
1
1
1
14
1
1
1
0
1
1
15
1
1
1
1
1
1
y0 =
x 3 ⋅
x 2 ⋅ x1 ⋅
x0 ∨
x 3 ⋅
x 2 ⋅ x1 ⋅ x0 ∨ x3 ⋅
x 2 ⋅
x 1 ⋅
x 0 ∨ x3 ⋅
x 2 ⋅
x 1 ⋅ x0 ∨ x 3 ⋅
x 2 ⋅ x1 ⋅
x0 ∨
x 2 ⋅ x 1 ⋅ x0 ∨ x 3 ⋅ x2 ⋅
x 1 ⋅
x 0 ∨ x3 ⋅ x 2 ⋅
x 1 ⋅ x 0 ∨ x 3 ⋅ x 2 ⋅ x1 ⋅
x 0 ∨ x 3 ⋅ x2 ⋅ x 1 ⋅ x 0 =
∨ x3 ⋅
0 ∨ x0) ∨ x3 ⋅
0 ∨ x0) ∨ x3 ⋅
0 ∨ x0) ∨
x 2 ⋅ x1 ⋅ (x
x 2 ⋅
x 1 ⋅ (x
x 2 ⋅ x1 ⋅ (x
=
x 3 ⋅
0 ∨ x0) ∨ x3 ⋅ x2 ⋅ x1 ⋅ (x
0 ∨ x0) =
x 1 ⋅ (x
∨ x 3 ⋅ x2 ⋅
=
x 3 ⋅
x 2 ⋅ x1 ∨ x3 ⋅
x 2 ⋅
x 1 ∨ x3 ⋅
x 2 ⋅ x 1 ∨ x 3 ⋅ x2 ⋅
x 1 ∨ x 3 ⋅ x2 ⋅ x 1 =
1 ∨ x1) ∨ x3 ⋅ x2 ⋅ (x
1 ∨ x1) =
x 2 ⋅ x1 ∨ x3 ⋅
x 2 ⋅ (x
=
x 3 ⋅
x 2 ⋅ x 1 ∨ x3 ⋅
x 2 ∨ x3 ⋅ x2 =
=
x 3 ⋅
2 ∨ x2) =
x 2 ⋅ x1 ∨ x3 ⋅ (x
x 3 ⋅
x 2 ⋅ x1 ∨ x3.
=
x 3 ⋅
Ïîñêîëüêó ïîñëåäíèå âîñåìü ìèíòåðìîâ ó îáåèõ ôóíêöèé îäèíàêîâûå, ïðèâåäåì äëÿ y1 ñðàçó óïðîùåííûé âàðèàíò çàïèñè:
35
x 3 ⋅ x2 ⋅
x 1 ⋅
x0 ∨
x 3 ⋅ x2 ⋅
x 1 ⋅ x0 ∨
x 3 ⋅ x2 ⋅ x 1 ⋅
x0 ∨
x 3 ⋅ x2 ⋅ x 1 ⋅ x 0 ∨ x3 =
y1 =
0 ∨ x0) ∨
0 ∨ x0) ∨ x3 =
x 1 ⋅ (x
x 3 ⋅ x2 ⋅ x1 ⋅ (x
=
x 3 ⋅ x2 ⋅
1 ∨ x1) ∨ x3 =
=
x 3 ⋅ x2 ⋅
x1 ∨
x 3 ⋅ x2 ⋅ x1 ∨ x3 =
x 3 ⋅ x2 ⋅ (x
x 3 ⋅ x 2 ∨ x3 .
Ýòî è òðåáîâàëîñü äîêàçàòü.
Ïîëó÷åííûå âûðàæåíèÿ ìîæíî åùå áîëåå óïðîñòèòü, åñëè èñïîëüçîâàòü ðàññìîòðåííûé â ãë. 1 ïðèåì:
a∨
a ⋅ b = a ⋅ (1 ∨ b) ∨
a ⋅b = a ∨ a⋅b ∨
a ⋅ b = a ∨ (a ∨
a ) ⋅ b = a ∨ b.
Îêîí÷àòåëüíî íàõîäèì: y0 = x3 ∨
x 2 ⋅ x1; y1 = x3 ∨ x2.
Êîíòðîëüíûå âîïðîñû
1. ×òî òàêîå ìèíòåðì è êàêîâû åãî ñâîéñòâà?
2. Êàê âûðàæàåòñÿ ëîãè÷åñêàÿ ôóíêöèÿ â ÑÄÍÔ?
3. ×òî òàêîå ñîñåäíèå ìèíòåðìû?
4. ×òî òàêîå èìïëèêàíòû è êàê îíè ïîëó÷àþòñÿ?
5. Èç êàêèõ ýòàïîâ ñîñòîèò ïðîöåäóðà ìèíèìèçàöèè ëîãè÷åñêèõ ôóíêöèé?
6. Êàê ìèíèìèçèðîâàòü ôóíêöèþ ïðåîáðàçîâàòåëÿ êîäà «1 èç 4» â íàòóðàëüíûé äâîè÷íûé êîä?
7. Ñôîðìóëèðóéòå è äîêàæèòå òåîðåìó Øåííîíà î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé äèçúþíêöèåé äâóõ êîíúþíêöèé.
8. Äîêàæèòå òåîðåìó î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé â ÑÄÍÔ.
9. Ñîñòàâüòå òàáëèöó èñòèííîñòè äëÿ êîäà «1 èç 4».
10. Ñîñòàâüòå òàáëèöó èñòèííîñòè äëÿ øèôðàòîðà ïðåîáðàçîâàòåëÿ
êîäà «1 èç 4» â íàòóðàëüíûé äâîè÷íûé êîä.
11. Çàïèøèòå â ÑÄÍÔ ëîãè÷åñêóþ ôóíêöèþ, ñîîòâåòñòâóþùóþ äèçúþíêöèè äâóõ ïåðåìåííûõ.
12. ×òî íàçûâàåòñÿ ñîêðàùåííîé ÄÍÔ?
13. Êàêàÿ ôîðìà ÄÍÔ íàçûâàåòñÿ òóïèêîâîé?
14. Êàêàÿ ÄÍÔ ëîãè÷åñêîé ôóíêöèè íàçûâàåòñÿ ìèíèìàëüíîé?
15. Ñîñòàâüòå òàáëèöó èñòèííîñòè êîäà Ãðåÿ.
16. Çàïèøèòå â ÑÄÍÔ è ìèíèìèçèðóéòå ðàçðÿäíûå ôóíêöèè êîäà
Ãðåÿ.
17. Êàêàÿ èç ÷åòûðåõ ïðèâåäåííûõ ôóíêöèé ÿâëÿåòñÿ ìèíòåðìîì:
1)
x
0 ⋅ x 1 ∨ x2 ⋅ x3; 2) x0 ∨ x1 ∨ x2 ∨ x3; 3) x0 ⋅ x 1 ⋅ x2 ⋅ x3; 4) x0 ∨ x1 ∨ x2 ∨ x3?
18. Êàê âëèÿåò íà ñëîæíîñòü ìèíèìèçèðîâàííîé ôóíêöèè íàëè÷èå
çàïðåùåííûõ êîìáèíàöèé (íå âëèÿåò; óïðîùàåò; óñëîæíÿåò)?
19. Ñôîðìóëèðóéòå è äîêàæèòå òåîðåìó î ïðåäñòàâëåíèè ëîãè÷åñêèõ
ôóíêöèé êîíúþíêöèåé äâóõ äèçúþíêöèé.
20. Äîêàæèòå òåîðåìó î ïðåäñòàâëåíèè ëîãè÷åñêèõ ôóíêöèé â ÑÊÍÔ.
21. Çàïèøèòå â ÑÊÍÔ ëîãè÷åñêóþ ôóíêöèþ, ñîîòâåòñòâóþùóþ êîíúþíêöèè äâóõ ïåðåìåííûõ.
22. Âûâåäèòå ôóíêöèè äëÿ ÷åòûðåõðàçðÿäíîãî ïðåîáðàçîâàòåëÿ íàòóðàëüíîãî äâîè÷íîãî êîäà â êîä Ãðåÿ.
36