1 Преобразование графиков функций
реклама

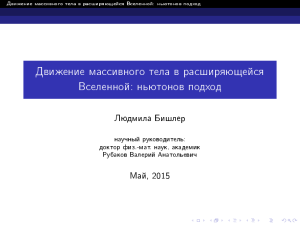
ÂØÝ, 2011-12, ¾Äîïîëíèòåëüíûå ãëàâû àëãåáðû è àíàëèçà¿ Ôàêóëüòåò ïðèêëàäíîé ïîëèòîëîãèè, 2011-12 ó÷. ãîä. Äîïîëíèòåëüíûå ãëàâû àëãåáðû è àíàëèçà Çàäà÷è äëÿ òðåíèðîâêè 1 (22 ñåíòÿáðÿ 2013 ã.) È. À. Õîâàíñêàÿ, È. Â. Ùóðîâ, Þ. Ã. Êóäðÿøîâ, Ï. Ô. Ñîëîìàòèí, Ê. È. Ñîíèí (ÐÝØ) 1 Ïðåîáðàçîâàíèå ãðàôèêîâ ôóíêöèé y 1 0 x 1 Ðèñ. 1: Ðèñóíîê ê çàäà÷å 1 Çàäà÷à 1. Íà ðèñóíêå 1 èçîáðàæåí ãðàôèê ôóíêöèè y = f (x). Ïóñòü g(x) = f (3x). ×òîáû ïîñòðîèòü ãðàôèê ôóíêöèè y = g(x), ñäåëàéòå ñëåäóþùåå: (a) Ïî ãðàôèêó, íàéäèòå (ïðèìåðíî) çíà÷åíèå ôóíêöèè 3. Ñîñòàâüòå òàáëèöó çíà÷åíèé f f â òî÷êàõ −3, −2, −1, 0, 1, 2, â ýòèõ òî÷êàõ. Îòìåòüòå ñîîòâåòñòâóþùèå òî÷êè íà ãðàôèêå. (b) Çàìåòèì, ÷òî g(1) = f (3·1) = f (3). Íàéäèòå çíà÷åíèå g(1). Îòìåòüòå ñîîòâåòñòâóþùóþ y = g(x). Íàïîìèíàíèå. Òî÷êà, ñîîòâåòñòâóþùàÿ çíà÷åíèþ g(1) áóäåò èìåòü êîîðäèíàòó x, ðàâíóþ 1 (àðãóìåíòó ôóíêöèè) è êîîðäèíàòó y , ðàâíóþ g(1) (çíà÷åíèþ ôóíêöèè). Íàéäèòå çíà÷åíèå g(−1). Îòìåòüòå ñîîòâåòñòâóþùóþ òî÷êó íà ãðàôèêå ôóíêöèè y = g(x). Çàìå÷àíèå. Ìû ìîãëè áû ïîñòðîèòü òî÷êó, ñîîòâåòñòâóþùóþ g(1), íå íàõîäÿ ÷èñëåííîãî çíà÷åíèÿ f (3). Äåéñòâèòåëüíî, ïîñìîòðèì íà òî÷êó, ñîîòâåòñòâóþùóþ f (3) íà ãðàôèêå y = f (x) (ïóñòü ýòî òî÷êà A). Òî÷êà, ñîîòâåòñòâóþùàÿ g(1) (ïóñòü ýòî òî÷êà B ), äîëæíà èìåòü òàêóþ æå y -êîîðäèíàòó, òî åñòü ëåæàòü íà òîé æå ãîðèçîíòàëüíîé ïðÿìîé, îäíàêî å¼ x-êîîðäèíàòà äîëæíà áûòü ðàâíà 1, à íå 3. Òî åñòü ÷òîáû ïîëó÷èòü òî÷êó B íà ãðàôèêå y = g(x), íóæíî ñîîòâåòñòâóþùóþ òî÷êó A íà ãðàôèêå y = f (x) ñäâèíóòü ê îñè Oy , óìåíüøèâ å¼ y -êîîðäèíàòó âòðîå. òî÷êó, ëåæàùóþ íà (åùå íå ïîñòðîåííîì) ãðàôèêå ôóíêöèè (c) È. À. Õîâàíñêàÿ, È. Â. Ùóðîâ, Þ. Ã. Êóäðÿøîâ, Ï. Ô. Ñîëîìàòèí, Ê. È. Ñîíèí (ÐÝØ) 1 ÂØÝ, 2011-12, ¾Äîïîëíèòåëüíûå ãëàâû àëãåáðû è àíàëèçà¿ (d) Äëÿ êàêèõ çíà÷åíèé x ìû ìîæåì íàéòè çíà÷åíèå g(x) ïî òàáëèöå, ïîñòðîåííîé â ïóíêg(x) â ýòèõ òî÷êàõ. Ïîñòðîéòå ñîîòâåòñòâóþùèå òî÷êè íà y = g(x). Êàêèå òî÷êè ñ ãðàôèêà f (x) ïåðåõîäÿò â ïîñòðîåííûå òî÷êè? Êàê òå 1a? Íàéäèòå çíà÷åíèÿ ãðàôèêå ìåíÿþòñÿ èõ êîîðäèíàòû? Êàê ìåíÿåòñÿ âåñü ãðàôèê ôóíêöèè? (e) Ïîñòðîéòå ãðàôèê ôóíêöèè y = g(x). Çàäà÷à 2. Äëÿ òîé æå ôóíêöèè f (x), ïîñòðîèòü ãðàôèêè ñëåäóþùèõ ôóíêöèé (ïðè íåîáõî- äèìîñòè, ïðîâåäèòå òàêîé æå àíàëèç, êàê è â ïðåäûäóùåé çàäà÷å: íàéäèòå çíà÷åíèå ôóíêöèè f (x) â íåñêîëüêèõ òî÷êàõ, ïðîàíàëèçèðóéòå, çíà÷åíèå ôóíêöèè g(x) â êàêèõ òî÷êàõ ìîæíî íàéòè, èñïîëüçóÿ âû÷èñëåííûå çíà÷åíèÿ; íàéäèòå èõ, ïîñòðîéòå ñîîòâåòñòâóþùèå òî÷êè íà ãðàôèêàõ y = f (x) è y = g(x), óñòàíîâèòå, êàê ñâÿçàíû êîîðäèíàòû ýòèõ òî÷åê, è ÷òî ïðîèñõîäèò ñ ãðàôèêîì). (a) (b) (c) (d) (e) (f) (g) (h) (i) 2 y y y y y y y y y = f (3x); = 3f (x); = f (x)/3; = f (3x) + 2; = f (3x + 2); = f (x/3 − 3); = 3f (x) + 1; = 3f (x + 1); = 3f (x/2 − 1). Ïðåäåëû è íåïðåðûâíîñòü Çàäà÷à 3. Ðàññìîòðèì ôóíêöèþ ( 2x + 1, x < 0 f (x) = −x2 + 1, x ≥ 0 (a) Íàéòè çíà÷åíèå ôóíêöèè f (x) â òî÷êàõ x = −2, −1, 0, 1, 2. (b) Ïîñòðîéòå ãðàôèê ýòîé ôóíêöèè. (c) Íàéäèòå ïðåäåëû, åñëè îíè ñóùåñòâóþò: limx→1+ f (x), limx→1− f (x) , limx→1 f (x), limx→0+ limx→0− f (x), limx→0 f (x). f (x) (d) ßâëÿåòñÿ ëè ôóíêöèÿ íåïðåðûâíîé â òî÷êå f (x), 0? Çàäà÷à 4. Ðàññìîòðèì ôóíêöèþ ( x3 , x < 0 f (x) = x2 − 1, x ≥ 0 (a) Íàéòè çíà÷åíèå ôóíêöèè f (x) â òî÷êàõ x = −2, −1, 0, 1, 2. (b) Ïîñòðîéòå ãðàôèê ýòîé ôóíêöèè. (c) Íàéäèòå ïðåäåëû, åñëè îíè ñóùåñòâóþò: limx→1+ f (x), limx→1− f (x) , limx→1 f (x), limx→0+ limx→0− f (x), limx→0 f (x). f (x) (d) ßâëÿåòñÿ ëè ôóíêöèÿ íåïðåðûâíîé â òî÷êå 0? È. À. Õîâàíñêàÿ, È. Â. Ùóðîâ, Þ. Ã. Êóäðÿøîâ, Ï. Ô. Ñîëîìàòèí, Ê. È. Ñîíèí (ÐÝØ) 2 f (x), ÂØÝ, 2011-12, ¾Äîïîëíèòåëüíûå ãëàâû àëãåáðû è àíàëèçà¿ 3 Ýêñïîíåíòà è ëîãàðèôì Çàäà÷à 5.  ïðîöåññå ðàäèîàêòèâíîãî ðàñïàäà êîëè÷åñòâî íåêîòîðîãî ðàäèîàêòèâíîãî âåùåñòâà óìåíüøàåòñÿ âäâîå êàæäûå 10 ëåò (ýòî òàê íàçûâàåìûé ¾ïåðèîä ïîëóðàñïàäà¿). Èçâåñòíî, ÷òî 1 ÿíâàðÿ 2010 ãîäà ýòîãî âåùåñòâà â íåêîòîðîì êîíòåéíåðå ñîñòàâëÿëî 400 ã. Áóäåì ñ÷èòàòü, ÷òî ýòî âåùåñòâî áûëî ïîìåùåíî â êîíòåéíåð êîãäà-òî î÷åíü äàâíî, è ñ ýòîãî ìîìåíòà êîíòåéíåð íèêòî íå îòêðûâàë, è íèêîãäà íå áóäåò îòêðûâàòü. (a) Ñêîëüêî âåùåñòâà áûëî â êîíòåéíåðå â 2000 ãîäó (íà íà÷àëî ãîäà)?  1990 ãîäó? (b) Ñêîëüêî âåùåñòâà áóäåò â êîíòåéíåðå â 2020 ãîäó?  2030 ãîäó? (c) Ïóñòü â íà÷àëå ãîäà (d) t â êîíòåéíåðå áûëî f (t) ãðàìì âåùåñòâà. Èç óñëîâèÿ ñëåäóåò, ÷òî f (2010) = 400. Âûïèñàòü ôîðìóëó äëÿ f (t) äëÿ ïðîèçâîëüíîãî ãîäà t. Âûïèñàòü ôîðìóëó äëÿ ôóíêöèè f −1 (x), îáðàòíîé ê ôóíêöèè f (t). (e)  êàêîé ìîìåíò âðåìåíè (ïðèìåðíî) â êîíòåéíåðå áóäåò 1600 ã âåùåñòâà? 2 êã âåùåñòâà? È. À. Õîâàíñêàÿ, È. Â. Ùóðîâ, Þ. Ã. Êóäðÿøîâ, Ï. Ô. Ñîëîìàòèí, Ê. È. Ñîíèí (ÐÝØ) 3