10 кл. Система оценивания по математике 2012 г.
реклама

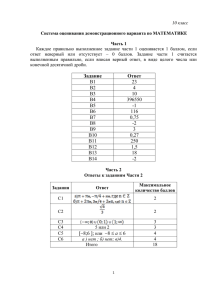
Система оценивания демонстрационного варианта по МАТЕМАТИКЕ Часть 1 Каждое правильно выполненное задание части 1 оценивается 1 баллом, если ответ неверный или отсутствует – 0 баллов. Задание части 1 считается выполненным правильно, если вписан верный ответ. № задания Ответ В1 12 В2 -2 В3 -5 В4 53 В5 2,25 В6 6 В7 12 В8 0,75 В9 128 В10 4000 В11 243 В12 15 В13 0,92 Часть 2 Ответы к заданиям Части 2 Задания Ответ Максимальное количество баллов С1 2 2n; , n Z 3 2 С2 С3 С4 С5 С6 2 3 х = -0,25 7 2 ;1 2; 4 1 и 1045 Итого 3 4 4 18 Решения и критерии оценивания заданий с развёрнутым ответом Оценки заданий части 2 зависят от полноты решения и правильности ответа. Общие требования к выполнению заданий с развернутым ответом: решение должно быть математически грамотным, полным, из него должен быть понятен ход рассуждений учащегося, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. Если решение ученика удовлетворяет этим требованиям, то ему, в зависимости 1 от полноты и правильности выполнения, выставляется определенное критериями количество баллов. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов. В критериях оценивания конкретных заданий содержатся общие требования к выставлению баллов. Однако они не исчерпывают всех возможных ситуаций. 2 sin 2 x 5 sin x 0, С1. Решите систему уравнений 6 y 2 cos x 0. Решение: Пусть sin x = t. Тогда первое уравнение примет вид 2t2 - 5t = 0, откуда t = 0 или t = 2,5. Уравнение sin x = 2,5 не имеет корней, так как sin x 1;1 Из второго уравнения системы следует, что cos x 0. Тогда из уравнения sin x = 0 получаем: х = 2 n, n Z и cos x = 1. Второе уравнение примет вид 6 y 2 0 , откуда y = 2 . 3 2 3 Ответ: 2n; , n Z. Возможна другая форма записи ответа: х = 2 n, n Z, y = 2 . 3 Содержание критерия Баллы Обоснованно получен правильный ответ 2 Получен ответ, но решение неверно только из-за того, что не учтены 1 ограничения на знак или величину выражения cosx (sinx) Другие случаи, не соответствующие перечисленным выше критериям 0 Максимальный балл 2 С2. Докажите, что диаметр окружности, проведённый через середину хорды (не являющейся диаметром), перпендикулярен этой хорде. Решение: OE - медиана треугольника COD. Так как OC = OD, треугольник COD равнобедренный. Следовательно, OE является высотой треугольника COD. Поэтому AB CD. Содержание критерия 2 Баллы Выполнен верный чертёж, ход доказательства верный, все его шаги выполнены правильно Выполнен верный чертёж, доказательство содержит неточности Другие случаи, не соответствующие перечисленным выше критериям Максимальный балл 2 1 0 2 С3. Решите уравнение 2x 3 4x 5 6x 1 . Решение: Данное уравнение равносильно трём системам: х 1,25, 1,25 х 1,5, х 1,5, (1) (2) (3) 3 2 х (5 4 х) 6 х 1. 3 2 х (4 х 5) 6 х 1. 2 х 3х (4 х 5 х) 6 х 1. Решая уравнение из системы удовлетворяет условию х 1,25. получаем х=-0,25. Корень уравнения Решая уравнение из системы (2) получаем не удовлетворяет условию 1,25< х 1,5. х=0,75. Корень уравнения х=0,375. Корень уравнения Решая уравнение из системы не удовлетворяет условию х > 1,5. (1) (3) получаем Ответ: х=-0,25. Содержание критерия Баллы Обоснованно получен правильный ответ 3 Получен ответ, но в записи допущена погрешность, которая может быть 2 расценена как описка Получен ответ, отличающийся от верного наличием посторонних корней 1 Другие случаи, не соответствующие перечисленным выше критериям 0 Максимальный балл 3 С4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки C до прямой A1B1. Решение: Искомое расстояние равно расстоянию от прямой A1B1 до параллельной ей прямой FС. 3 Опустим из точки A1 перпендикуляр A1М на прямую FС. Точка М лежит в плоскости AA1E1, перпендикулярной прямой FС. Поэтому точка М лежит на пересечении АЕ и FС, а значит, является серединой АЕ. В AFE F =1200. По теореме косинусов: АЕ2 = 12 + 12 - 2 1 1 cos 1200. Значит, АЕ= 3 , АМ= 3 . Из прямоугольного треугольника АA1М получаем 2 2 3 7 A1М= 12 . 2 2 Ответ: 7 . 2 Содержание критерия Баллы Обоснованно получен правильный ответ 3 Способ нахождения искомого расстояния верен, но получен неверный 2 ответ только из-за вычислительной ошибки Искомое расстояние указано верно, но решение по его нахождению 1 не закончено Другие случаи, не соответствующие перечисленным выше критериям 0 Максимальный балл 3 С5. Решите неравенство: х 2 6х 8 х4 2 0. х 1 х 3х 2 Решение: Разложим квадратные трёхчлены на множители: ( х 2)( х 4) х4 0; х 1 ( х 1)( х 2) х4 1 х2 0; х 1 х 2 ( х 4)(( х 2) 2 1) х4 0. 0; (х-2)2+1>0 при всех х. Следовательно, ( х 1)( х 2) ( х 1)( х 2) 4 Решая методом интервалов, получаем х < 1 или 2 < x 4. Ответ: ;1 2; 4 Содержание критерия Баллы Обоснованно получен правильный ответ 4 Получен ответ, отличающийся от верного только конечным числом точек 3 Получен один из верных промежутков 2 Ход решения верный, но допущены ошибки 1 Другие случаи, не соответствующие перечисленным выше критериям 0 Максимальный балл 4 С6. Перед каждым из чисел 2, 3, …, 6 и 10, 11, …, 20 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 55 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге? Решение: 1. Если все числа взяты со знаком плюс, то их сумма максимальна и равна 2 6 10 20 5 +5 11 =55 19 =1045. 2 2 11(2+…+6)+5(10+…+20)=11 2. Так как предыдущая сумма оказалась нечетной, то число нечетных слагаемых в ней – нечётно, причём это свойство всей суммы не меняется при смене знака любого её слагаемого. Поэтому любая из получающихся сумм будет нечётной, а значит, не будет равна 0. 3. Значение 1 сумма принимает, например, при следующей расстановке знаков у чисел: 11(−2 + 3 − 4 + 5 − 6) + 5(10 + 11 − 12 − 13 + 14 + 15 − 16 − 17 + 18 + 19 − 20) = = −11 · 4 + 5 · 9 = − 44 + 45 = 1. Ответ: 1 и 1045. Содержание критерия Баллы Обоснованно получен правильный ответ 4 Ответ правилен, но недостаточно обоснован (например, не доказано, 3 что либо сумма отлична от 0, либо что она может быть равна 1) Верно найдено наибольшее значение суммы и доказано, что она всегда 2 отлична от 0 Верно найдено только наибольшее значение суммы или только доказано, 1 что она всегда отлична от 0 Другие случаи, не соответствующие перечисленным выше критериям 0 Максимальный балл 4 5