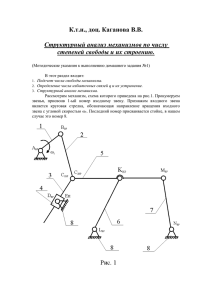
2. Структурный анализ механизмов

СТРУКТУРА И КИНЕМАТИКА МЕХАНИЗМОВ
2. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ
2.1. Кинематические пары и их классификация
2.1.1. Связи
Связью называют ограничение, стесняющее движения рассматриваемого
тела (звена механизма), осуществляемое другими телами или материальными
объектами (окружающая среда, промежуточные элементы, рабочие
тела,
звенья и др.).
Твердое тело, движения которого не ограничены связями, называют
свободным, а при их наличии − не свободным.
Связи описываются их уравнениями. Различают голономные (конечные)
и неголономные связи. Голономные связи ограничивают только свободу
взаимного перемещения тел и не зависят от времени. Примерами таких связей
являются геометрические связи (рис. 9, г; 10, а, в; 11, в). Уравнения таких
связей выражаются аналитически конечными соотношениями между координатами точек системы. Неголономные связи налагают ограничения на перемещение и скорость точек системы. Например, в паре шар − плоскость (рис. 9, а)
шар может перекатываться и скользить по плоскости. В этом случае связь
выражается уравнением z s = r (расстояние от центра шара до плоскости
постоянно и равно радиусу r). Если шар будет перекатываться по плоскости без
проскальзывания, то, кроме условия z s = r , накладывается еще одно −
скорость точки касания шара и плоскости равна нулю. Такие связи называются
кинематическими.
а
б
в
г
Рис. 9
Пример динамической связи − контакт приводного ролика и магнитной
ленты (МЛ). Здесь дополнительная динамическая связь появляется за счет сил
трения.
Связь может быть прерываемой, как это отмечается в местах соединения
зуба храпового колеса с «собачкой» или пальца с пазом мальтийского креста в
механизмах, для старт-стопного перемещения носителей.
Кроме изложенных связей, на звенья механизма воздействует
окружающая среда (масса, сопротивление воздуха), рабочие тела (газы,
жидкости, упругие элементы, обрабатываемые или перемещаемые объекты и
др.).
2.1.2. Кинематические пары
Кинематической парой называют совокупность поверхностей, линий или
точек, по которым происходит подвижное соединение двух звеньев.
Поверхность, линия или точка, которыми данное звено соприкасается
с другим звеном, называется элементом кинематической пары.
В зависимости от вида элементов различают низшие и высшие
кинематические пары. Элементами высших пар являются линии или точки:
точка соприкосновения шара и плоскости (рис. 9, а); линия соприкосновения
цилиндра и плоскости (рис. 9, б); линия соприкосновения паза молоточка и
упругого элемента, кулачка 1 и рычага 2, зубьев зубчатых колес 1 и 2 (рис. 11,
а−в). Элементами низших пар служат поверхности: соприкосновения
параллелепипеда и плоскости, шара и шарообразного углубления (рис. 9, в, г);
цилиндрические поверхности рычагов 1 и 2 с осью, пуансона 1 и матрицы О
(рис. 10, а, в).
а
в
б
г
Рис. 10
а
б
Рис. 11
а
в
б
Рис. 12
При обращении одного звена пары в стойку можно определить вид
траектории отдельных точек подвижного звена относительно неподвижного
(стойки). Если эти траектории являются плоскими кривыми, лежащими в
параллельных плоскостях, то такие пары являются плоскими (рис. 10, 11).
Низшие кинематические пары обратимы: вид траекторий подвижного звена
относительно стойки не меняется при обращении подвижного звена в стойку.
Относительное движение звеньев низших пар сопровождается скольжением их
элементов, что вызывает их износ и потери мощности на трение.
Положительное свойство низших пар − их относительно большая по сравнению
с высшими несущая способность.
Существенным отличием высших КП является их необратимость
(рис. 12, б): при обращении звена 1 в стойку точка А2 звена 2 описывает
эвольвенту, а при обращении в стойку звена 2 точка А1 звена 1 описывает
циклоиду. Относительное движение звеньев высшей пары может
сопровождаться качением или качением с проскальзыванием. Из-за малости
поверхностей контакта потери мощности на трение в высших парах меньше,
чем
в низших, но удельное давление больше.
Замыкание кинематических пар может быть геометрическим
(рис. 9, г; 10; 11, а, б; 12, а) или силовым (рис. 9, а, б; 11, а, б). Силовое
замыкание может осуществляться силами сопротивления (рис. 11, в) либо
силами, создаваемыми упругими элементами.
2.1.3. Классификация кинематических пар
Форма элементов кинематических пар и их взаимное расположение
определяют вид и количество независимых относительных движений звеньев.
В зависимости от количества наложенных связей различают пять классов
кинематических пар. Свободное твердое тело (звено) в пространстве имеет
шесть независимых движений (степеней свободы).
Класс кинематической пары определяет число условий связи, налагаемых
на относительное движение звеньев. Если Н − число степеней свободы
элемента кинематической пары относительно стойки, то
S = 6 − H.
(2.1)
Например, в парах: первого (рис. 9, а) Н = 5, S = l и второго класса
(рис. 9, б) Н = 4, S = 2; третьего класса (рис. 9, в, г) Н = 3, S = 3; четвертого
класса (рис. 11, а−в) Н = 2, S = 4; пятого класса (рис. 10, а−г) H =l, S =5.
2.2. Кинематические цепи. Механизм
Совокупность звеньев, соединенных кинематическими парами, называют
кинематической цепью. Кинематические цепи бывают простыми, если каждое
звено входит не более, чем в две кинематические пары (рис. 13, а); замкнутыми
и незамкнутыми, если есть звенья, входящие только в одну кинематическую
пару.
а
б
Рис. 13
в
Различают пространственные и плоские кинематические цепи. В
пространственных цепях точки разных звеньев описывают неплоские или
плоские траектории, но лежащие в непараллельных плоскостях. Плоской
называют кинематическую цепь, звенья которой расположены в параллельных
плоскостях и совершают плоские движения. Поскольку на звенья плоских
цепей наложены три условия связи, то в их состав могут входить только пары
четвертого и пятого классов.
Механизмом называют кинематическую цепь, в которой при задании
движения одному или нескольким звеньям относительно стойки остальные
звенья совершают вполне определенные движения. В механизмах чаще
используются замкнутые кинематические цепи, однако в механизмах
управления могут использоваться и незамкнутые.
Звенья, движения которых заданы, называют ведущими, остальные −
ведомыми. При анализе механизмов иногда задают движение не ведущим
звеньям, на которые действуют движущие силы, а другим. Такие звенья
называют входными. Исследуемые звенья кинематической цепи, движение
которых является производным от положения входных, называют выходными.
2.3. Подвижность механизмов
Одна из основных задач структурного анализа механизмов − определение
их подвижности и числа ведущих звеньев. Звено плоской кинематической цепи
имеет три степени свободы. Если в составе кинематической цепи n подвижных
звеньев, то число ее степеней свободы будет 3n. Каждая кинематическая пара
пятого класса налагает два ограничения (условия связи) на относительное
движение звеньев. Если количество пар пятого класса − Р5, то число условий
связи, налагаемых всеми парами пятого класса − 2Р5. Каждая кинематическая
пара четвертого класса налагает одно ограничение на относительное движение
звеньев. Если количество пар четвертого класса − Р4, то число условий связи,
налагаемых всеми парами четвертого класса − Р4. Число условий связи,
налагаемое совместно парами четвертого и пятого классов на относительное
движение звеньев, 2Р5 + Р4. Если W − число степеней свободы (степень
подвижности) кинематической цепи, то
W = 3n − 2P5 − P4.
(2.2)
Количество ведущих звеньев соответствует степени подвижности
механизма W, т. е. числу степеней свободы относительно стойки. Формула (2.2)
впервые была получена П. Л. Чебышевым и носит его имя.
В периферийных устройствах встречаются механизмы, действительная
степень подвижности которых не удовлетворяет условию (2.2) вследствие
наличия пассивных условий связи или пассивных подвижностей. В механизмах
шарнирного параллелограмма (рис. 13, а) и эллипсографа (рис. 13, б) с одной
степенью свободы пассивные условия связи появились в результате
присоединения звена 4. Эти звенья не изменяют кинематики механизма, но
уменьшают степень свободы на единицу: W = 3n − 2P5 = 3⋅4 − 2 − 6 = 0. Но если
АВ = CD = O1O3 для механизма (рис. 13, б) и АВ = ВС и направления движения
ползунов 3 и 4 проходят через точку О для механизма (рис. 13, б), то
фактическая степень подвижности W = l. Такие звенья называют пассивными и
вводят для увеличения жесткости, лучшего распределения нагрузки, создания
определенности направления движения и т. п.
В механизме (рис. 13, в) со степенью подвижности кинематической
цепи W = 3n − 2P5 − P4 = 3⋅3 − 2 − 3 = 2 «лишний» ролик 2 создает пассивную
подвижность и введен для улучшения условий работы. При определении
степени подвижности механизмов пассивные условия связаны и подвижности
условно исключают.
а
б
Рис. 14
Для удобства классификации плоских механизмов и решения некоторых
других задач высшие пары четвертого класса условно заменяют цепями,
содержащими только низшие пары пятого класса. Заменяющие цепи должны
быть структурно и кинематически эквивалентными высшим парам.
Эквивалентная кинематическая цепь, заменяющая одну пару четвертого
класса, содержит одно звено или две пары пятого класса.
Замена высших пар четвертого класса цепями с низшими парами пятого
класса выполняется в такой последовательности (рис. 14, а):
проводят нормаль к профилям звеньев в точках их контакта;
определяют положение центров кривизны профилей;
устанавливают в центрах кривизны вращательные пары пятого класса;
соединяют полученные пары между собой и соответствующим звеньями
(штриховые линии на рис. 14, а, б).
Если один из профилей представляет прямую (центр кривизны удален
в бесконечность), то вместо вращательной пары образуется поступательная.
2.4. Структурная классификация механизмов
Структурная классификация плоских механизмов с кинематическими
парами пятого класса разработана академиком И. И. Артоболевским на основе
идей Л. В. Ассура. В основу классификации Ассура − Артоболевского положен
следующий принцип: сложные механизмы образуются присоединением
к простейшему механизму, состоящему из стойки и одного подвижного звена
(рис. 15), кинематических цепей, обладающих нулевой подвижностью.
Кинематическая цепь, которая, будучи присоединенной свободными
элементами пар к стойке, обладает нулевой подвижностью, и называется
группой Ассура.
а
б
Рис. 15
в
Простейший механизм (рис. 16), согласно структурной классификации
Ассура − Артоболевского, относится к первому классу и имеет
W =3n − 2Р5 = 3⋅1 − 2⋅1 = 1.
Из условия существования группы
W = 3n − 2P5 = 0
(2.3)
3
2
получаем P5 = n .
Таким образом, в состав структурной группы может входить количество
звеньев, кратное 2, и число кинематических пар пятого класса, кратное 3.
Простейшая группа представляет собой простую кинематическую цепь,
состоящую из двух подвижных звеньев и трех кинематических пар (рис. 16, а−д).
Такие группы называют двухповодковыми, или диадами, и по классификации
Ассура − Артоболевского относят ко второму классу.
а
б
в
г
д
Рис. 16
Следующая группа, удовлетворяющая условию (2.3), представляет собой
сложную кинематическую цепь, состоит из четырех звеньев и шести
кинематических пар (рис. 17, а) и относится к третьему классу.
а
б
Рис. 17
Структурные группы делятся на классы в зависимости от класса контура.
Контур − замкнутая область части плоскости, занятая звеном или ограниченная
со всех сторон звеньями. Класс контура определяют количеством
кинематических пар, входящих в этот контур. На рис. 17, а изображена группа,
пары которой образуют четыре контура: АВ, СЕ, DF − второго класса и BCD −
третьего. На рис. 17, б показана сложная кинематическая цепь, пары которой
образуют три контура: АВС и DEF − третьего класса и BCFD − четвертого
класса. Следовательно, это группа четвертого класса.
Наиболее распространенными являются группы второго класса, которые
в зависимости от количества и расположения вращательных и поступательных
пар разделяются на пять видов (см. рис. 16):
а − первый, б − второй, в − третий, г − четвертый и д − пятый.
Для определения класса механизма из его состава выделяют группы
в порядке, обратному тому, в котором они присоединялись к простейшему
механизму, т. е. начиная с наиболее удаленной от ведущего звена части
механизма. Группы выделяются попытками при одновременной проверке
степени подвижности оставшейся части механизма, которая должна сохранять
возможность работы. Процесс выделения структурных групп называют
структурным анализом, который рекомендуется выполнять в такой
последовательности:
на кинематической схеме обозначают кинематические звенья и пары;
определяют количество подвижных звеньев и кинематических пар
четвертого и пятого классов и подсчитывают степень подвижности;
при наличии пассивных звеньев и подвижностей исключают их и вновь
подсчитывают степень подвижности;
заменяют высшие кинематические пары цепями с низшими парами и
проверяют степень подвижности;
выделяют структурные группы и устанавливают их класс и вид,
определяя степень подвижности оставшейся части механизма.
Пример. Выполнить структурный анализ перфорирующего механизма
УПД ЕС−9020 (рис. 18).
Эксцентрик 1, жестко сидящий на главном валу перфоратора, посред-
ством щетки 2 сообщает движение оси В, на которой расположены толкатели
пуансонов 4. Если кодовый электромагнит ЭМ возбужден, то его якорь 7,
притягиваясь, разворачивает угловой рычаг 6 по часовой стрелке, и толкатель 4
под действием пружины 9 поворачивается по часовой стрелке и при своем
движении вверх проходит мимо торца пуансона 5. Пробивка отверстия
отсутствует. При обесточивании ЭМ якорь 7 под действием пружины 8
разворачивает угловой рычаг 6 против часовой стрелки. Толкатель 4 при этом
разворачивается против часовой стрелки и при своем движении вверх
воздействует
в точке D на пуансон 5, который пробивает отверстие в
носителе информации (НИ). Пуансон возвращается в текущее положение рамкой
10, которая в точке В шарнирно соединена со звеньями 2 и 3.
Структурный анализ выполним при обесточенном ЭМ. В этом случае
угловой рычаг 6 превращается в стойку, по которой скользит горизонтальный
конец толкателя 4, с которым совместно движется рамка 10.
Рис. 18
Механизм при этом состоит из пяти подвижных звеньев (n = 5), имеет две
высших (P4 = 2) и шесть низших (P5 = 6) кинематических пар. Степень
подвижности по (2.2)
W = 3n − 2P5 − P4 = 3⋅5 − 2⋅6 − 2 = l.
В составе механизма отсутствуют пассивные звенья и пассивности.
Заменяем высшие пары четвертого класса С и D цепями с низшими парами
пятого класса. Заменяющий механизм (рис. 19, а) состоит из семи подвижных
звеньев (n = 7) и десяти кинематических пар пятого класса (Р5 =10). Степень
подвижности заменяющего механизма W =3n − 2Р5 = 3⋅7 − 2⋅10 = 1
соответствует подвижности действительного.
б
г
а
в
д
Рис. 19
Выделенные группы показаны на рис. 19, б: первая − звенья 5, 6 и
кинематические пары Е, D2, D1 − второго класса пятого вида; вторая − звенья 7,
4 и кинематические пары С1, С2, В2 − второго класса второго вида; третья −
звенья 3, 2 и пары О3, В1, А − второго класса первого вида; простейший
механизм − звенья 0, 1 и кинематическая пара О1 − первого класса. Класс
механизма − второй.
Вопросы для самопроверки
1. Какие тела называют свободными? Что понимают под связью?
2. Что называют кинематической парой; элементом кинематической
пары? По каким признакам классифицируются кинематические пары?
Приведите примеры кинематических пар различных классов.
3. Что называют кинематической цепью? Какие виды кинематических
цепей используются для образования механизмов? Сформулируйте основной
принцип образования сложных механизмов по Ассуру − Артоболевскому.
4. Какие связи и подвижности называют пассивными? Приведите
примеры механизмов с пассивными связями и пассивными подвижностями.
5. Как выполняют замену высших кинематических пар цепями с низшими
парами? Приведите примеры замены высших кинематических пар цепями с
низшими парами.
6. Какая кинематическая цепь называется структурной группой?
Изобразите кинематические схемы простейших механизмов первого класса,
используемые в периферийных устройствах ЭВМ.
7. Какова последовательность выполнения структурного анализа
механизмов? Изобразите кинематические схемы структурных групп второго
класса?
8. Сформулируйте принцип структурной и кинематической
эквивалентности, используемый при замене высших кинематических пар
цепями с низшими парами.
9. Как определить класс структурной группы; класс механизма?