связи и реакции связей - Томский Государственный

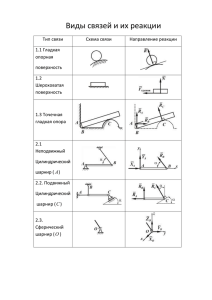
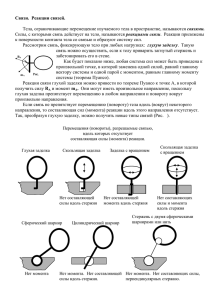
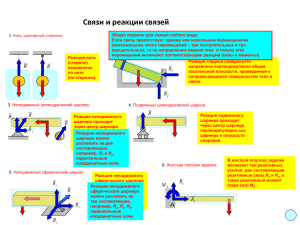
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Томский государственный архитектурно-строительный университет»
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
Методические указания
к самостоятельному изучению темы
Составители В.Г. Симоненко, О.Н. Лысак
Томск 2012
Теоретическая механика. Связи и реакции связей: методические указания к самостоятельному изучению темы / Сост.
В.Г. Симоненко, О.Н. Лысак. – Томск: Изд-во Том. гос. архит.строит. ун-та, 2012. – 33 с.
Рецензент ст. препод. М.В. Геттингер
Редактор Е.Ю. Глотова
Методические указания предназначены для самостоятельного
изучения темы «Связи и реакции связей» и соответствуют государственному образовательному стандарту подготовки бакалавров и специалистов по дисциплине «Теоретическая механика» всех направлений всех форм обучения.
Печатаются по решению методического семинара кафедры теоретической механики, протокол № 3 от 3 октября 2011 г.
Утверждены и введены в действие проректором по учебной работе В.В. Дзюбо
с 01.11.2012
по 01.11.2017
Оригинал-макет подготовлен авторами
Подписано в печать 30.11.12.
Формат 60×84. Бумага офсет. Гарнитура Таймс.
Уч.-изд. л. 1,7. Тираж 140 экз. Заказ № 555.
Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная, 2.
Отпечатано с оригинал-макета в ООП ТГАСУ.
634003, г. Томск, ул. Партизанская, 15.
2
ОГЛАВЛЕНИЕ
Введение................................................................................4
1. Связи и реакции связей ..................................................4
1.1. Связи, используемые в плоских
конструкциях задач статики........................................9
1.1.1. Гладкая поверхность, опорное ребро ...................9
1.1.2. Ползун с шарниром .............................................10
1.1.3. Неподвижный цилиндрический шарнир
или подшипник..................................................11
1.1.4. Подвижный цилиндрический шарнир
(или опора на катках) ........................................14
1.1.5. Гибкая связь.........................................................16
1.1.6. Невесомый шарнирный стержень.......................17
1.1.7. Жёсткая заделка ..................................................19
1.1.8. Скользящая заделка.............................................20
1.1.9. Бискользящая заделка .........................................21
1.1.10. Шероховатая поверхность ................................21
1.2. Связи, используемые в пространственных
конструкциях задач статики .........................................22
1.2.1. Шаровой шарнир. Подпятник.............................22
1.2.2. Подшипник, петля (цилиндрический шарнир) ..24
1.2.3. Жёсткая заделка ..................................................25
2. Порядок (план) решения задач ....................................26
Список рекомендуемой литературы ...............................29
Приложение. Типы связей .................................................30
3
Образование – это то, что остаётся, когда мы уже забыли всё, чему
нас учили.
Д. Галифакс (XVIII в.)
ВВЕДЕНИЕ
Большинство законов классической механики выведены
для свободных материальных объектов, в число которых входят материальные точки, механические системы и твёрдые тела. Как правило, все эти объекты на практике являются несвободными. В связи с этим возникает проблема выявления связей, ограничивающих движение объектов и правильного освобождения от них.
Представленные методические указания дают возможность
дополнительно проработать данную тему и получить знания, позволяющие приобрести необходимые умения и навыки для успешного решения поставленных задач.
В результате изучения темы «Связи и реакции связей» студент должен обладать стремлением к саморазвитию, повышением своей квалификации и мастерства (ОК-6), для этого
необходимо:
1) творчески подойти к изучению представленного теоретического материала, дополняя в случае необходимости проработку рекомендуемой литературы для дальнейшего успешного
решения задач как теоретической механики, так и задач сопротивления материалов. Для этого требуется качественно разобрать
понятие связей, научиться правильно их классифицировать;
2) уметь правильно освобождаться от выявленных связей,
заменяя их реакциями, приложенными к данному телу (механизму);
3) владеть полученными знаниями при решении практических задач, получая при этом необходимые навыки.
4
1. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
Свободным материальным объектом называется такой
объект, который не скреплён с другими материальными объектами и которому из данного положения можно сообщить любое
перемещение в пространстве под действием приложенной к нему системы сил или, другими словами, объект, не имеющий никаких закреплений, препятствующих его движению.
Под материальными объектами будем понимать материальную точку, механическую систему и её частный случай – абсолютно твёрдое тело (твёрдое тело).
При решении большинства задач механики приходится иметь
дело с телами несвободными, т. е. с такими, которые соприкасаются
или скреплены с другими телами, благодаря чему становятся невозможными те или иные перемещения данного тела. Если тело несвободно, то говорят, что на него наложены связи.
Любое тело, ограничивающее свободу перемещения данного объекта, называется связью, наложенной на этот объект.
Иначе это понятие можно выразить так: связью называется любая конструкция, уменьшающая количество степеней свободы
данного материального объекта.
Количеством степеней свободы материального объекта
называется число независимых параметров, с помощью которых
можно определить (задать) его положение на плоскости или в
пространстве. Каждая связь имеет свою кинематическую характеристику, которая показывает, каким движениям материального объекта она препятствует и сколько степеней свободы она
уничтожает (отнимает).
Так, пространственное свободное твёрдое тело, изображённое на рис. 1, а, может совершать независимые поступательные движения вдоль трёх осей декартовой системы координат и
три вращательные движения вокруг тех же осей. Следовательно,
5
пространственное свободное твёрдое тело имеет шесть степеней
свободы. Плоское твёрдое тело, показанное на рис. 1, б, может
совершать на плоскости два независимых поступательных перемещения (вдоль осей x и y) и одно вращательное движение вокруг какого-либо центра вращения (точки), называемого полюсом. Отсюда, плоское свободное твёрдое тело на плоскости имеет три степени свободы.
z
а
б
y
О
О
y
x
x
в
г
z
y
xM
M
M
yM
zM
O
xM
x
O
y
yM
Рис. 1
6
x
Положение любой свободной точки М в пространстве
(рис. 1, в) может быть определено тремя координатами xM , yM ,
zM , т. е. она имеет три степени свободы, а на плоскости
(рис. 1, г) – двумя координатами xM , yM и соответственно имеет две степени свободы.
Для дальнейшего понимания излагаемого материала
вспомним аксиому сил действия и противодействия. Рассмотрим
важный случай взаимодействия двух материальных объектов
(точек, тел) А и В. Пусть, например, точка А действует на точку
В с силой FA . Назовём эту силу силой действия. Точка В будет
обязательно противодействовать на точку А с силой FB . Эту силу назовём силой противодействия.
FB
FA
А
В
Аксиома утверждает: всякой силе действия есть равная по
модулю, но противоположно направленная вдоль прямой, соединяющей эти точки, сила противодействия.
Современная трактовка аксиомы такова:
силы, с которыми действуют друг на друга две точки
(тела), всегда равны по модулю и противоположно направлены
вдоль прямой, соединяющей эти точки, т. е.
FВ   FА .
Согласно этой аксиоме между данным телом и связью
(опорой) существует механическое взаимодействие. Воздействие тела на связь называется силой действия, которая всегда
приложена к связи. Воздействие же связи на тело – силой противодействия.
Сила противодействия связи, приложенная к рассматриваемому телу, называется реакцией связи.
7
Силы действия и противодействия не образуют уравновешенную систему сил, так как они приложены к разным телам:
силы действия приложены к связи, силы противодействия – к
данному телу (объекту).
Основные законы классической механики записаны для
свободных материальных объектов. Условия равновесия для
различных конструкций также получены исходя из того, что они
должны быть свободными, т. е. освобождёнными от связей.
В связи с этим возникла необходимость сформулировать
принцип (аксиому) освобождения от связей:
любое несвободное тело можно условно представить
свободным, если мысленно освободить его от связей, заменив
действие этих связей соответствующими реакциями, приложенными к рассматриваемому телу.
Пользуясь этим принципом, к несвободному телу можно
применять условия равновесия, выведенные в статике для свободного тела. Нужно только в число сил, действующих на тело, обязательно включать и силы реакций связей.
Большинство задач статики как раз и заключается в определении сил реакций связей. При знании их будут известны и силы
давления на связи, т. е. будут известны данные, необходимые для
расчёта на прочность самих конструкций.
В механических системах, образованных путём сочленения
нескольких твёрдых тел, наряду с внешними связями (опорами)
имеются внутренние связи между взаимодействующими телами.
Внутренней связью называется такая связь, которая не препятствует перемещению всей системы в целом, а налагает ограничения только на относительное расположение точек (тел) системы.
Опорными называются связи, осуществляющие прикрепление конструкции к некоторому основанию (например, к земле).
Так как прикрепление может быть осуществлено различными способами, необходимо научиться правильно классифи8
цировать наложенные на материальный объект связи и правильно от них освобождаться.
Значение реакции связи зависит от других действующих
сил, и наперёд неизвестно (если никакие другие силы на тело не
действуют, реакции равны нулю); для её определения надо решить соответствующую задачу механики. В общем случае реакция связи направлена в сторону, противоположную той, куда
связь не даёт перемещаться телу. Когда связь может препятствовать перемещениям тела по нескольким направлениям, направление реакции такой связи тоже наперёд неизвестно и должно
определяться в результате решения задачи.
Правильное определение направлений реакций связей при
решении задач механики играет очень важную роль.
Рассмотрим, как классифицируются различные типы связей и как правильно освободиться от них.
1.1. СВЯЗИ, ИСПОЛЬЗУЕМЫЕ
В ПЛОСКИХ КОНСТРУКЦИЯХ ЗАДАЧ СТАТИКИ
1.1.1. Гладкая опорная поверхность, опорное ребро
Гладкой называется поверхность, трением тела о которую
можно пренебречь (связи без трения относятся к так называемым идеальным связям, рассмотрением таких связей мы пока и
ограничимся).
Так как гладкая опорная поверхность не препятствует
скольжению по ней поверхности тела, то реакция N гладкой поверхности (рис. 2) направлена всегда по нормали к поверхности
тела и поверхности связи в их точке касания. Нормалью к поверхности называется перпендикуляр к касательной плоскости,
проведённый через точку касания.
9
N
N
Рис. 2
Если одна из соприкасающихся поверхностей имеет заострение (уступ, угол) (рис. 3), то реакция должна быть направлена
по нормали к другой гладкой поверхности (такой вид связи иногда называют опорное ребро). Например, к гладкому брусу АВ
(рис. 3, а), опирающемуся в точке А на пол и в точке В на ребро
стены, приложены реакции RA пола и RB ребра, направленные
так, как изображено на рисунке.
в
б
а
RC
RB
С
В
С
RB
RA
А
А
В
В
А
RC
г
С
RB
А
RA
В
Рис. 3
10
RA
Рассуждая аналогично, реакции бруса (рис. 3, б, г) будут
направлены так, как изображено на рис. 3, в, г.
1.1.2. Ползун с шарниром
В этом типе связи (рис. 4) из трёх степеней свободы остаются две, третья же в связи с запретом движения по нормали к
направляющим отсутствует, т. е. в этом случае присутствует
только одна реакция N A , направленная перпендикулярно направляющим.
NA
А
А
Рис. 4
1.1.3. Неподвижный цилиндрический шарнир
или подшипник
Цилиндрическим шарниром (рис. 5, а) называется соединение двух тел посредством пальца (болта), проходящего через
отверстия в этих телах. Диаметр отверстия во втулке (рис. 5, б)
несколько больше диаметра пальца. Тело, жёстко скреплённое с
втулкой, может только вращаться вокруг оси шарнира (оси
пальца), перпендикулярной к плоскости рисунка, не имея возможности перемещаться по этой плоскости, т. е. в этом виде связи остаётся только одна степень свободы – вращение.
11
а
б
г
в
втулка
R
YA
RА
φ
А
А
палец
А
XA
Рис. 5
Во многих случаях можно пренебречь трением в шарнире
(между поверхностями пальца и втулки). В таком шарнире (называемом «идеальным») нет препятствий ни для поворота втулки вокруг оси пальца, ни для её перемещения вдоль этой оси.
Идеальный шарнир препятствует лишь перемещению втулки в
направлении нормали к поверхности втулки и пальца, и, следовательно, его реакция может быть направленной только по этой
нормали (по радиусу пальца). Но так как втулка в зависимости
от её расположения и приложенных к ней сил может прижиматься к любой точке пальца, то указать заранее направление
реакции цилиндрического шарнира нельзя. Единственное, что
можно утверждать (если пренебречь трением в шарнире), это
то, что реакция неподвижного цилиндрического шарнира лежит в плоскости, перпендикулярной к его оси, и имеет радиальное направление.
Для определения реакции связи в тех случаях, когда её направление оказывается неопределённым, полезно заменить искомую реакцию несколькими составляющими, представляющими собой векторные проекции этой реакции на оси выбранной
декартовой системы координат, неизвестными теперь только по
величине. Например, реакции шарнира А (рис. 5, а) или упора А
(рис. 6, а) удобно разложить на горизонтальную X A и вертикальную YA составляющие, если оси декартовой системы координат направлены стандартно (рис. 5, г, рис. 6, б). В дисциплине
12
«Сопротивление материалов» горизонтальную составляющую
обозначают H A , а вертикальную – VA .
а
б
YA
XA
А
А
Рис. 6
В обоих случаях можно считать, что связь А (шарнир или
упор) препятствует перемещению тела как в горизонтальном,
так и в вертикальном направлениях.
В общем же случае, формально
y
считая, что реально существующая
x реакция шарнира имеет проекции на
оси выбранной для данной задачи деYA
картовой системы координат, соответX
А
A
ствующие векторные составляющие
реакции направляют вдоль этих осей
Рис. 7
(рис. 7).
После того как будут найдены модули каждой из составляющих реакций, можно найти (при необходимости) и полную
реакцию RA связи как равнодействующую её векторных составляющих. Для этого надо скалярные проекции X A , YA сделать
векторными X A  X Ai , YA  YA j , и тогда реакция RA будет направлена по диагонали параллелограмма со сторонами X A , YA ,
отложенными в выбранном масштабе.
Заметим, что, раскладывая реакцию на составляющие,
можно не заботиться о правильности выбора направлений по
намеченным линиям их действия. В случае, если в действитель13
ности та или иная составляющая окажется направленной в сторону, противоположную предложенной, мы будем получать для
неё в ответе отрицательное значение.
Шарнирно-неподвижная опора схематически изображается
двумя стержнями (рис. 8, а и б), соединёнными между собой на
одном конце общим шарниром А, ось которого, очевидно, будет
неподвижной. Реакция такой опоры проходит через ось шарнира,
но не известна ни по модулю, ни по направлению и, следовательно, характеризуется двумя неизвестными элементами.
в
б
а
А
А
А
Рис. 8
Определение модуля и направления реакции шарнирнонеподвижной опоры можно, как было сказано выше, заменить
определением модулей двух составляющих этой реакции. Наличие в схеме шарнирно-неподвижной опоры двух стержней указывает на то, что неизвестны две составляющие реакции данной
связи.
Шарнирно-неподвижная опора для балки или стержня изображается так, как показано на рис. 8, в.
Кроме неподвижного опорного цилиндрического шарнира
в составных конструкциях встречаются соединительные шарниры (рис. 9, а), скрепляющие два соседних звена (внутренняя
связь).
б
а
YC
С
XC
X C С
С
YC
Рис. 9
14
Для того чтобы определить реакции в таком шарнире, необходимо расчленить конструкцию по этому шарниру. Тогда, с
учётом аксиомы сил действия и противодействия, реакции в каждой части расчленённой конструкции в шарнире С при стандартном расположении осей декартовой системы координат будут иметь вид (рис. 9, б), при этом X C  X C и YC  YC .
1.1.4. Подвижный цилиндрический шарнир
(или опора на катках)
Подвижная шарнирная опора представляет собой сочетание цилиндрического шарнира и гладкой поверхности, вдоль
которой опора может перемещаться на катках. Это обстоятельство и обусловливает направление реакции R .
Мы говорили до сих пор о связях, осуществляемых абсолютно гладкими поверхностями. Эти связи препятствуют перемещению тел только в направлении, нормальном к поверхности,
и характеризуются одной нормальной реакцией. Негладкая поверхность не только препятствует перемещению, нарушающему
связь, но и затрудняет перемещение по самой поверхности. Следовательно, реакция негладкой поверхности имеет две составляющие: одну – нормальную к поверхности, и другую – лежащую в плоскости скольжения (в общей касательной плоскости к
поверхности тела и опорной поверхности) и направленную в
сторону, противоположную той, в которую двигают или пытаются сдвинуть тело. Первая составляющая является нормальной
реакцией, вторая носит название силы трения. Следовательно,
негладкие опорные поверхности отличаются тем, что для них
приходится дополнительно учитывать силу трения.
О том, как это делается, мы будем говорить дальше, в
п. 1.1.7. Сейчас отметим только, что хотя идеально гладких поверхностей, а следовательно, и идеальных связей в действительности не существует, но на практике во многих случаях силой
15
трения можно пренебречь и практически считать связи идеальными.
Подвижность катка настолько велика, и, следовательно,
сила трения настолько мала, что можно считать такую связь препятствующей лишь перемещению, перпендикулярному к опорной плоскости, почему она и характеризуется всегда одной
нормальной реакцией R (рис. 10; 11, а).
R
Рис. 10
Таким образом, такой тип связи допускает движение тела
параллельно опорной плоскости и возможность вращения вокруг оси шарнира, перпендикулярной плоскости, в которой лежит механизм, т. е. из трёх возможных степеней свободы одна
отнимается, та, которая соответствует движению по нормали к
опорной плоскости.
а
R
б
в
Рис. 11
Такая опора представляет собой так называемую шарнирно-подвижную опору и часто схематически изображается одним
стержнем, перпендикулярным поверхности с шарнирами на кон16
цах (рис. 11, б). Реакция подобной опоры проходит через ось
шарнира и направлена по нормали к опорной поверхности. Наличие в схеме опоры одного стержня указывает на то, что неизвестен лишь один элемент реакции шарнирно-подвижной опоры –
её модуль.
Шарнирно-подвижная опора для стержня может изображаться так, как показано на рис. 11, в.
1.1.5. Гибкая связь (нить, трос, цепь)
Пусть груз весом G подвешен в точке А на нитях так, как
показано на рис. 12, а.
б
а
В
С
ТС
ТВ
А
А
G
G
Рис. 12
Если считать нити нерастяжимыми, то они не дают точке А
удаляться от точки С по направлению нити СА и от точки В по
направлению ВА. Следовательно, реакции Т С и Т В нерастяжимых гибких нитей всегда направлены вдоль нитей к точке их
подвеса (реакцию гибкой связи часто обозначают буквой Т).
Другими словами, направление реакции в гибкой связи известно заранее и точно – она всегда направлена по нити от точки
тела, к которому она прикреплена, вдоль нити так, как показано
на рис. 13, в сторону, противоположную движению точки (тела),
если связь рассечь.
17
ТВ
ТА
А
В
А
T
В
G
Рис. 13
1.1.6. Невесомый шарнирный стержень
Нити на рис. 13 могут быть без изменения направлений реакций заменены твёрдыми стержнями, если пренебречь их весом
и считать стержни соединёнными посредством идеальных шарниров. Учитывая, что шарниры идеальные, стержни абсолютно
твёрдые, невесомые (как правило, их весом можно пренебречь)
и все силы приложены к шарнирам, стержни будут подвержены
только или сжимающим, или растягивающим усилиям. Эти силы могут только растягивать или сжимать стержни. В самом деле, как мы знаем, идеальный шарнир характеризуется только
одной, нормальной к оси шарнира реакцией. Но две силы, приложенные к стержню в его концах, могут уравновешиваться
только тогда, когда они равны по модулю и направлены по одной прямой в противоположные стороны. Следовательно, реакция невесомого и шарнирно закреплённого стержня направлена вдоль линии, соединяющей центры шарниров.
Подобным же образом, очевидно, направлены и реакции
шарнирно закреплённых стержней, подпирающих тело (рис. 14).
Алгебраическое значение силы, действующей вдоль стержня и
растягивающей или сжимающей его, называется усилием в
стержне; при растяжении усилие обычно считается положительным, его направляют от узла, а при сжатии – отрицательным
(направлено в узел). Реакции стержней часто обозначают буквами S или N.
18
NC
С
А
А
В
С
NB
В
NA
SB
SC
С
В
G
D
А
Рис. 14
1.1.7. Жёсткая заделка (защемление)
Жёсткая заделка (рис. 15, а) представляет собой такое внедрение данного тела в другое, при котором нет взаимных перемещений этих тел (например, гвоздь вбит в стену, балконная
плита заделана в стену, столб врыт в землю). Реакция заделки
представляет собой силы, распределённые по поверхности контакта тел. Если на рассматриваемое тело действует плоская система сил, то реакцию жёсткой заделки представляют в виде двух
составляющих X A , YA и пары сил с алгебраическим моментом
M A (рис. 15, б, в).
Число степеней свободы для данного тела в случае жёсткой заделки равно нулю.
19
б
а
YA
А
А
МA
F1
F2
XA
Fn
y
в
YA
А
XA
МA
x
Рис.15
Жёсткая заделка часто схематически изображается так, как
показано на рис. 16.
Рис. 16
1.1.8. Скользящая заделка
Скользящая заделка является частным случаем жёсткой, но
в отличие от последней появляется одна степень свободы, позволяющая перемещаться данному телу вдоль направляющих
(рис. 17, а). Реакция скользящей заделки состоит из силы, перпендикулярной направляющим ( YA , YB – рис. 17, б, в и X B –
20
рис. 17, г) и пары сил с алгебраическим моментом М A (рис. 17, б)
или М В (рис. 17, в, г).
а
г
в
б
YВ
YA
А
А
MB
В
МA
MB
XB
В
Рис. 17
Скользящая заделка схематически изображается так, как
показано на рис. 18.
Рис. 18
1.1.9. Бискользящая заделка
Бискользящая заделка представляет собой такую связь, которая препятствует телам взаимно поворачиваться, при этом сохраняется возможность любого движения в плоскости этой заделки, и, следовательно, эта связь осуществляет две степени
свободы тела. Пример такой связи – крестовина (рис. 19, а). Реакция бискользящей заделки сводится к паре сил с алгебраическим моментом М A (рис. 19, б, г).
Схематически бискользящая заделка изображается так, как
показано на рис. 19, в.
21
б
а
А
г
в
А
А
А
МA
МА
Рис. 19
1.1.7. Шероховатая поверхность
Шероховатость поверхности специально оговаривается в
условии задачи.
Реакция такой связи заранее не известна по направлению,
поэтому её раскладывают на две составляющие: нормальную N
и касательную (силу трения скольжения Fтр ) (рис. 20), т. е.
R  N  Fтр . Модули N и Fтр определяются из соответствующих условий равновесия. Сила трения скольжения направляется
в сторону, противоположную возможному перемещению тела по
поверхности.
N
Fтр
Рис. 20
Величина силы трения определяется по формуле
0  Fтр  Fтрmax , где Fтрmax  f N .
22
Величина f (коэффициента трения) либо задается в задаче, либо
является искомой величиной.
1.2. СВЯЗИ, ИСПОЛЬЗУЕМЫЕ
В ПРОСТРАНСТВЕННЫХ КОНСТРУКЦИЯХ
ЗАДАЧ СТАТИКИ
1.2.1. Сферический (шаровой) шарнир. Подпятник
Сферический шарнир позволяет соединяемым телам совершать пространственные взаимные вращения вокруг центра
шарнира. Реакция такого шарнира проходит через его центр и
может иметь любое направление в пространстве. При решении
задач реакцию сферического шарнира представляют в виде трёх
составляющих, направленных вдоль координатных осей декартовой системы координат (рис. 21).
При этом типе связи тело обладает тремя степенями свободы – возможностью вращения вокруг трёх осей x, y, z, при запрете перемещения центра шарнира.
z
z
ZA
А
А
y
x
x
y
YA
XA
Рис. 21
23
Подпятник (рис. 22, а, б) представляет собой соединение
цилиндрического шарнира с опорной плоскостью. Такая связь
позволяет вращаться валу (цилиндру) вокруг его оси и перемещаться вдоль неё, но только в одном направлении.
б
а
в
z
z
ZB
В
y
В
x
x
y
В
XB
YB
Рис. 22
Реакция подпятника (рис. 22, в) складывается из реакции
цилиндрического подшипника, лежащей в плоскости, перпендикулярной к его оси (в общем случае она может быть разложена
на составляющие X B , YB ) и нормальной реакции Z B опорной
плоскости.
Аналогичным способом направляются и реакции упорного
подшипника А (рис. 23); однако следует иметь в виду, что составляющая YA , действующая вдоль оси упорного подшипника,
может быть направлена только к телу.
z
ZA
YA
x
А
В
y
XA
Рис. 23
24
А
ZB
В
XB
1.2.2. Подшипник, петля (цилиндрический шарнир)
а
б
ZB
z
z
y
В
ZA
XB
ZB
A
XA
B
y
XB
ZA
А
XA
x
x
C
SC
Рис. 24
На рис. 24, а в точках А и В представлен тип связи, называемый подшипником. Очень часто его используют с целью
максимального уменьшения сил трения между звеньями механизма, например, подшипники устанавливают на концах вращающегося вала.
На рис. 24, б в точках А и В изображён тип связи, который
называется цилиндрическим шарниром, или, в обиходе, петлёй.
Его применяют в тех случаях, когда два соседних звена должны
вращаться относительно друг друга вокруг общей оси вращения.
Эти пространственные типы связей аналогичны плоскому
цилиндрическому шарниру и, следовательно, все выводы, полученные для цилиндрического шарнира, справедливы и для подшипника, и для петли. Т. е., реакции в точках А и В состоят из
двух составляющих X A , Z A и X B , Z B . Вдоль оси y составляющей силы реакции не возникает, подшипник (петля) не препятствует движению тела в этом направлении.
25
1.2.3. Жёсткая заделка
Если же на рассматриваемое тело действует пространственная система сил, то реакцию жёсткой заделки представляют в
виде трёх составляющих X A , YA , Z A и трёх компонентов момента М Ax , М Ay , М Az .
z
М Az
ZA А
А
XA
YA М Ay
М Ax
y
x
Рис. 25
Подводя итог анализу различных видов связей приведём
таблицу (см. приложение), в которой для различных видов связей (или точнее, способов соединения тел между собой) показаны соответствующие реакции.
2. ПОРЯДОК (ПЛАН) РЕШЕНИЯ ЗАДАЧ
Приступая к решению задачи, необходимо разобраться в
условии задачи и рисунке, а затем:
1) составить расчётную схему;
2) определить вид полученной системы сил и выбрать соответствующие ей уравнения равновесия;
3) выяснить, является ли задача статически определимой
(т. е. не превышает ли число неизвестных числа уравнений);
26
4) составить уравнения равновесия и определить из них
искомые реакции связей;
5) сделать проверку полученных результатов.
Остановимся поподробнее на составлении расчётной схемы.
2.1. Расчётная схема
Расчётная схема – это чертёж, который включает:
– объект равновесия (точку, тело или систему тел);
– активные (заданные) силы, пары сил; распределённые
нагрузки следует заменить эквивалентными им по действию сосредоточенными силами;
– силы реакции, заменяющие действия отброшенных связей;
– все необходимые размеры.
Этот чертеж и схема могут либо помогать решать задачу,
либо, при небрежном отношении к чертежу, просто провоцировать на ошибки.
Чтобы Ваши чертежи помогали решать задачи, необходимо знать следующее:
а) никогда не следует экономить время на оформлении
чертежа (расчетной схемы) к решаемой задаче. Чем яснее чертеж, тем Вы быстрее решите задачу и с меньшей вероятностью
ошибки;
б) чертеж к задаче должен быть достаточно крупным, чтобы легко читались все заданные размеры, хорошо были видны
углы, образуемые векторами сил или линиями чертежа с осями
координат;
в) тело, равновесие которого рассматривают, должно быть
хорошо видно, для чего оно рисуется более толстыми линиями;
все векторы сил, стрелки моментов пар сил должны четко выделяться на фоне чертежа. «Плохо» выделенный вектор легко пропустить при составлении уравнений равновесия. Это влечет за
собой и неверное решение задачи, и потерю времени на поиск
ошибки;
27
г) важно, чтобы зрительная пропорциональность размеров
на чертеже соответствовала заданной в условии задачи.
Еще более важно, чтобы углы, которые образуют силы
или линии чертежа с теми или иными осями координат, соответствовали заданным.
Углы в 30º, 45º, 60º и 90º желательно научиться рисовать
достаточно точно от руки.
Замечания
1. При выполнении расчётной схемы изображение тела без
связей не является строго обязательным; иногда воздействие реакций связей на тело показывают на исходном чертеже конструкции, подразумевая, что это тело «свободное».
2. При замене связей (опор) силами реакций помнить:
– если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление её реакции противоположно этому направлению;
– если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают её
составляющими X , Y , показывая их параллельно выбранным
осям координат x и y (направление составляющих реакций связей на чертеже следует изображать независимо от направлений
и величин действующих активных сил). Числовые значения реакций будут определяться последующим расчётом; если алгебраическое значение реакции получено со знаком минус, то значит соответствующая реакция имеет направление, противоположное первоначально принятому.
3. Решение уравнений равновесия будет тем проще, чем
меньшее число неизвестных будет входить в каждое из них. Поэтому при составлении уравнений равновесия следует:
– координатные оси x и y располагать так, чтобы одна из
осей была перпендикулярна к линии действия хотя бы одной из
неизвестных сил, в этом случае эта неизвестная сила исключается из соответствующего уравнения равновесия;
28
– за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных реакций связей, тогда моменты этих сил не войдут в уравнение
моментов.
4. Если сила F в плоскости xy имеет две составляющие её
силы Fx и Fy , то при вычислении момента силы F вокруг некоторой точки О полезно применить теорему Вариньона, вычислив сумму моментов составляющих её сил относительно этой
точки.
5. Если к телу в числе других сил приложена пара сил, то
её действие учитывается только в уравнении моментов сил, куда
вносится момент этой пары с соответствующим знаком.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Бабанов, В.В. Теоретическая механика для архитекторов. В
2 т. Т. 1: учебник / В.В. Бабанов. – М.: Академия, 2008. – 256 с.
Богомаз, И.В. Теоретическая механика: учебное пособие
для вузов в 2 т. Т. 1 / И.В. Богомаз. – М.: Изд-во АСВ, 2005. –
191 с.
Бутенин, Н.В. Курс теоретической механики. В двух томах / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. – СПб.: Лань, 2009.
– 736 с.
Никитин, Н.Н. Курс теоретической механики: учебник /
Н.Н. Никитин. – СПб.: Лань, 2010. – 720 с.
Тарг, С.М. Краткий курс теоретической механики: учебник
/ С.М. Тарг. – М.: Высшая школа, 2006. – 416 с.
Яблонский, А.А. Курс теоретической механики: учебник /
А.А. Яблонский, В.М. Никифорова. – СПб.: Лань, 2008. – 768 с.
29
ПРИЛОЖЕНИЕ
ТИПЫ СВЯЗЕЙ
Название связей
и их обозначение на схемах
Гладкая поверхность
Реакции связей
N
N
Реакция N направлена к телу. Реакция гладкой поверхности направлена
по общей нормали к поверхностям
соприкасающихся тел
Ползун с шарниром
NA
А
А
Реакция направлена перпендикулярно направляющим
Опорное ребро
RC
С
С
А RB
RA
А
В
В
30
Реакция такой связи направлена по
нормали к той поверхности, которая
не имеет ребра
Название связей
и их обозначение на схемах
Реакции связей
Гибкая связь
Q
Т
Q
Р
Q
Реакция направлена вдоль нити от
тела (нить работает только на растяжение), Р – вес лампы
Невесомый стержень с шарнирами на концах
А
С
А
В
SC
SB
С
В
SA
Реакция S направлена вдоль прямой,
проходящей через шарниры, стержень работает либо на растяжение,
либо на сжатие
Подвижный цилиндрический
шарнир (каток)
R
R
Реакция направлена перпендикулярно опорной плоскости
31
Название связей
и их обозначение на схемах
Неподвижный цилиндрический шарнир
Реакции связей
YA
А
А
XA
А – ось подшипника перпендикулярна чертежу
Угол в угле
RB
В
В
YA
XA
А
А
Жёсткая заделка
А
YA
А
МA
Скользящая заделка
XA
YA
А
mA
32
Название связей
и их обозначение на схемах
Бискользящая заделка
Реакции связей
М
Шаровой шарнир, подпятник
ZA
z
А
XA
А
z
А
y
x
В
x
XB
y
Петля, подшипник
z
ZA
z
A
B
y
ZB
YA
YB
В
ZB
A
XB
XA
B
y
x
x
Ось подшипника В совпадает с
осью y
Составляющие реакции лежат в
плоскости, перпендикулярной оси
подшипника
Жёсткая заделка
z
М Az
ZA А
А
XA
y
YA М Ay
М Ax
x
33