Заряженная капля
реклама

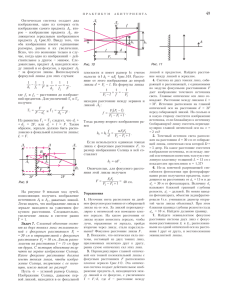
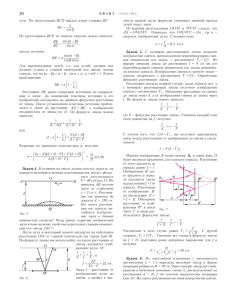
a F F á F F Ðèñ. 4 ñ èçâåñòíûì ðàäèóñîì êðèâèçíû R. Íà ðèñóíêå 5 ïîêàçàíî öåíòðàëüíîå ñå÷åíèå ëèíçû, CC′ åå îñü, Î öåíòð êðèâèçíû ëèíçû â îáëàñòè âåðøèíû. Ïóñòü n ïîêàçàòåëü ïðåëîìëåíèÿ ìàòåðèàëà ëèíçû, äëÿ îðãñòåêëà n = 1,47 (äëÿ äëèí âîëí ñâåòà 0,5 0,6 ìêì), à n0 ¾1 ïîêàçàòåëü ïðåëîìëåíèÿ âîçäóõà. Âäîëü îñè íà ëèíçó ïàäàåò ïàðàëëåëüíûé ïó÷îê ñâåòà. Ðàññìîòðèì õîä îäíîãî èç ëó÷åé, ïàäàþùèõ íà ëèíçó â ïðîèçâîëüíóþ òî÷êó Ð, êîòîðàÿ íàõîäèòñÿ âáëèçè îñè CC′ (ïàðàêñèàëüíîå ïðèáëèæåíèå). Çäåñü α óãîë ïàäåíèÿ ýòîãî ëó÷à, β óãîë ïðåëîìëåíèÿ, F òî÷êà ïåðåñå÷åíèÿ ëó÷à ñ îñüþ ëèíçû, ò.å. ôîêóñ ëèíçû äëÿ ëó÷åé, áëèçêèõ ê îïòè÷åñêîé îñè. Ïîëàãàÿ óãëû α è β ìàëûìè, ò.å. ñ÷èòàÿ sin α = α è sin β = = β , èìååì α = n β (çàêîí ïðåëîìëåíèÿ ñâåòà) è OF/R = β α − β (òåîðåìà ñèíóñîâ äëÿ òðåóãîëüíèêà OPF), îòêóäà ïîëó÷àåì OF = R n − 1 . Ôîêóñíîå ðàññòîÿíèå ëèíçû, èçìåðåííîå îò åå âåðøèíû, ðàâíî > CF = R + R n −1 =R > n n −1 C C ≈ 3,1R . Ó íàøåé ëèíçû F = 2,6 ñì, ÷òî ñîîòâåòñòâóåò ðàäèóñó êðèâèçíû ëèíçû R = = 0,83 ñì. Èìåííî íà ðàññòîÿíèè ÷óòü Çàðÿæåííàÿ êàïëÿ Ïóñòü çàðÿæåííàÿ êàïëÿ íàõîäèòñÿ â ïîëå òÿæåñòè íà ãîðèçîíòàëüíîé ïîâåðõíîñòè, íå ñìà÷èâàåìîé âîäîé. Î÷åâèäíî, ÷òî åñëè ñèëà òÿæåñòè ñòðåìèòñÿ «ðàñïëþùèòü» êàïëþ, òî ñèëû ïîâåðõíîñòíîãî íàòÿæåíèÿ è ýëåêòðîñòàòè÷åñêîãî îòòàëêèâàíèÿ ñòðåìÿòñÿ, íàîáîðîò, «ðàñïðÿìèòü» åå, ñäåëàòü ñôåðè÷åñêîé. Êàê îöåíèòü âêëàä êàæäîé èç ñèë? Ïðè êàêîì ðàäèóñå êàïëÿ áóäåò ìàëî îòëè÷àòüñÿ îò øàðèêà? áîëüøå äþéìà îò âåðøèíû ëèíçû ïîä íåé è áûëà ñïðÿòàíà ôîòîãðàôèÿ, êîòîðàÿ «ïðîÿâèëàñü», êîãäà ìû ïîìåñòèëè ëèíçó â âîäó. Êàêèì îáðàçîì îêàçàëîñü âîçìîæíûì óâèäåòü ôîòîãðàôèþ ïîä ëèíçîé â âîäå? Äåëî â òîì, ÷òî â âîäå ïðåëîìëÿþùàÿ ñïîñîáíîñòü ëèíçû óìåíüøèëàñü è èç êîðîòêîôîêóñíîé ëèíçà ïðåâðàòèëàñü â äëèííîôîêóñíóþ. Äåéñòâèòåëüíî, êîýôôèöèåíò ïðåëîìëåíèÿ âîäû â âèäèìîé îáëàñòè ñïåêòðà ñîñòàâëÿåò nâ = 1,33 1,34, à îòíîñèòåëüíûé êîýôôèöèåíò ïðåëîìëåíèÿ îðãñòåêëà â âîäå ðàâåí nîòí = n nâ = 1,10 ± 0,01 . Ïîýòîìó íèæíåå ôîêóñíîå ðàññòîÿíèå íàøåé ëèíçû, çàëèòîé ñâåðõó âîäîé, îêàçàëîñü ðàâíûì Fâ = R nîòí nîòí − 1 = 11 , 0,1 R = 11R , åñëè ñ÷èòàòü, ÷òî ïîëóïðîñòðàíñòâî ïîä ëèíçîé ñîñòîèò èç îðãñòåêëà è ôîêóñíîå ðàññòîÿíèå èçìåðÿåòñÿ îò âåðøèíû ëèíçû. Òàêèì îáðàçîì, âîäà óâåëè÷èâàåò ôîêóñíîå ðàññòîÿíèå ëèíçû áîëåå ÷åì â 3,5 ðàçà, ÷òî îêàçûâàåòñÿ âïîëíå äîñòàòî÷íûì äëÿ íàáëþäåíèÿ ñïðÿòàííîãî ïîä ëèíçîé îáúåêòà. Èäåÿ ðàññìîòðåííîãî îïûòà î÷åíü ïðîñòà è ìîæåò áûòü èñïîëüçîâàíà â äðóãèõ ñëó÷àÿõ. Òàê, ëèíçó ìîæíî ñäåëàòü ìàòîâîé, ñòóïåí÷àòîé (ñî ñòóïåíüêàìè îò ðåçöà) èëè äàæå ãîôðèðîâàííîé. Èëè åùå ïðîùå â êà÷åñòâå ìàñêèðîâî÷íîãî ïîêðûòèÿ íåêîòîðîãî ïëîñêîãî îáúåêòà ìîæíî âçÿòü ìàòèðîâàííóþ ñâåðõó ïëàñòèíêó èç ïðîçðà÷íîãî ìàòåðèàëà, êîòîðàÿ â âîäå èëè äðóãîé ñïåöèàëüíîé æèäêîñòè ñòàíåò íà âèä ïî÷òè ãëàäêîé, ÷òî ïîçâîëèò íàáëþäàòü ñïðÿòàííûé ïîä ïëàñòèíêîé îáúåêò. Òàêàÿ îïòè÷åñêàÿ ìàñêèðîâêà è äåêîäèðîâêà îáúåêòà ñ ïîìîùüþ èçìåíåíèÿ ïîêàçàòåëÿ ïðåëîìëåíèÿ ñðåäû Èñïîëüçóåì ýíåðãåòè÷åñêèé ïîäõîä è çàïèøåì óñëîâèå ñôåðè÷íîñòè êàïëè â âèäå Wï + Wý ≥ Wò , ãäå Wï = σS = = 4 πσR 2 òàê íàçûâàåìàÿ ïîâåðõíîñòíàÿ ýíåðãèÿ (ñâÿçàííàÿ ñ ñèëàìè ïîâåðõíîñòíîãî íàòÿæåíèÿ), Wý = q 2 ?8πε RD = 2πε E R 0 2 3 0 ýëåêòðîñòàòè÷åñêàÿ ýíåðãèÿ, Wò = mgR = 4 πρgR 4 3 ýíåðãèÿ òÿãîòåíèÿ. Çäåñü σ êîýôôèöèåíò ïîâåðõíîñòíîãî íàòÿæåíèÿ âîäû, R ðàäèóñ êàïëè, Å íàïðÿæåííîñòü ýëåêòðîñòàòè÷åñêîãî ïîëÿ íà ïîâåðõíîñòè êàïëè, ρ ïëîòíîñòü âîäû. Ïîëó÷èëè ôàêòè÷åñêè êâàäðàòíîå C α R α β P n¾ O n > F C Ðèñ. 5 ïðåäñòàâëÿåò îïðåäåëåííûé ïðàêòè÷åñêèé èíòåðåñ.  çàêëþ÷åíèå íåñêîëüêî çàäà÷ äëÿ ñàìîñòîÿòåëüíîãî ðåøåíèÿ. 1. Ó ëèíçû, èçîáðàæåííîé íà ðèñóíêå 5, îïðåäåëèòå ôîêóñíîå ðàññòîÿíèå äëÿ ëó÷åé, ðàñïðîñòðàíÿþùèõñÿ âäîëü îïòè÷åñêîé îñè â íàïðàâëåíèè ââåðõ (âåðõíèé ôîêóñ). 2. Ïîêàæèòå, ÷òî ôîêóñíîå ðàññòîÿíèå îäíîðîäíîãî øàðà ðàäèóñîì R, ñäåëàííîãî èç ïðîçðà÷íîãî äèýëåêòðèêà ñ êîýôôèöèåíòîì ïðåëîìëåíèÿ n R 2−n (1 < n < 2), ðàâíî F = . 2 n −1 3. Øàð ðàäèóñîì R ñ êîýôôèöèåíòîì ïðåëîìëåíèÿ n1 íàõîäèòñÿ â ïëàñòèíêå òîëùèíîé 2R ñ êîýôôèöèåíòîì ïðåëîìëåíèÿ n2 ( n2 < n1 ). Îïðåäåëèòå ôîêóñíîå ðàññòîÿíèå øàðà ñ ïëàñòèíêîé ïðè íîðìàëüíîì ïàäåíèè ñâåòà íà ïëàñòèíêó. 4. Ïðèäóìàéòå, êàêèìè åùå îïòè÷åñêèìè ñïîñîáàìè ìîæíî ñäåëàòü âèäèìûì îáúåêò, «ñïðÿòàííûé» â ôîêàëüíîé ïëîñêîñòè ëèíçû. 5. Ïî÷åìó âîäà íå ïðîíèêàåò â çàçîð ìåæäó ëèíçîé è ïîäñòàâêîé (áëàãîäàðÿ ÷åìó â íàøåì îïûòå ôîòîãðàôèÿ îñòàåòñÿ âñåãäà ñóõîé)? > > C C íåðàâåíñòâî 4 πρgR4 , 3 îòêóäà íàõîäèì ðàäèóñ êàïëè 4πσR2 + 2πε 0E2 R3 ≥ 2 R≤ 3ε 0 E + 2 4 9 ε 0 E + 48 σρg . 4 ρg Ïîäñòàâëÿÿ ìàêñèìàëüíî âîçìîæíîå çíà÷åíèå íàïðÿæåííîñòè ýëåêòðîñòàòè÷åñêîãî ïîëÿ Å = 3 ⋅ 106 Â/ì (ïðè áîëüøåé íàïðÿæåííîñòè ïðîèçîéäåò ïðîáîé âîçäóõà), èìååì R ≤ 1,38 ñì. Äëÿ íåçàðÿæåííîé (Å = 0) êàïëè R ≤ 0,47 ñì. Çíà÷èò, çàðÿæåííàÿ êàïëÿ ñîõðàíÿåò ñôåðè÷åñêóþ ôîðìó ïðè âòðîå áîëüøåì ðàäèóñå. Â.Äðîçäîâ 45