Представление сигнала в базисе функций Уолша Лабораторная работа №1.1 Краткие теоретические сведения
реклама

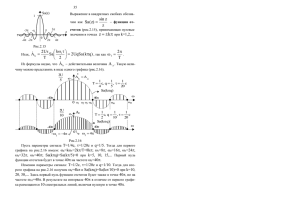
Лабораторная работа №1.1 Представление сигнала в базисе функций Уолша Краткие теоретические сведения Функциями Уолша назвывается семейство функций, образующих ортогональную систему, принимающих значения только 1 и −1 на всей области определения. В принципе функции Уолша могут быть представлены в непрерывной форме, но чаще их определяют как дискретные последовательности из 2n элементов. Группа из 2n функций Уолша образует матрицу Адамара. Функции Уолша получили широкое распространение в радиосвязи, где с их помощью осуществляется кодовое разделение каналов (CDMA), например, в таких стандартах сотовой связи, как IS-95, CDMA2000 или UMTS. Система функций Уолша является ортонормированным базисом и как следствие позволяет раскладывать сигналы произвольной формы в обобщённый ряд Фурье. Обозначение Пусть функция Уолша определена на интервале [0, T]; за пределами этого интервала функция периодически повторяется. Введём безразмерное время . Тогда функция Уолша под номером k обозначается как wal(k,θ). Нумерация функций зависит от метода упорядочения функций. Существует упорядочение по Уолшу, в этом случае функции обозначаются так, как описано выше. Также распространены упорядочения по Пэли (pal(p,θ)) и по Адамару (had(h,θ)). Относительно момента θ = 0 функции Уолша можно разделить на чётные и нечётные. Они обозначаются как и соответственно. Эти функции аналогичны тригонометрическим синусам и косинусам. Связь между этими функциями выражается следующим образом: Свойства Ортогональность Скалярное произведение двух разных функций Уолша равно нулю: Пример. Допустим, что n = 1, k = 3 (см. выше). Тогда, Мультипликативность Произведение двух функций Уолша даёт функцию Уолша. где — сложение по модулю 2 номеров в двоичной системе. Пример. Допустим, что n = 1, k = 3. Тогда, В результате умножения получим: Порядок выполнения работы 1. Задать сигнал, согласно варианту 1. 5. 6. 2. 3. 7. 4. 8. 9. 12. 13. 10. 11. 2.Задать первые 16 функций Уолша — от 0-го до 15-го порядка. Так, например, для функции четвёртого порядка на промежутке от 0 до 1 формула будет иметь вид: 1 3 5 7 Wal4 1 if 0 1 8 8 8 8 1 if 1 8 3 8 5 8 7 8 Графики этих функций приведены ниже. 1 Wal0( ) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.6 0.7 0.8 0.9 1 1 Wal1( ) 0 0.1 0.2 0.3 0.4 0.5 1 1 Wal1( ) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1 1 Wal2( ) 0 0.13 0.25 0.38 0.5 0.63 0.75 0.88 1 1 1 Wal3( ) 0 0.13 0.25 0.38 0.5 0.63 0.75 0.88 1 0.63 0.75 0.88 1 1 1 Wal4( ) 0 0.13 0.25 0.38 0.5 1 Wal5( ) 0 0.13 0.25 0.38 0.5 0.63 0.75 0.88 1 1 Wal6( ) 0 0.13 0.25 0.38 0.5 0.63 0.75 0.88 1 1 1 Wal7( ) 0 0.13 0.25 0.38 0.5 1 0.63 0.75 0.88 1 1 Wal8( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 0.56 0.63 0.69 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 1 1 Wal9( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 0.75 0.81 0.88 0.94 1 1 1 Wal10( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 1 1 Wal11( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 1 1 Wal12( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 1 1 Wal13( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 1 1 Wal14( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 1 1 Wal15( ) 0 0.063 0.13 0.19 0.25 0.31 0.38 0.44 0.5 1 0.56 0.63 0.69 0.75 0.81 0.88 0.94 1 3. Перемножить заданный сигнал с каждой из 16 функций Уолша. Построить графики S Wal0 , S Wal1 и т.д. 4. Построить «спектральную диаграмму», вида: 0.5 . Bn So 0 1 2 3 4 5 6 7 8 9 10 11 0.5 n где Bn находится по формуле 1 B S Wal n d n , а Wal n, в свою очередь, находится как 0 Wal0 Wal1 Wal2 Wal3 Wal4 Wal5 Wal6 Wal7 Wal Wal8 Wal9 Wal10 Wal11 Wal12 Wal13 Wal14 Wal15 5. Аппроксимировать сигнал по формуле Sa 15 Bn Wal n n 0 Построить на одном графике исходный и синтезированный сигналы: 12 13 14 15 2 . S( ) Sa( ) 0 0.2 0.4 0.6 0.8 2 6. Определить энергию сигнала и ошибку аппроксимации: 1 2 Ec S d Ec 0.477 Bn Ea 0.46 0 Ea 2 n Ec Ea Ec 0.017 0.035