статически неопределимой - Математика. Теоретическая
реклама
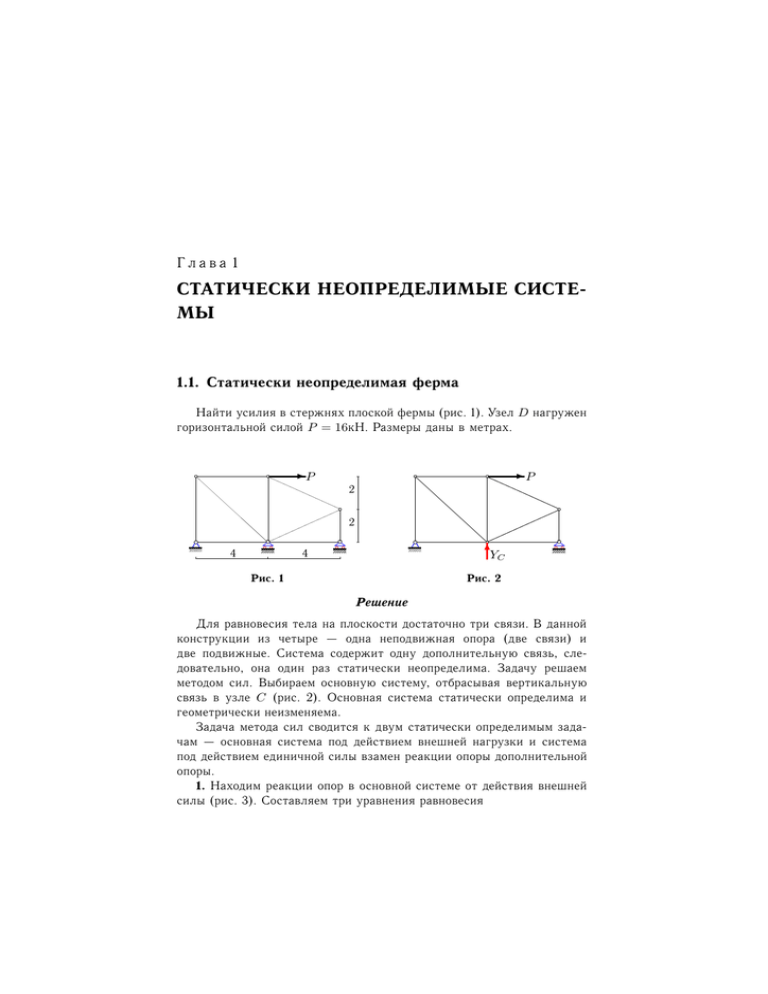
Глава 1 СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 1.1. Статически неопределимая ферма Найти усилия в стержнях плоской фермы (рис. 1). Узел D нагружен горизонтальной силой P = 16кН. Размеры даны в метрах. -P -P 2 2 4 6 YC 4 Рис. 1 Рис. 2 Решение Для равновесия тела на плоскости достаточно три связи. В данной конструкции из четыре — одна неподвижная опора (две связи) и две подвижные. Система содержит одну дополнительную связь, следовательно, она один раз статически неопределима. Задачу решаем методом сил. Выбираем основную систему, отбрасывая вертикальную связь в узле C (рис. 2). Основная система статически определима и геометрически неизменяема. Задача метода сил сводится к двум статически определимым задачам — основная система под действием внешней нагрузки и система под действием единичной силы взамен реакции опоры дополнительной опоры. 1. Находим реакции опор в основной системе от действия внешней силы (рис. 3). Составляем три уравнения равновесия 6 Статически неопределимые системы Раздел 1 P Xi = P MA = P MB = XA + P = 0, YB · 8 − P · 4 = 0, −YA · 8 − P · 4 = 0. -P 2 2 XA 6 YA 4 4 6 YB Решаем систему уравнений. Находим XA = −P = −12 кН, YA = −P/2 = −6 кН, YB = = P/2 = 6 кН. Рис. 3 Для проверки составляем сумму проекцию всех сил, действующих на ферму, на ось y: X Yi = YA + YB = 0. O1 RU1 R D1 XA- 6 YA U1 Рис. 4 Составляем два Находим усилия в стержнях фермы от действия сил в основной системе. Усилия O1 , U1 , D1 найдем по методу Риттера [3]. Рассекаем стержни первой панели вертикальным сечеRO1 нием (рис. 4). Находим точки Риттера (моментные точки) на пересечениях линий действия усилий в сечении. Таких точек две: RO1 , RU1 . уравнения моментов относительно точек Риттера P MRO1 = −O1 · 4 − YA · 4 = 0, P MRU 1 = U1 · 4 + XA · 4 = 0. (1.1) Усилие D1 в раскосе, для которого нет точки Риттера (усилия O1 , U1 параллельны), определяем из уравнения проекций на вертикальную ось X Yi = YA − D1 cos 45 = 0. (1.2) RO2 Y O2 RU2 D2 U2 6 YB Рис. 5 RD2 Рассекаем стержни второй панели вертикальным сечением (рис. 5). Находим точки Риттера: RO2 , RU2 , RD2 . 1.1. 7 Статически неопределимая ферма Составляем уравнения моментов P MRO2 = O2 · 4 sin γ + O2 · 2 cos γ + YB · 4 = 0, P MRU 2 = −U2 · 2 = 0, P MRD2 = D2 cos γ · 2 + D2 sin γ · 4 − YB · 4 = 0. (1.3) Усилия в вертикальных стержнях V1 , V2 , V3 методом Риттера найти нельзя. Нет сечений, рассекающих ферму на две части (части должны содержать хотя бы один стержень) и пересекающих эти стержни. Используем метод вырезания узлов. Вырезаем узлы A, B, D (рис. 7– 8), заменяя действие стержней их реакциями, направленными от узла к стержню. V V 61 63 O1 D V ?2 -P j O2 UXA1 A6 YA Рис. 6 U2 B 6 YB Рис. 7 Рис. 8 Составляем необходимы уравнения равновесия в проекциях. Потребуются только проекции на ось y: P A Y = V1 + YA = 0, P iB Y = V3 + YB = 0, (1.4) P iD Yi = −V2 − O2 sin γ = 0. Решения уравнений 1.1–1.4 заносим в столбец "SP k "таблицы 1 (в кН) Таблица 1 k 1 2 3 4 5 6 7 8 9 U1 U2 V1 V2 V3 D1 D2 O1 O2 SP k s1k Lk Sk 12 0 6 3 -6 -8.485 6.708 6 6.708 0 0 0.5 -0.25 0.5 -0.707 0.559 0.5 0.559 4 4 4 4 2 5.657 4.472 4 4.472 12 0 1.081 5.460 -10.919 -1.529 1.208 1.081 1.208 2. Прикладываем к ферме единичную силу по направлению реакции YC дополнительной опоры (рис. 9). Находим реакции опор в основной системе. Составляем три уравнения равновесия 8 Статически неопределимые системы P Xi = P MA = P MB = 2 2 XA 6 YA 4 6 1 4 Раздел 1 XA = 0, YB · 8 + 1 · 4 = 0, −YA · 8 − 1 · 4 = 0. Решаем систему уравнений. Находим XA = 0, YA = −0.5, YB = −0.5. 6 YB Рис. 9 Методом Риттера или методом вырезания узлов находим усилия в стержнях фермы от действия единичной силы. В данном случае уравнения равновесия 1.1–1.4 при этом не изменятся по форме. Изменятся лишь значения реакций опор. Кроме этого на рис. 6 не будет горизонтальной силы P . Решения заносим в столбец "s1k "таблицы 1. Для удобства вычислений в последний столбец таблицы запишем длины стержней. Записываем каноническую систему метода сил δ11 YC + ∆1P = 0, выражающую равенство нулю вертикального перемещения в точке C. Вычисляем коэффициенты канонической системы 1 X δ11 = Lk s21k = 8.327, EF k ∆1P 1 X Lk SP k s1k = 81.934. = EF k Решаем систему и получаем YC = −∆1P /δ11 = −9.839. Определяем реакции опор и усилия в стержнях статически неопределимой системы (P ) (1) XA = XA + XA YC = −12 (P ) + YA YC = −1.081 (P ) + YB YC = 10.919 YA = YA YB = YB (1) (1) Sk = SP k + s1k YC , k = 1..9. Результаты вычислений заносим в последний столбец таблицы 1. Список литературы 1. 2. 3. 4. 5. Говорухин В.Н., Цибулин В.Г. Компьютер в математическом исследовании. Учебный курс. — СПб.: Питер, 2001. Дьяконов В.П. MATLAB: учебный курс. — СПб.: Питер, 2001. Кирсанов М.Н. Решебник. Теоретическая механика/ Под ред. А. И. Кириллова. — М.: Физматлит, 2002. Матросов А. Maple 6. Решение задач высшей математики и механики. — СПб.: БХВ-Петербург, 2001. Очков В.Ф. Mathcad 12 для студентов и инженеров. — СПб.: БХВПетербург, 2005. Учебное издание КИРСАНОВ Михаил Николаевич Решебник Сопротивление материалов Редактор М. Б. Козинцева Оригинал-макет автора Оформление переплета:А.А.Логунов ЛР № 020528 от 05.06.97. Подписано в печать с оригинал-макета ***** Бумага офсетная. Усл.печ. л. 6,0 Тираж 5000 экз. Формат 60×84/16. Печать офсетная. Заказ









