Случайные величины Ω = {A 1,A2,...,An,...} (1) 0 P(A i) 1 (2) P(Ai +

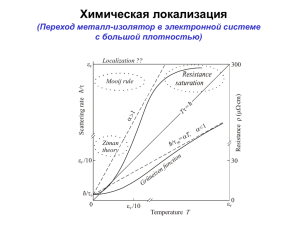
Случайные величины
Ω = {A1, A2, . . . , An, . . .}
(1)
0 6 P (Ai) 6 1
(2)
P (Ai + Aj ) = P (Ai) + P (Aj )
(3)
X
P (Ai) = 1
(4)
i
Pэмп = n/N
1
(5)
Функция распределения
F (x) = P (X 6 x)
(6)
0 6 F (x) 6 1
(7)
F (x1) 6 F (x2),
F (−∞) = 0,
2
для x1 < x2
(8)
F (∞) = 1
(9)
Плотность распределения вероятности
dF
w(x) =
dx
w(x)dx = P (x < X 6 x + dx)
w(x) > 0
Zx
F (x) =
w(ξ)dξ
∞
Z
(10)
(11)
(12)
(13)
−∞
w(x)dx = F (∞) = 1
−∞
3
(14)
Моменты случайной величины
∞
Z
f (x) =
f (x)w(x) dx
−∞
(15)
∞
Z
xnw(x) dx
mn = xn =
−∞
∞
Z
m1 = M (X) = mx = x =
∞
Z
xw(x) dx
−∞
4
(17)
−∞
x2w(x) dx
m2 = x2 =
(16)
(18)
∞
Z
(x − x)nw(x) dx
µn = (x − x)n =
(19)
−∞
∞
Z
µ2 = D(X) = σ2x =
(x − x)2w(x) dx
−∞
5
(20)
Равномерное распределение


x < x1 ;
0,
w(x) = 1/(x2 − x1), x1 6 x 6 x2;


0,
x > x2 .


x < x1 ;
0,
1
F (x) = xx−x
, x1 6 x 6 x2 ;
2 −x1


1,
x > x2 .
(21)
(22)
mx = 1/2(x1 + x2)
(23)
σ2x = (x2 − x1)2/12
(24)
6
Нормальное (гауссовское) распределение
2
1
(x − mx)
w(x) = p
exp −
(25)
2
2
2σx
2πσx
Zx
2
1
(ξ − mx)
p
exp −
dξ
(26)
F (x) =
2
2
2σ
2πσx
x
−∞
7
Системы случайных величин
X = {X1, X2, . . . , Xn}
F (x1, x2, . . . , xn) = P (X1 6 x1, . . . , Xn 6 xn)
x
Z1 xZn
F (x1, x2, . . . , xn) = . . . w(ξ1, . . . , ξn) dξ1 . . . dξn
(27)
(28)
(29)
−∞ −∞
w(x1, x2, . . . , xn) > 0
∞
Z
(30)
∞
Z
. . . w(x1, . . . , xn) dx1 . . . dxn = 1
−∞ −∞
8
(31)
∞
ZZ
x1 =
x1w(x1, x2) dx1dx2
(32)
x2w(x1, x2) dx1dx2
(33)
(x1 − x1)2w(x1, x2) dx1dx2
(34)
(x2 − x2)2w(x1, x2) dx1dx2
(35)
−∞
∞
ZZ
x2 =
−∞
∞
ZZ
σ21 =
−∞
∞
ZZ
σ22 =
−∞
9
Ковариация:
∞
ZZ
R12 = (x1 − x1)(x2 − x2)w(x1, x2) dx1dx2
(36)
−∞
Коэффициент корреляции:
r12 = R12/(σ1σ2)
Корреляционная матрица

1 r12
 r21 1
r=
 .. ..
rn1 rn2
10
(37)

. . . r1n
. . . r2n

. . . .. 
... 1
(38)
Многомерное нормальное распределение
w(x1, x2, . . . , xn) = s
1
(2π)n|r|
×
n
Q
i=1

n
σ2i

n
XX
1
(xi − mi) (xj − mj ) 
× exp −
Aij
2|r| i=1 j=1
σi
σj
(39)
где Aij — алгебраическое дополнение элемента rij
матрицы r
11