Химическая локализация
реклама
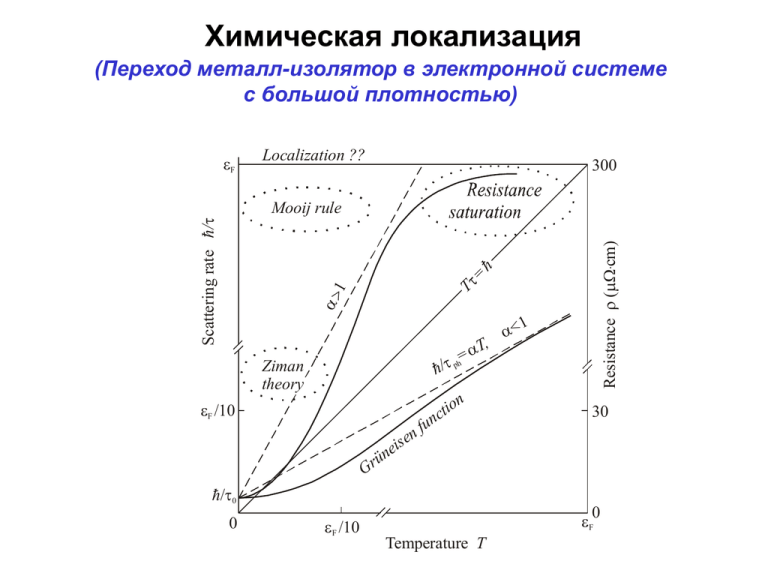
Химическая локализация (Переход металл-изолятор в электронной системе с большой плотностью) F Localization ?? 300 h = T, = h/ ph Ziman theory n tio c un f n i se e ün r G F /10 h/0 0 F /10 1 < Resistance (·cm) T 1 Scattering rate h/ Mooij rule 30 0 F Temperature T План лекции 103 InSb 1/3 nc aB = 0,26 1. Общие соображения 2. Интерметаллические соединения в двухкомпонентных расплавах Ge:Sb 102 aB (Å) CdS:In CdS:C Ge:P Ge:As Si:Sb Si:As Si:P GaP:Zn GaAs:Mn 10 3. Модель структурного беспорядка 4. Квазикристаллы WSe2:Ta Ar:Na WO3:Na 1 Ar:Cu 14 10 16 10 18 20 10 10 3 nc (cm ) 22 10 ? “Стандартные” металлы с P.P.Edwards and M.J.Sienko PRB 17, 2575 (1978) n 1 3 3A, n 4 10 22 cm 3 2 2 ne l e (k F l ) ~ k F l 2 n ~ k F3 as 1 F lmin ~ k , min В “стандартном” металле 2 e ~ kF n 1 3 3A, и max~ 200 ÷ 300 cm n 4 10 22 cm 3 ln (cAndW J 0 ) Переход Андерсона ln (cMottU J 0 ) Переход Мотта 1 aB n1/ 3 aB 2 m*e 2 , 1 J 1* H 2 d 3 r J 0 exp r12 aB интеграл перекрытия W U Mott transition point ? Двухкомпонентные расплавы 400 o 725 C W.F.Calaway, M.-L.Saboungi J.Phys.F 13, 1213 (1983) 200 14 100 5 10 20 500 oC 605 oC 625 oC 650 oC 40 60 at. % CsPb 6 80 Pb Rb-Pb 8 6 4 KSn NaSn LiSn 4 3 2 1 2 RbPb NaPb LiPb KPb 3 (10 cm) 2 CsSn (cm) 0 Na 7 12 Na-Pb (cm) (cm) 300 1 0 Rb 0 20 40 60 at. % 80 Pb 20 40 60 80 100 Sn concentration (at. %) 20 40 60 80 100 Pb concentration (at. %) R.Xu, T. de Longe, W. van der Lugt PRB 45, 12788 (1992) Двухкомпонентные расплавы Схема экспериментальной установки Подача металла К системе с инертным газом Трубка из непроводящего материала Шаровые краны 1, 2, 3 термопары L1 L4 восемь контактов для транспортных измерений в обоих коленах трубки Трубка из нержавеющей стали Атомные конфигурации ведут себя как квантовые ямы Внутри N электронов, но только 1 2 могут покинуть яму. Эффективная концентрация становится n /N вместо n. F Cs Pb Cs Li Pb 4 Pb Li Li Pb Pb Li Cs Маленькие атомы щелочного металла Большие атомы Cs Au Cs 600oC 104 Cs49Au51 103 Solid (cm) 1 (cm) 1 102 10 102 Cs-Au 10 Cs 20 40 60 at. % Liquid 1 500 600 o T ( C) 80 Au Cs-Au~ 3Cs-Cl F.Hensel Adv.Phys. 28, 555 (1979) 700 Модель Андерсона W можно представлять себе, как периодический набор одинаковых ям на фоне длиннопериодного случайного потенциала Модель структурного беспорядка (модель Лифшица): случайное расположение идентичных ям; нет длиннопериодного потенциала; уширение за счет квантового взаимодействия между ямами. V (r) v(r - R i ) Резонансные ямы Ri 3 1 r12 2 3 r23>r12 2 r23 4 r34 >r23 r12 1 r 2 J 0 exp 12 aB r12 n 1/ 3 Квазикристаллы 2 3 У малого числа n+m+p атомов 4 1 A nB m C p оптимальная локальная конфигурация может иметь ось симметрии 5 порядка Трансляционной симметрией можно пожертвовать Al70Pd22Mn8 Базисная локальная конфигурация содержит 3 оболочки с 51 атомом at. 98 at. 12 at. C.Janot Phys.Rev. B 53, 181 (1996) 30 at. Чем выше качество квазикристалла (определенное по рентгену), тем больше сопротивление. Это противоречит всему опыту физики металлов 51 at. Al70Pd22.5Re7.5 Отжиг делает Брегговские рефлексы острее, а сопротивление выше 0 5 15 Al70Pd22.5Re7.5 1.5 1 1 ln [(T)] cm 0.5 2 1/3 Т (K ) 1/3 0.5 1.0 0.6 0.9 1.2 0.4 0.8 1.2 1/2 1/2 T 1/4(K 1/4) T (K ) 10 K 1 0.5 0 1 (cm) 0 1.0 6 0 n 0.5 1 Tr o iti s an 1.0 3 12 1.5 cm 18 10 K = 1 1.0 T (K ) T (K ) 3 1 0.5 15 3 1 0.5 5 24 Т 1/2 (K1/2) 1 2 3 4 3 C.R.Wang, S.T.Lin, et al. J.Phys.Soc.Jpn. 67, 2383 (1998); 68, 3988 (1999); 69, 3356 (2000) Резюме 1. В электронных системах с высокой плотностью возможна двухступенчатая локализация: (a) большая часть носителей попадает в ловушки в “квазихимические квантовые точки;” (b) оставшаяся делокализованной меньшая часть претерпевает обычный переход металл-изолятор. 2. Два примера материалов с таким поведением электронов это бинарные металлические расплавы и квазикристаллы. 3. Описывая электронный транспорт в квазикристаллах, следует исходить не из плоских волн exp (ikr), а из локализованных волновых функций.