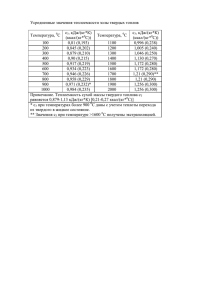
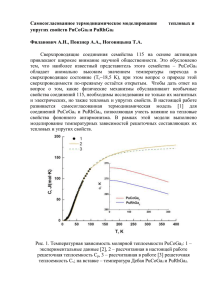
1.9 ТЕПЛОЕМКОСТЬ ИДЕАЛЬНЫХ ГАЗОВ

1.9 ТЕПЛОЕМКОСТЬ ИДЕАЛЬНЫХ ГАЗОВ
Теплоемкостью тела в каком-либо процессе изменения его
состояния называется количество подведённой (или отведённой)
теплоты, необходимое для повышения (или понижения) его
температуры на один градус.
В термодинамике газов различают
массовую теплоемкость с, кДж/(кг·град),
объемную теплоемкость с/ , кДж/(м3⋅град),
мольную теплоемкость µ c , кДж/(кмоль⋅град).
c=
µс
µс
; c/ =
;
µ
22, 4
c/ =
c
ϑ0 ,
где ϑ0 – удельный объем при нормальных условиях.
Теплота является функцией процесса:
для элементарного термодинамического процесса dq = du + dl . Как
было сказано выше, внутренняя энергия обладает полным
дифференциалом, а работа изменения объёма – нет. Значит, сумма
dq = du + dl не обладает свойствами полного дифференциала.
Поэтому понятие теплоемкости имеет смысл лишь в том случае,
когда задан характер процесса, в котором газу сообщается теплота.
Связь между теплотой процесса и температурой газа
q = f (T ) ,
Очевидно, что на различных участках такой
кривой одному и тому же изменению температуры
соответствуют различные количества
подведенной теплоты, поэтому и значения
теплоемкости на этих участках будут различными.
Вводят понятие о теплоемкости, средней в заданном интервале
температур от Т1 до Т2 (т.е. на участке 1–2).
T2
∆q
Cm =
∆T
T1
Значение истинной теплоемкости при заданной температуре:
 ∆q  dq
cист = lim 
=
∆T →0 ∆T  dT
Истинная теплоемкость математически выражается как первая
производная теплоты по температуре (при условии, что задан
характер процесса).
В термодинамике особо важную роль играют теплоемкость при
постоянном объеме
 ∂q 
cϑ =  
 ∂T ϑ
и теплоемкость при постоянном давлении
 ∂q 
cp =  
 ∂T  p
Связь между ними легко устанавливается из первого закона
термодинамики
dq = du + pdϑ
p2
q = i2 − i1 − ∫ ϑdp
или
p1
Если теплота подводится при постоянном объеме, то dϑ = 0 , а
следовательно,
 ∂u 
 ∂q 
cϑ = 

 =
∂
∂
T
T
ϑ
ϑ 

Если теплота подводится при постоянном давлении, то
 ∂u 
 ∂ϑ 
 ∂i 
cp = 
+
p
=





 ∂T  p
 ∂T  p  ∂T  p
В идеальном газе силы взаимодействия между молекулами
отсутствуют, а объём, который они занимают, также равен нулю, т.е.
внутренняя энергия u состоит только из кинетической энергии
движения молекул u = f (T ) и, значит, не зависит ни от объема, ни от
давления:
du
 ∂u 
 ∂u 
 =
 =

 ∂T ϑ  ∂T  p dT ,
ϑ=
RT
p
=>
R
 ∂ϑ 
=


∂
T

p p
Окончательно c p = cϑ + R
µ c p = µ cϑ + µ R
Молекулярно-кинетическая теория теплоемкости
Численные значения теплоемкости идеальных газов могут быть
получены из основного уравнения кинетической теории газов:
Умножая обе части этого уравнения на объем одного киломоля ϑµ ,
получаем
2
mω 2
pϑµ = ( nϑµ )
3
2
где N = nϑµ – число молекул в одном киломоле газа (число
Авогадро, 6,023⋅1026).
Если молекулы газа представить себе в виде материальных точек,
могущих совершать только поступательное движение, то внутренняя
энергия одного киломоля будет равна
−
u=
3
3
pϑµ = µ RT
2
2
Материальная точка имеет 3 степени свободы, следовательно, на
каждую из них в одном киломоле газа приходится внутренняя энергия,
1
µ RT
равная 2
.
При постоянном объеме подвод теплоты не вызывает совершения
работы газом, поэтому dq = ∆u , и мольная изохорная теплоёмкость:
−
u 3 + ϑвр
µ cϑ = =
µR
T
2
Мольная изобарная теплоёмкость:
µcp =
3 + ϑвр
2
µR + µR =
5 + ϑвр
2
µR
Зависимость теплоемкости от температуры
В точных расчетах, особенно при высоких температурах, кроме
энергии поступательного и вращательного движения молекул,
необходимо учитывать энергию колебательного движения атомов.
Характер процесса устанавливает
необходимую функциональную связь между
теплотой и температурой, а потому истинную
теплоемкость можно считать производной
теплоты по температуре
t2
q = ∫ cист dt
t1
Из графика видно, что теплота, затраченная на нагревание газа от
t1 до t2
q = пл0 − 5 − 2 − 3 − 0 − пл0 − 5 − 1 − 4 − 0 ,
или учитывая, что на оси ординат t=0
t2
t1
q = cm t 2 − cmt1
0
0
t
cm
Средние теплоемкости
сведены в таблицы теплоемкостей,
0
которые и используются для теплотехнических расчетов.
t2
t1
cm t 2 − cm t1
t2
0
cm = 0
.
t 2 − t1
t1
Теплоемкость газовых смесей
Чтобы вычислить теплоемкость газовой смеси по теплоемкостям ее
компонентов, необходимо знать массовый, объемный или мольный
состав этой смеси.
Если смесь задана массовым составом
cсм = m1c1 + m2 c2 + ..., кДж/(кг⋅град)
Если смесь задана объемным составом
/
сcм
= r1c1/ + r2 c2/ + ... , кДж/(кг⋅град)
Если смесь задана мольным составом, то принимаются те же
формулы, что и при задании ее объемным составом.